一、说明

机器学习在人工智能历史上扮演重要角色，然而，存在问题也不少。为了适应新时代和新任务，不做出重大改进是不可能的，本篇就一些突出问题和改进做出讨论。以便读者掌握未来的思路和方向。

二、机器学习历史回顾

6年前，机器学习的作用是弄清楚如何执行人们容易执行但难以正式描述的任务。在那个时候，在语音识别和物体检测等直观任务上重现人类的能力是积极研究的主要目标。尽管这些任务没有完全解决，但值得注意的是该领域的成就，这些成就对日常生活产生了直接影响。我们可以将自动驾驶和口语转录作为该技术的合法示例。

三、机器学习战场转移

然而，如今，人工智能的主要战场从最终用户需求转移到大型组织和治理的巨大需求。举个例子，昨天的挑战是识别用户面部以解锁手机。如今，执行人脸识别超过百万或十亿张人脸成为需要克服的新前沿。

这种新场景带来了新的技术挑战。事实上，由于 6 年旧模型的非线性计算成本，解决大量数据的复杂模式识别任务不仅仅是在庞大的后端基础设施上运行旧模型的问题。需要一个新的机器学习模型系列。

当然，这项技术已经可用，并且存在严重的隐私问题，道德和社会后果。在本系列文章中，我们将从头开始探讨这些主题，调查在最近的出版物和公共存储库中可以找到的内容。

希望越容易理解，就越容易决定如何将其用于好事。这从本文开始

四、用简单语言还原过去

简而言之，据说计算机程序可以学习其性能何时随着经验的提高而提高。这种体验是什么样的？

在人工智能算法方面，这种经验包括处理数据。对制作计算机程序感兴趣的研究领域称为机器学习。

事实上，在过去的二十年里，人工智能受到了机器学习进步的强烈影响。尽管那个时代ML中使用的核心算法并不新鲜，但研究人员在执行自然语言处理和计算机视觉等领域的复杂任务时显着提高了计算机的性能。

最常见的机器学习任务是模式识别（例如，在图像中查找人脸）。但是，还有其他任务类型，例如转录和数据生成。我们将在文章后面中讨论这些类型的任务。

五、训练计算机执行操作

机器学习的核心范式是使用数据来提供训练算法。 这种训练的输出是一个最终能够执行感兴趣的任务的模型。因此，训练算法不是静态定义/编码程序来执行某些操作，而是教导（拟合）模型以执行该操作。

5.1 神经网络的作用

最成功的机器学习模型之一（也许是最成功的一个）是人工神经网络，或者不久之后，ANN。尽管取得了成功，但直到2004年，ANN仅用于玩具应用程序，概念或小型独立场景。但是为什么？

使用旧 ANN 架构处理一个图像所花费的估计时间

使用高维数据（例如640x480图像）训练传统ANN的计算成本令人望而却步，即使使用现代计算机也根本不可行。这只有在深度学习的进步之后才会改变。

理解和使用香草神经网络仍然是必要的。我们将在下一篇文章中讨论经典ANN模型的细节

5.2 深度学习占据了现场

过去十年见证了深度学习模型的兴起。深度学习是算法和技术的保护伞，它利用空间和时间局部性来减少所需的模型参数数量。这种方法通常称为参数共享。

实际上，深度学习使神经网络能够/实用地执行复杂的高维数据任务，例如实时处理VGA，HD或4K图像。事实上，如果没有深度学习，我们都会被锁在90年代的世界里。

>我们将在下一篇文章中介绍卷积神经网络、递归神经网络和生成对抗网络等深度学习模型

在我们结束这个演讲之前，有一些非常重要的事情要提。

5.3 优化和正则化

机器学习有两个核心问题，即优化和正则化。

当您使用数据来训练模型时，您希望找到更适合手头数据的最佳模型。这是优化。这里的陷阱是，如果你在这个拟合上走得太远，你可能会得到一个无用的模型，只适用于该数据，一个过度拟合的模型。

像这样的模型会记住训练数据，而不是学习数据中的规律。

来自维基百科的过度拟合示例

过度拟合是建模错误。寻找避免过度拟合的方法称为 regularization。

强烈建议阅读下一篇文章，介绍过拟合和正则化的基础知识。

六、建模基础知识

如果世界今天重新启动，您必须了解哪些建模概念才能重新启动机器学习？

尽管有科学的努力，但不可能理解作用在物理或社会现象上的每一种力量。发生这种情况是由于三类限制：

理论无知：给定现象的关系和理论规律尚不完全清楚
实际无知：缺乏完整的观察，如事实、测量和实验读数
懒惰：作用于给定现象的全套力是如此巨大，以至于无法列出它们或精确计算它们的结果

机器学习使用函数近似来处理这样的场景。这些函数近似称为模型。

6.1 模型

在机器学习的上下文中，建模是通过训练过程找到有用模型的过程。

当模型在看不见的数据（即构建过程中未使用的数据）上表现良好时，模型就很有用。简而言之：

当然，我们希望摆脱欠拟合和超拟合的模型。让我们考虑以下合成方案，以便了解如何操作。

6.2 合成数据支持

合成数据是一种宝贵的资源。在将模型和算法应用于实际数据之前，可以更轻松地理解它们的行为。在这里和之后，我们将使用合成数据来深入了解机器学习建模的主要关注点。

让我们假设我们以某种方式知道控制所研究现象的生成源：

蓝线代表我们已经奇迹般地知道的源函数。这个特殊的函数是周期性正弦波函数f（x） = sin（x）。JavaScript 中生成此正弦数据的代码是：

const N = 91;
// generating a sequence 91 elements from 0 to 2π
const xs = [...Array(N).keys()].map(x => 2*Math.PI*x / (N - 1));
// generating f(x) = sin(x)
const signal = xs.map(x => Math.sin(x));

// sampling 20 random elements and adding a N(0, 0.4) gaussian error
const sampleSize = 20;
const sample = [...Array(N).keys()].sort(() => 0.5 - jStat.uniform.sample(0, 1)).slice(0, sampleSize).map(index => ({x: index, y: signal[index] + jStat.normal.sample(0.0, 0.4)}));

图表中的红叉是通过实验程序从真实现象中获得的测量值。请注意，由于噪声源不同，这些实验读数与源生成正弦函数并不完全共线性。

正态分布是此类噪声的良好表示。事实上，中心极限定理指出，自随机变量的总和是近似正态分布的。

在真实场景中，我们甚至不知道生成源信号的形状。通常我们只能访问实验数据：

在本文的其余部分，我们将找到方法来获得源生成信号的良好近似值，假设我们既不知道它的形状也不知道公式。

6.3 近似函数

粗略地说，训练算法旨在找到给定训练数据的近似函数（或模型）。为了检查它的运行情况，我们将训练数据设置为原始实验数据的 67%，将剩余的 33% 留作将来验证：

> 拆分训练集和验证集中的数据称为保留。常见的拆分百分比为 67%、80%、90% 和 99%。

为了使事情尽可能简单，在这个实验中，我们将使用简单的基本教科书模型：直线（也称为 1 次多项式）、三次多项式（三次曲线）等。因此，使用最小二乘法，我们可以找到以下近似值：

哪个模型更接近训练数据？检查图像，我们可以发现第 9 次多项式曲线几乎经过每个训练点，而其他曲线或多或少更近。但是，如何量化这种接近度？

回答这个问题的一个很好的替代方法是均方误差或 mse：

mse 是预测值 Ŷ 和观测值 Y 之间的平方差的平均值。预测值是模型猜测的值，而观测值是数据集中的原始值。对于我们特定的一维数据，MSE 的实现非常简单：

function mse(model, data) {
    let result = 0.0;
    for (let i = 0; i < data.length; ++i) {
      	const elem = data[i];
      	const x = elem.x;
        const y = elem.y;
        const y_hat = predict(x, model);
        const diff = y_hat - y;
        result += diff * diff;
    }
    return result / data.length;
}

对于像 mse 这样的错误指示器，越小越好。对训练数据应用 MSE 会导致：

基于这种性能，我们可以认为最好的模型是第9次多项式次近似。当然，这是一个错误的发现：将 mse 应用于验证数据可以公平地查看实际模型性能：

上图使用对数刻度！它清楚地表明，第 9 项式模型在验证数据上表现不佳——尽管它在训练数据上实现了高性能。换句话说，这张图显示的是第 9 个多项式模型遭受过拟合。

另一方面，线性模型在训练集和验证集中的性能都很低。这称为欠拟合。在实际实验中，线性和 9 度模型都应丢弃。

这里最重要的一课是：使用训练中未使用的数据评估模型。

现在，我们知道如何检测过度拟合的模型。但是，是什么让模型过度拟合？如何避免？

6.4 过度安装和安装不足的原因

过度拟合的常见原因是模型复杂性。我们可以将模型复杂性恢复为模型中自由参数的数量。在第 9 多项式的情况下，有 10 个自由参数来拟合数据。自由参数越多，越容易过度拟合。

艾因斯滕引文调查在这里

相反，参数很少的模型容易出现欠拟合。这是使用线性模型近似（非线性）正弦波函数的情况。

模型复杂性的选择是在建模阶段要做出的更重要的决定之一。在训练算法中自动执行此决策是机器学习中积极研究的来源。

减少自由参数的数量或影响通常称为 regularization。我们将在另一篇文章中详细讨论正则化。

6.5 过度拟合和欠拟合的其他来源

拟合不足和过度拟合还有其他原因，通常与数据质量有关。特别是，小数据是一个大问题，对欠拟合和过拟合都有很强的影响。

数据采集和准备过程是建模成功的关键。我们将在下一篇文章中讨论它。

过度/欠拟合的另一个原因是训练超参数的选择。本系列的下一篇文章将介绍训练过程。

6.6 最后，是什么让模型有用？

在我们之前的实验中，具有中间复杂度（第 3 和第 5 个）的模型在训练和验证性能之间显示出最佳平衡。这种平衡是模型选择的主要指标。

但是，当两个或多个不同的模型具有大致相同的性能时，在这种情况下会发生什么？很简单！选择最简单的一个！

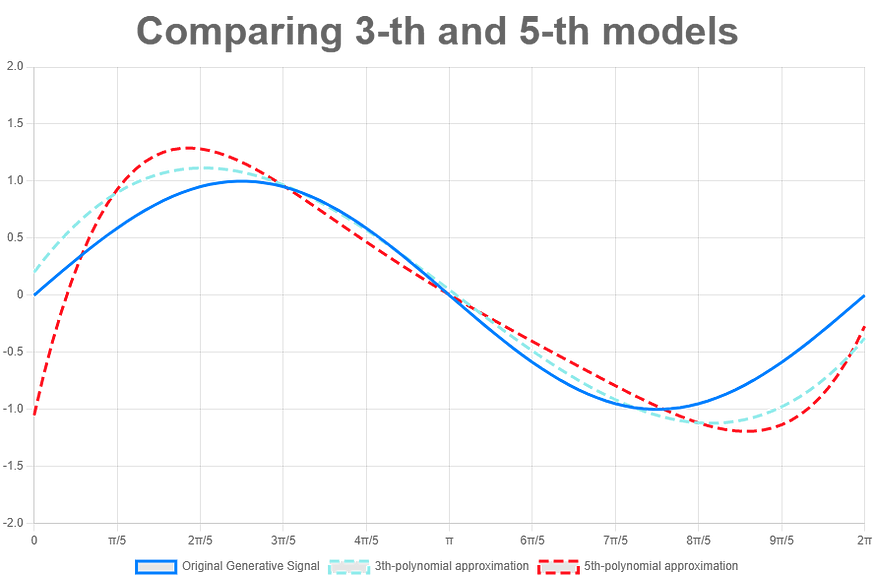
使用不太复杂的模型而不是更复杂的模型的论点被称为奥卡姆剃刀原理。查看前面的示例，我们发现 3 次和 5 次多项式模型的形状与原始源信号（蓝线）非常相似。因此，通过遵循奥卡姆剃刀原理，我们将选择第 3 个作为最终选择的模型。

> 在实时应用程序中，最简单的模型也是更快的模型。因此，对于两个性能相同的模型，最简单的模型始终是所选模型。

七、结论

在本文中，我们讨论了机器学习背景下建模的基本主题。使用合成场景和简单的学校级多项式函数来说明欠拟合和过度拟合等概念。在实际场景中，更复杂的模型取而代之，并使用适当的迭代训练算法。无论如何，这里讨论的核心建模主题，如训练和验证集，过度/欠拟合和模型复杂性也被发现并且同样有效。

八、代码

本文中使用的代码是用 JavaScript 编写的。您可以在此要点或使用下面的小提琴中找到它：

const ctx = document.getElementById('synthetic');
const N = 91;
const xs = [...Array(N).keys()].map(x => 2*Math.PI*x / (N - 1));

function mulberry32(a) {
    return function() {
      var t = a += 0x6D2B79F5;
      t = Math.imul(t ^ t >>> 15, t | 1);
      t ^= t + Math.imul(t ^ t >>> 7, t | 61);
      return ((t ^ t >>> 14) >>> 0) / 4294967296;
    }
}
// change seed to an arbitrary number
const seed = 1111;
jStat.setRandom(mulberry32(1111));

const signal = xs.map(x => Math.sin(x) );
const sampleSize = 20;
const sample = [...Array(N).keys()].sort(() => 0.5 - jStat.uniform.sample(0,1)).slice(0, sampleSize).map(index => ({x: index, y: signal[index] + jStat.normal.sample(0.0, 0.4)}));

sample.sort(() => 0.5 - jStat.uniform.sample(0,1));

const dataSplit = Math.round(sampleSize * 0.67);

const training_data = sample.slice(0, dataSplit);
const validation_data = sample.slice(dataSplit, sampleSize);

_labels = ["0", "π/5", "2π/5", "3π/5", "4π/5", "π", "6π/5", "7π/5", "8π/5", "9π/5", "2π"];

const x = [];
const y = [];

for (let i = 0; i < training_data.length; ++i) {

	const elem = training_data[i];
  x.push(xs[elem.x]);
  y.push(elem.y);

}

const order = 3;

function fit(x, y, order) {

  const xMatrix = [];
  const yMatrix = numeric.transpose([y]);
  let xTemp = [];

  for (let j=0; j<x.length; ++j) {
      xTemp = [];
      for(let i = 0; i <= order; ++i) {
          xTemp.push(Math.pow(x[j], i));
      }
      xMatrix.push(xTemp);
  }

  const xMatrixT = numeric.transpose(xMatrix);
  const dot1 = numeric.dot(xMatrixT, xMatrix);
  const dotInv = numeric.inv(dot1);
  const dot2 = numeric.dot(xMatrixT, yMatrix);
  const result = numeric.dot(dotInv, dot2);
  return result.flat(1);
}

function predict(x, coeffs) {

	let result = 0;
  let xx = 1;
  
  for (let i = 0; i < coeffs.length; ++i) {
  	result += xx*coeffs[i];
    xx *= x;
  }
	return result;
}

function generateModelData(x, y, order) {
  const model3 = fit(x, y, order);
  const result = [];
  for (let i = 0; i < xs.length; ++i) {
    result.push(predict(xs[i], model3));
  }
  return result;
}

const myChart = new Chart(ctx, {
    data: {
        labels: xs,
        datasets: [{
        
      			type: 'line',
            label: 'Original Generative Signal',
            pointRadius: 0,
            borderColor: 'rgb(0, 125, 255)',
            pointBackgroundColor: 'rgb(0, 125, 255)',
            data: signal
        },{
        
      			type: 'line',
            label: 'Linear approximation',
            pointRadius: 0,
            borderColor: 'rgb(88, 24, 69)',
            borderDash: [5, 3],
            data: generateModelData(x, y, 1)
            
        },{
        
      			type: 'line',
            label: 'Cubic Approximation',
            pointRadius: 0,
            borderColor: 'rgb(255, 87, 51)',
            data: generateModelData(x, y, 3)
        },{
        
      			type: 'line',
            label: '5th-degree polynomial approximation',
            pointRadius: 0,
            borderColor: 'rgb(165, 255, 51)',
            borderDash: [10, 5],
            data: generateModelData(x, y, 5)
        },{
        
      			type: 'line',
            label: '9th-degree polynomial approximation',
            pointRadius: 0,
            borderColor: 'rgb(123, 36, 28)',
            pointBackgroundColor: 'rgb(255, 0, 0)',
            borderDash: [10, 2],
            data: generateModelData(x, y, 9)
        },
        {
      			type: 'scatter',
            label: 'Training data',
            pointStyle: 'crossRot',
      			pointRadius: 10,
            borderColor: 'rgb(255, 128, 0)',
            data: Array(N).fill().map((element, index) => {
            	const v = training_data.find(elem => elem.x == index);
              if (v != undefined) {
            		return v.y;
              } else {
              	return null;
              }
            })
        }]
    },
    options: {
         plugins: {
         		legend: {
              
              position: 'bottom'
          	},
            title: {
                display: true,
                text: 'Polynomial regression',
                font: {
               		size: 48,
                	family: 'Arial'
              }
            }
        },
        scales: {
            x: {
                ticks: {
                		maxTicksLimit: _labels.length,
                    maxRotation: 0,
                    minRotation: 0,
                    callback: function(value, index, ticks) {
                        const factor = index * (_labels.length - 1);
                        let result = "";
                    		const n = N - 1;
                    		if (factor % n == 0){
                        	result = _labels[Math.ceil(factor / n)];
                        }
                        return result;
                    }
                }
            },
            y: {
                min: -2,
                max: 2,
            }
        }
    }
});

如果JavaScript不是你的首选语言，不用担心。将这些代码移植到不同的语言（如Python，Java或C++）并不难。

参考资料：查皮