一、什么是链表
链表是一种链状数据结构。简单来说,要存储的数据在内存中分别独立存放,它们之间通过某种方式相互关联。
如果我们使用C语言来实现链表,需要声明一个结构体作为链表的结点,结点之间使用指针关联。
二、单向链表的结构
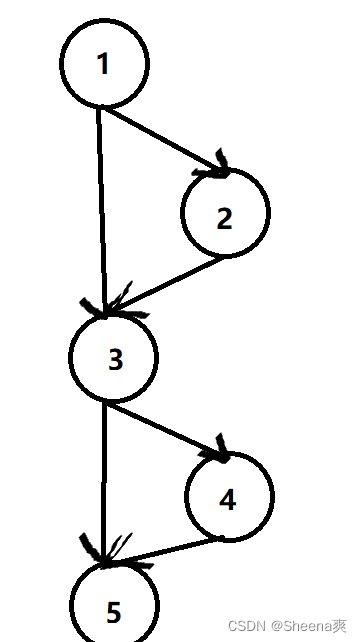
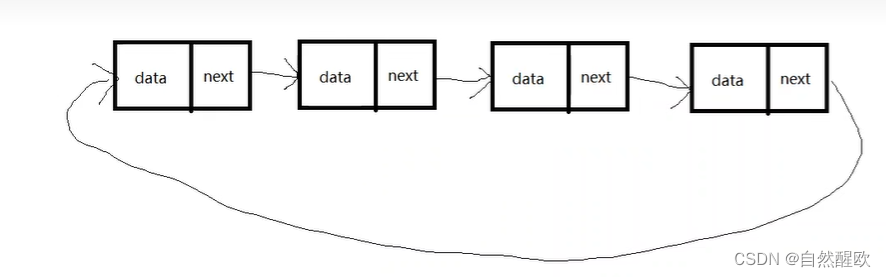
单向链表的每个结点内都有一个指针指向下一个结点,从而把所有结点串联起来。由于只有指向下一个结点的指针,这种结构是单向的,也就是前面的结点能找到后面的,但后面的结点找不到前面的,这就存在一定的问题。最后一个结点的指针是空指针,标识链表的尾结点。我们只需要获取链表头部的结点的地址,也就是指向链表头结点的指针,就能依次找到后面的每一个结点,从而管理整个链表。
说了这么多,链表的每个结点应该如何定义呢?很简单,每个结点应该有存储数据的变量(数据域)和指向下一个结点的指针(指针域)。我们假设存储的数据类型是int。
struct SListNode
{
int data;
struct SListNode* next;
};如果要存储其他类型的数据,为了修改方便,可以使用typedef,把int类型typedef成SLTDataType,从而方便修改存储类型。
typedef int SLTDataType;为了结构体使用方便,也typedef一下。
typedef struct SListNode
{
int data;
struct SListNode* next;
}SLTNode;三、打印、查找、销毁
这三个动作都要涉及一个知识点:如何遍历单链表?为了遍历单链表,我们需要获取指向链表头结点的指针(以下简称头指针)。假设我们已经获取了这个指针phead,每次我们都可以通过结点内的next指针找到下一个结点,直到找到尾结点,即next指针为NULL的结点。为此可以使用for循环遍历。
for (SLTNode* cur = phead; cur; cur = cur->next)
{
// ...
}打印每个结点的数据就简单了。
for (SLTNode* cur = phead; cur; cur = cur->next)
{
printf("%d->", cur->data);
}
printf("NULL\n");查找链表中的数据,也是依次遍历即可。
for (SLTNode* cur = phead; cur; cur = cur->next)
{
if (cur->data == x)
return cur;
}
return NULL; // 找不到如果要销毁链表,由于我们一般把结点都存储在栈上,所以使用free函数来释放空间。注意,如果结点的空间被释放,nextz指针就成为了野指针,就找不到下一个结点了。所以遍历时应该保存要释放的结点,先让cur指向next,再free掉保存的结点。
for (SLTNode* cur = phead; cur; )
{
SLTNode* del = cur;
cur = cur->next;
free(del);
}四、尾插、头插
如果要插入一个结点,我们需要先获取一个结点,前面说了,一般在堆上管理结点,所以使用malloc函数开辟结点。
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
if (newnode == NULL)
{
perror("malloc申请空间失败");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;有了newnode之后,需要把newnode和原链表关联起来。
先说尾插,我们需要找到尾结点,再让尾结点的next指向newnode。找尾结点非常简单,遍历链表即可,只不过当cur->next为NULL时就找到了。
SLTNode* tail = phead;
for (; tail->next; tail = tail->next)
{
;
}
tail->next = newnode;但是!上面的代码有一个严重的问题,你看出来了吗?代码中有tail->next的操作,也就是要对tail指针解引用,然而万一tail为NULL呢?tail为NULL说明phead为空,我们称链表phead为空的情况为空链表!也就是说一上来链表为空时尾插,就不能采取上面的方法。
该怎么办呢?你想想,此时链表里啥都没有,空空如也,只需要让phead指向newnode不就行了吗!
if (phead == NULL)
phead = newnode;一般来说了解到这就足够了。但是在实现数据结构的时候,我们一般把插入、删除数据等接口封装成函数,也就是说,我们要用一个函数实现尾插。函数的声明如下:
void SListPushBack(SLTNode* phead, int x);以上实现的完整代码如下:
void SListPushBack(SLTNode* phead, int x)
{
SLTNode* newnode = BuySListNode(x); // 假设已经把前面讲解的获取新结点的代码封装成函数
if (phead)
{
// 链表非空
// 找尾结点
SLTNode* tail = phead;
for (; tail->next; tail = tail->next)
{
;
}
tail->next = newnode;
}
else
{
// 空链表
phead = newnode;
}
}看出问题出在哪了吗?phead是函数的形参,对于phead=newnode这行代码,我们只是改变了形参,会影响外面的实参吗?不会!换句话说,我们把链表的头结点phead传给PushBack函数,函数内部对形参phead的修改不会影响外面的实参,而当PushBack函数调用结束后,函数内的形参phead会被销毁,这并没有完成尾插的任务!
为了完成任务,我们需要PushBack函数拿到phead的地址pphead,才能在函数内部通过解引用pphead的方式访问函数外的phead,从而修改phead。由于pphead是phead的地址,不可能为NULL,所以使用前都需要断言。
void SListPushBack(SLTNode** pphead, int x)
{
assert(pphead);
SLTNode* newnode = BuySListNode(x);
if (*pphead)
{
// 链表非空
// 找尾结点
SLTNode* tail = *pphead;
for (; tail->next; tail = tail->next)
{
;
}
tail->next = newnode;
}
else
{
// 空链表
*pphead = newnode;
}
}理解了尾插后,头插也就简单了。由于头插无论如何都会改变头结点,也就是无论如何都会改变phead,如果要在函数内部实现,就必须传二级指针pphead。
插入前的结构是:phead->头结点。插入后的结构是:phead->newnode ->原来的头结点。所以只需phead=newnode,并且newnode->next=原来的头结点(即phead)。但是两句话的顺序必须注意了,如果先把phead改了,就找不到原来的头结点了。你可以先思考一下两句顺序应该如何写呢?如果拿到的是phead的地址pphead,又应该如何写呢?
newnode->next = *pphead;
*pphead = newnode;思考一下,需不需要考虑链表为空的特殊情况?其实不用考虑,因为上述操作只对newnode解引用,而newnode不可能是NULL。如果还不放心,简单思考一下此时代码做的事情就明白了。*pphead为NULL,第一行代码使newnode的next指向了NULL,第二行代码使头指针指向了newnode。
五、尾删、头删
有了前面的铺垫,我们也很容易理解,如果要在函数内部实现删除操作,一定要传二级指针。这是因为,如果删除前只有一个结点,那么phead一定不为空,但删除之后链表为空,也就是phead为NULL,此时一定要改变phead,所以传参时需要传递phead的地址,即pphead。
删除前,必须要有一个准备工作,那就是断言一下链表非空。也就是phead不为NULL,即*pphead不为NULL。
assert(*pphead);先说头删,因为比较简单。只需要干掉头结点,然后让phead指向新的头结点即可。注意代码的先后顺序,如果头结点被释放,就找不到新的头结点了(即原头结点的next)。所以需要保存要释放的结点,让phead指向新的头结点后,再释放保存的结点。
SLTNode* del = *pphead;
*pphead = (*pphead)->next;
free(del);思考一下:需不需要考虑删除前链表只有1个结点的特殊情况?其实不需要,在该情况下以上代码仍然成立,只不过执行完后phead指向了NULL。
再来考虑下尾删。这是有一点挑战性的,如果你第一次学习链表,建议先自己实现一下,再来听我讲解。
我假设你已经尝试写了。思路还是那样,找到尾结点,再干掉它。就完了吗?No!你想想,新的尾结点是谁?是不是原来尾结点的前一个?那这个新的尾结点的next指针原来指向的结点被你干掉了,不就成野指针了吗?所以还要把这个指针置成NULL。也就是说,我们不仅需要找到尾结点并且把它干掉,还要找到尾结点的前一个结点,把这个结点的next置成NULL。
如果你一开始没想到这一点,现在再想想,如何找到尾结点的前一个结点呢?
由于单向链表每个结点只有next,没有prev(前驱指针,指向前一个结点的指针),所以只能向后找,不能向前找。找到尾结点的前一个结点tailPrev的代码如下,这个思路很巧妙,你能看懂吗?
SLTNode* tailPrev = *pphead;
for (; tailPrev->next->next; tailPrev = tailPrev->next)
{
;
}其实很简单,只需要想想尾结点前一个结点有什么特征,在满足这个特征时跳出循环就行了。尾结点的特征时tail->next=NULL,那尾结点前一个结点就要走两步才能走到NULL,即tailPrev->next->next=NULL,所以就有了上面的代码。
但是这个代码忽视了一个特殊情况,那就是如果链表只有一个结点,也就是phead->next=NULL,由于一开始tailPrev=phead,此时tailPrev->next->next=phead->next->next=NULL->next,对空指针解引用了,程序会崩溃!所以要对这个特殊情况单独处理,你想想怎么处理?很简单嘛!只有一个结点了,只需要free掉这个结点,再把phead置成NULL就行了!
六、插入删除的一般化
如果我们想要在任意位置插入或者删除呢?有了前面的铺垫,这个问题就不难了,无非是链接一些结点,或者是干掉一些结点。由于总会有改变phead的情况,所以以下均需要使用二级指针pphead。
先说插入。插入分两种情况,一种是在pos前面插入,一种是在pos后面插入,你觉得哪种更简单?如果是在前面插入,你怎么找到pos前面的结点?那还要从头结点一个一个往后找,多麻烦!所以肯定是在后面插入简单。
前插的思路:找pos前面的结点,需要prev从phead开始一个一个往后找,直到prev->next=pos就找到了。找到后,使得prev->next=newnode,newnode->next=pos就行了。思考一下需不需要考虑先后顺序?其实不用,因为prev,newnode,pos是3个独立的结点,相互之间互不影响。
SLTNode* prev = *pphead;
for (; prev->next != pos; prev = prev->next)
{
;
}
newnode->next = pos;
prev->next = newnode;需要考虑一种特殊情况,头部的插入需要改变phead,由于头插前面讲过,这里就不重复了。
后插就简单了,有了前面这么多的铺垫,你应该也可以写出来。注意代码的先后顺序!
newnode->next = pos->next;
pos->next = newnode;至于删除,也分为两种情况,分别是删除pos结点和删除pos之后的结点。想一想,哪种更简单?删除pos位置的结点,你还需要找到pos之前的结点,会更复杂一些。
删除pos位置的结点的思路:先找到pos之前的结点和pos之后的结点,连接这两个结点,干掉pos。注意代码的先后顺序!
SLTNode* prev = *pphead;
for (; prev->next != pos; prev = prev->next)
{
;
}
prev->next = pos->next;
free(pos);这里提一句,如果你不想总要考虑代码的先后顺序,可以先保存prev和next=pos->next,再让prev->next=next。
这里需要考虑一种特殊情况,如果phead=pos,即头删的情况,prev找到的就不是pos前面的结点了,此时需要单独处理,由于头删的情况前面已经讲解过,这里不再重复。
最后,删除pos之后结点就非常简单了。你可以自己写一下,然后对照后面的代码。
assert(pos->next); // pos后至少有1个结点
SLTNode* del = pos->next;
pos->next = del->next;
free(del);你是否考虑了对pos->next的断言呢?如果没考虑到,请好好反省一下。删除pos后面的结点,就说明了pos后面必须有结点!也就是pos->next不为NULL!
七、总结
单向链表虽然结构很简单,但使用起来可真麻烦啊。所以这种结构是有一定缺陷的。事实上,这种链表结构的全称是单向+不循环+不带头链表,具有一定的局限性。