LeetCode 16. 最接近的三数之和（中等）

【题目描述】

给你一个长度为 n 的整数数组 nums 和一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。

【示例1】

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

【示例2】

输入：nums = [0,0,0], target = 1
输出：0

【提示】

$3\le nums.length\le 1000$
$-1000\le nums[i]\le 1000$
$-10^4\le target\le 10^4$

【分析】

---

和第15题相似，和 target 最接近的数可能是大于等于 target 的最小的数，也可能是小于等于 target 的最大的数。前者和第15题一样，枚举指针 $i$，然后用双指针 $j$ 和 $k$ 求出大于等于 target 的最小的数。由于我们之前的实现方式是将 $k$ 从右向左移动，找到 nums[i] + nums[j] + nums[k] >= target 的最小的 $k$，因此我们可以得出 nums[i] + nums[j] + nums[k - 1] < target 且 $k-1$ 是满足该式的最大的 $k$（需要注意保证 $k-1\ne j$）。

---

【代码】

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        pair<int, int> res(INT_MAX, 0);
        for (int i = 0; i < nums.size(); i++)
        {
            for (int j = i + 1, k = nums.size() - 1; j < k; j++)
            {
                while (j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= target) k--;
                int s1 = nums[i] + nums[j] + nums[k], s2 = nums[i] + nums[j] + nums[k - 1];
                res = min(res, make_pair(abs(s1 - target), s1));  // 不一定会大于等于0，因此要用abs
                if (j < k - 1)  // 确保j和k-1不是一样的才能使用nums[k-1]
                    res = min(res, make_pair(target - s2, s2));  // 一定小于0
            }
        }
        return res.second;
    }
};

LeetCode 17. 电话号码的字母组合（中等）

【题目描述】

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

【示例1】

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

【示例2】

输入：digits = ""
输出：[]

【示例3】

输入：digits = "2"
输出：["a","b","c"]

【提示】

$0\le digits.length\le 4$
digits[i] 是范围 ['2', '9'] 的一个数字。

【分析】

---

直接 DFS 爆搜即可。

---

【Python代码】

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        d2str = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
        res = []
    
        def dfs(digits: str, u: int, now: str):
            if u == len(digits):
                res.append(now)
                return
            for c in d2str[int(digits[u])]:
                dfs(digits, u + 1, now + c)

        dfs(digits, 0, '')
        return [] if not digits else res

LeetCode 18. 四数之和（中等）

【题目描述】

给你一个由 n 个整数组成的数组 nums，和一个目标值 target。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]]（若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按任意顺序返回答案 。

【示例1】

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

【示例2】

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

【提示】

$1\le nums.length\le 200$
$-10^9\le nums[i]\le 10^9$
$-10^9\le target\le 10^9$

【分析】

---

和第15题一样，暴力枚举四个数时间复杂度为 $O(n^4)$，使用双指针算法可以优化成 $O(n^3)$。需要注意本题四个数相加可能会溢出。

---

【代码】

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int i = 0; i < nums.size(); i++)
            if (i && nums[i] == nums[i - 1]) continue;
            else for (int j = i + 1; j < nums.size(); j++)
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                else for (int k = j + 1, u = nums.size() - 1; k < u; k++)
                {
                    if (k > j + 1 && nums[k] == nums[k - 1]) continue;
                    while (k < u - 1 && (long long)nums[i] + nums[j] + nums[k] + nums[u - 1] >= target) u--;
                    if ((long long)nums[i] + nums[j] + nums[k] + nums[u] == target)
                        res.push_back({ nums[i], nums[j], nums[k], nums[u] });
                }
        return res;
    }
};

LeetCode 19. 删除链表的倒数第N个节点（中等）

【题目描述】

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

【示例1】

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

【示例2】

输入：head = [1], n = 1
输出：[]

【示例3】

输入：head = [1,2], n = 1
输出：[1]

【提示】

$1\le 结点数目\le 30$
$0\le Node.val\le 100$
$1\le n\le 结点数目$

【分析】

---

先扫描一遍链表，求出链表长度 $len$，那么我们再扫描一遍找到倒数第 $n+1$ 个结点，也就是正数第 $len-n$ 个结点（如果使用了虚拟头结点则为 $len-1-n$），将其 next 指针指向 next->next 即可。

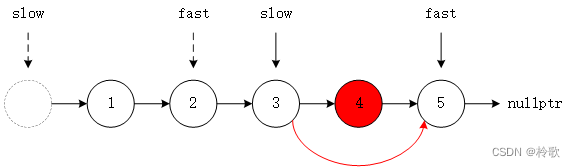
本题还可以使用快慢指针，如下图所示，我们设置两个间隔为 $n$ 的指针，在前面的记作 fast，后面的记作 slow，将两个指针一起移动，当 fast 的下一个结点为空时，slow 刚好走到倒数第 $n+1$ 个结点：

---

【代码】

【遍历求长度方法】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(-1);  // 凡是可能影响头结点的操作都先建一个虚拟头结点
        dummy->next = head;
        int len = 0;  // 链表总长度，包括虚拟头结点
        for (ListNode* p = dummy; p; p = p->next) len++;
        // 需要找到倒数第n-1个结点，由于有虚拟头结点，也就是正数第len-n-1个结点
        ListNode* cur = dummy;
        for (int i = 0; i < len - n - 1; i++) cur = cur->next;
        cur->next = cur->next->next;
        return dummy->next;
    }
};

【快慢指针方法】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(-1);  // 凡是可能影响头结点的操作都先建一个虚拟头结点
        dummy->next = head;
        ListNode* fast = dummy;
        ListNode* slow = dummy;
        while (n--) fast = fast->next;
        while (fast->next) slow = slow->next, fast = fast->next;
        slow->next = slow->next->next;
        return dummy->next;
    }
};

LeetCode 20. 有效的括号（简单）

【题目描述】

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 每个右括号都有一个对应的相同类型的左括号。

【示例1】

输入：s = "()"
输出：true

【示例2】

输入：s = "()[]{}"
输出：true

【示例3】

输入：s = "(]"
输出：false

【提示】

$1\le s.length\le 10^4$
s 仅由括号 '()[]{}' 组成

【分析】

---

经典括号问题，使用栈即可轻松解决，遇到左括号时入栈，遇到右括号时判断和栈顶括号是否匹配，匹配则将栈顶括号弹出。判断左右括号是否匹配可以用 ASCII 码来判断，这三对括号的左右括号相减之差最多为2。

---

【代码】

class Solution {
public:
    bool isValid(string s) {
        stack<char> stk;
        for (char c: s)
            if (c == '(' || c == '[' || c == '{') stk.push(c);
            else
                if (stk.size() && abs(stk.top() - c) < 5) stk.pop();  // 左右括号的ASCII码差值不超过2
                else return false;
        return stk.empty();  // 如果最后栈为空说明全部匹配，否则说明还有左括号为匹配
    }
};