题目分析

首先我们来分析一下本题的思路

看到题目中给出的示例

题目的意思很简单，就是将给到的数字去做一个组合，然后看看这三条边是否可以构成三角形。那判断的方法不用我说，相信大家如果读过小学的话应该都明白的，即三角形两边之和大于第三边则可以构成三角形

其实对于三角形的判断我们无需去判别三次，而是可以进行取巧👇

看到这里，我们可以去找出三个数中较大的那个数，然后只需去比较a + b > c即可，而对于a + c > b与b + c > a则不用去进行一个比较，因为此时[c]已经是最大的了，那再去加上a或者b的话一定会更大，所以无需去做比较
不过呢，这需要我们先找出最大的那个数，即要去做一个排序的操作进行优化

上面的这种思路对我们本题的解法很有帮助，望读者先行理解

讲解算法原理

然后我们根据上面的思路来分析一下本题的算法原理

暴力枚举

首先的话第一种，大家都能想到的就是【暴力枚举】，下面的话我写了一手伪代码，也就是通过三层的for循环，去一一进行枚举的操作。不过呢这很明显，时间复杂度为 $O(n^3)$ 一定会造成超时。

for(int i = 0;i < n; ++i)
{
    for(int j = i + 1;j < n; ++j)
    {
        for(int k = j + 1;k < n; ++k)
        {
            check(nums[i], nums[j], nums[k]);
        }
    }
}

我们可以来看一下运行后的结果

再来试着分析一下复杂度：

对于check()函数而言，如果我们还是使用上面判断三次的方式来看三条边是否可以构成三角形，那么最终因为外层的循环就会使得时间复杂度到达 $3O(n^3)$ ；
但是呢，如果我们使用的是取巧的办法，那需要先去使用【sort】做一个排序。只判断一次的话最终的时间复杂度为 $O(NlogN + N^3)$
那么后者一定是要比前者的复杂度来得低的，所以我们要考虑到换一种解法

利用单调性，结合双指针进行求解

接下去我就来介绍一下【双指针】这种解法

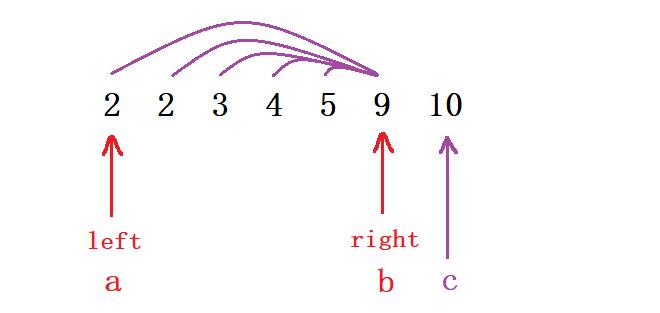
首先的话，上面说到过了，我们需要将整个数据先去做一个优化，使其呈现升序的样子，接下去呢我们要先拿到这个最大的数作为[c]；然后呢我们拿左指针left从左向右进行遍历，拿右指针right从右往左开始遍历
那我们现在看到a + b = 11 > c，那么就可以利用我们上面所介绍的这种思想，无需再去多判断

因为我们在一开始做了优化，数据是呈现升序排列的。例如像下面这里2 + 9、3 + 9、4 + 9等等这些都是要比10要来得大的，那其实我们根本无需再去判断这些数据，从【2】~【5】这5组数据均可以组成三角形，那此时如果我们要得到这个5的话只需要让right - left即可
那既然前面的数据都是与9进行结合，那这个9的话我们就使用完了，接下去让right--进行下一个数据的判断即可

接下去我们再来看第二种，此时我们可以看到2 + 5 = 7 < 10，那么此时我们可以继续去观察从【2】~【5】的这一堆数，它们一定是比5来得小的，那我们也无需再去多做比较了，对于这个【2】来说我们就可以舍弃了

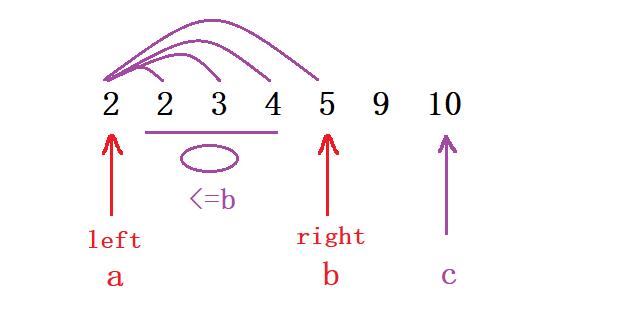
所以我们在来总结一下上面这种解法

先固定最大的数
在最大数的左区间内，使用双指针算法，快速统计出符合要求的三元组个数

复杂度

时间复杂度:

来说一下双指针这种解法的时间复杂度, 首先的话我们要在N个数内找到那个最大的数，然后的话还要使用【双指针】去遍历从0 ~ n - 1这N - 1个数，那么时间复杂度即为 $O(N^2)$

空间复杂度:

对于空间复杂度来说，没有去开辟任何的空间，所以为 $O (1)$

Code

来展示一下最终的代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        // 1.优化
        sort(nums.begin(), nums.end());

        // 2.利用双指针解决问题
        int ret = 0, n = nums.size();
        for(int i = n - 1; i >= 2; --i)     // 先固定最大的数
        {
            // a : nums[left]
            // b : nums[right]
            // c : nums[i]
            int left = 0, right = i - 1;
            while(left < right)
            {
                if(nums[left] + nums[right] > nums[i])
                {
                    ret += right - left;
                    right--;
                }
                else
                {
                    left++;
                }
            }
        }
        return ret;
    }
};