文章目录
- 特征值特征向量
- 补充一点关于正交标准化和相似对角化的理解
- 为什么要正交规范化呢?
- 相似对角化
- 为什么要相似对角化捏
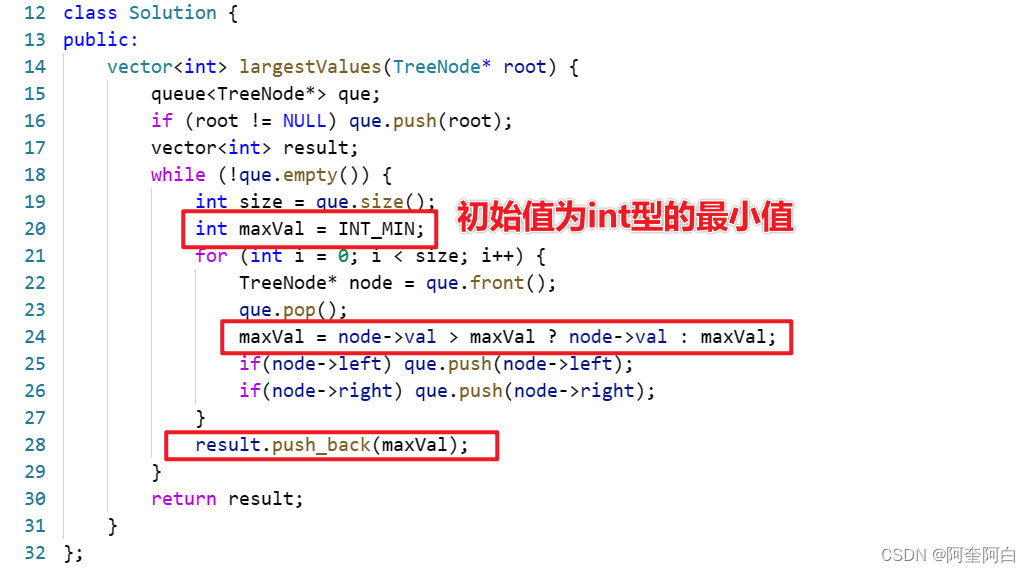
特征值特征向量
一些收集到的资料
资料一
迷惑很久,终于想通。 其实是一种数据的处理方法,可以简化数据。矩阵乘特征向量就是在其方向的投影。这点类似于向量点积既是投影。
通过求特征值和向量,把矩阵数据投影在一个正交的空间,而且投影的大小就是特征值。这样就直观体现了数据的基本特征。
最大特征值并不是说数据在所有方向的投影的最大值,而仅限于正交空间的某一方向。 至于为什么求出来的特征向量是正交的,可以证明。
有没有其他的正交空间,一般矩阵,满足满秩,只有一个这样的空间。
会不会有更好的空间来体现数据的特征,一般来说,正交空间就很好,不排除特殊应用需要非正交的空间,可能会更好。
我自己的理解:
特征值、特征向量最初的来源公式
A
α
=
λ
α
A\alpha=\lambda\alpha
Aα=λα
也就是说特征值和特征向量是针对变换矩阵A的,物理意义是对特征向量实施变换A以后,特征向量的方向不发生改变,只是大小进行了放缩,二维空间中,放缩的倍数就是 λ \lambda λ。
进一步的理解,特征向量不只一个,所有的这些特征向量组成一个特征空间,一个什么样子的特征空间呢?
一个通过变换矩阵A变换成到的特征空间S。对向量实施变换A就可以把向量变换到这个特征空间S。
我们如何感知和描述这个特征空间S呢?
参考基础解系,我们用一组线性无关的向量来标志这个向量空间,这个空间的所有向量都是这一组线性无关的向量的线性组合,可以称这一组向量为基向量。
比较标准的定义在这里:向量空间的基是它的一个特殊的子集,基的元素称为基向量。 向量空间中任意一个元素,都可以唯一地表示成基向量的线性组合。
以二维坐标系为例,任何一组不平行的向量(不包括0向量)都可以表征这个空间,我们最常用的基向量是
(
1
,
0
)
,
(
0
,
1
)
(1,0),(0,1)
(1,0),(0,1)。
回到上文中说的通过变换矩阵A变换到的特征空间S,A的特征向量就是这个特征空间的一组向量基,A的不同特征值对应的特征向量线性无关。A的特征向量组就能标志到特征空间S。
补充一点关于正交标准化和相似对角化的理解
为什么要正交规范化呢?
注意哈,这里的正交规范化的作用对象是所有向量空间的向量基,不局限于通A的特征向量构成的向量基。
正交:两向量正交内积=0
规范:向量的模为1
正交规范化的优点:求投影方便,也就是求某个向量基上的分量,比如在二维坐标系里面,求x轴和y轴分量
向量
α
1
\alpha1
α1在
α
2
\alpha2
α2上的投影
(
α
1
,
α
2
)
(
α
1
,
α
1
)
α
1
\frac{(\alpha1,\alpha2)}{(\alpha1,\alpha1)}\alpha1
(α1,α1)(α1,α2)α1
如果
α
1
\alpha1
α1是单位向量,那么
(
α
1
,
α
1
)
=
1
(\alpha1,\alpha1)=1
(α1,α1)=1,投影就是
(
α
1
,
α
2
)
⋅
α
1
(\alpha1,\alpha2)\cdot\alpha1
(α1,α2)⋅α1
向量 α 2 \alpha2 α2与单位向量的内积(投影大小)再乘以单位向量(投影方向)
相似对角化
为什么要相似对角化捏
为什么要提到相似对角化呢?因为对角化的过程又又又用到特征向量那一套玩意了,感觉线性代数学习过程中的各种理论你中有我,我中有你,缠绕的可太多了。
相似对角化可以简化矩阵的表达形式,将变换矩阵A对角化以后,变换不就简单许多了么?

是捏,好哎!但是对角化之后这个变换不就不是原来的变换了么?尽管映射到同一个特征空间,但是这个映射关系显然发生变化了呀。
这里就要去深入理解相似对角化了,相似对角化,原矩阵和对角矩阵必然是相似的,那么什么是相似呢?相似具有怎样的意义和性质呢?
(挖个坑吧,一篇博文太臃肿了,相似对角化新开一篇博文吧,我再理解理解)