题目

方法一：递归

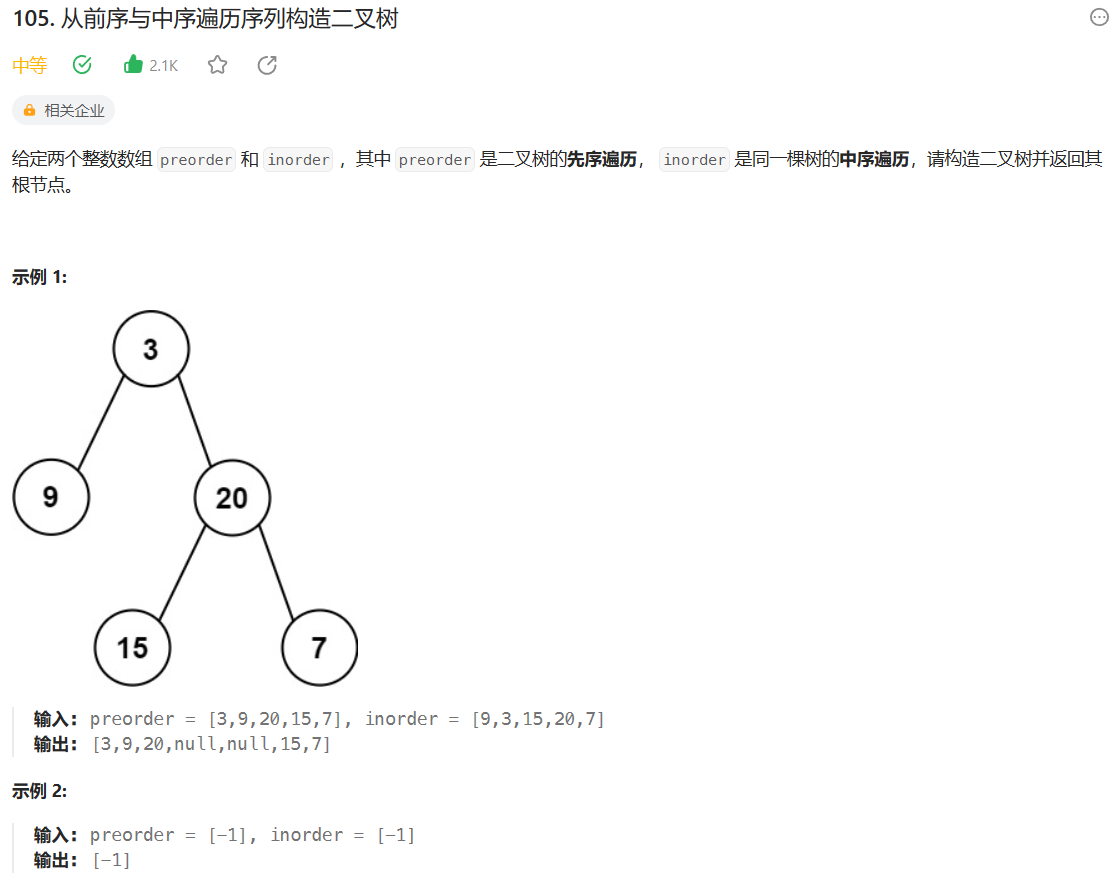
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
首先根据 preorder 找到根节点是 3
    
然后根据根节点将 inorder 分成左子树和右子树
左子树
inorder [9]

右子树
inorder [15,20,7]

这时候3是根节点  
3的左子树为如下
preorder[9] 

3的右子树为如下

preorder[20 15 7] 


现在我们只需要构造左子树和右子树即可，成功把大问题化成了小问题
然后重复上边的步骤继续划分，直到 preorder 空，返回 null 即可

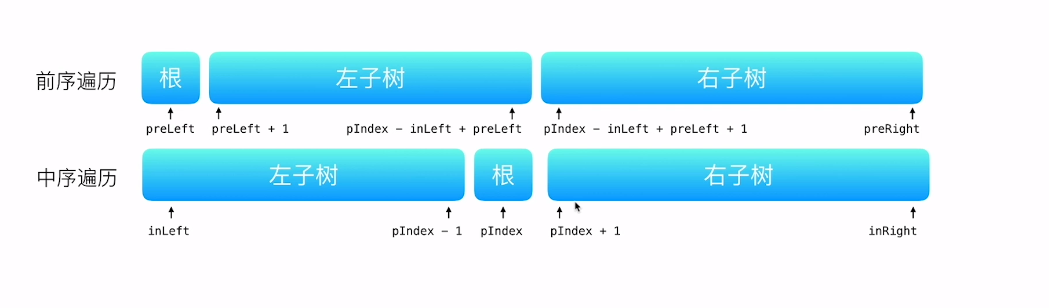
解题的关键在与找根节点和 左子树和右子树在前序遍历数组的范围，一步步找出根节点，然后划分出左右子树，然后让根节点指向左右子树，然后又对左右子树左重复动作

这个根据前序遍历的第一个节点（根节点）去中序遍历中找左右子树的范围，可以根据前序遍历的根节点值循环去中序遍历中找，因为题目保证节点不存在重复，所以可以根据中序遍历维护一个节点和下标的哈希表，这个前序遍历的根节点，可以轻松的找到中序遍历的根节点，从而在前序遍历中确定左右子树的范围

1. 根据中序遍历维护一个key为节点，value为下标的哈希表
2. 根据前序遍历的第一个节点（也就是根节点）去中序遍历哈希表找根节点
3. 再根据哈希表中找到的根节点，在中序遍历找到左子树的区间
4. 再根据这个区间，去前序遍历找到左子树的范围，以及右子树的范围
5. 新建根节点，指向待处理的左子树和右子树（递归）

// 方法一 ： 递归+哈希(到中序遍历数组中找 根节点值  然后判断出左右子树，再根据前序构建树)
    Map<Integer,Integer> inorderMap = new  HashMap<>(); //记录中序遍历节点与数组下标的映射关系
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //中序遍历数组下标映射map构造
        for(int i = 0 ; i<inorder.length;i++){
            inorderMap.put(inorder[i],i);
        }
        //构建树            前序数组  前序数组起始位置       前序数组末尾位置   中序数组起始位置       
        return myBuildTree(preorder,     0,               preorder.length - 1,                0        );
    }

      public TreeNode myBuildTree(int[] preorder, int prebegin , int preend,int inbegin) {
          if ( prebegin > preend) {
            return null;
        }
          int preorder_root = prebegin;  // 前序遍历中的第一个节点就是根节点
          int preindex = inorderMap.get(preorder[preorder_root]); // 在中序遍历中定位根节点

      
          TreeNode root = new TreeNode(preorder[preorder_root]);    // 先把根节点建立出来

          int size_left_subtree = preindex - 1 -inbegin; // 得到左子树中的节点数目

            // 递归地构造左子树，并连接到根节点
           // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素

            root.left = myBuildTree(preorder,prebegin +1,prebegin+1 + size_left_subtree,inbegin);

            // 递归地构造右子树，并连接到根节点
          // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素

            root.right = myBuildTree(preorder,prebegin+1 + size_left_subtree+1,preend,preindex+1);

          
          return root;
      }