【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
不可否认,slam中的有一部分内容来自于数学。但是,我们在学习使用的过程中,也不用纠结于整个数学的推导过程,能正确使用数学结论也是可以的。有能力的同学,按照书本提示的方法,自己推导一下,也无可厚非。实在觉得麻烦,可以暂时先放下,或者用的比较熟练了,再来查看相关的推导原理也可以。和那些复杂的高维矩阵运算、优化算法相比,有一些基本的数学和规则,可能大家在日常处理中遇到的机会更大,这里不妨总结一下。
1、浮点数
过去我们自己编写web前后端、或者写os、db的时候,遇到浮点数的机会并不多。即使遇到,也是简单的加减法。但是slam学习中,大量的操作都是浮点数。既然是浮点数,那么就离不开比较、除法、滤波、平方根这些计算。
1.1 数值比较
既然做浮点运算,那么数值比较肯定是少不了的。这个时候,大家一定要理解,浮点数之间是没有绝对相等的。要比较他们是否相等,只要判断是不是在一个范围内即可,
if(fabs(f1 - f2) < 1e-6)
{
std::cout << "equal" << std::endl;
}
else
{
std::cout << "not equal" << std::endl;
}1.2 除法运算
用浮点做除法运算,本身是一件很危险的事情。因为f1/f2的时候,如果f2很小,那么f1/f2就会是非常大的一个数值。这样的话,这个结果本身其实是没有任何意义的。所以,即使要做除法运算,一定、一定要约束一下f2的数值范围。
1.3 数值滤波
SLAM中用到的数据大部分都是从传感器采集过来的。既然是采集的物理数据,就会不可避免地引入噪声。所以这个时候,就要对浮点数进行降噪处理,常用的方法一般有,
1)取平均值;
2)去掉最大值、最小值,取平均值;
3)v_new = v_old * 0.95 + v_capture * (1 - 0.95);
4)连续满足某个条件之后,才开始采样等等。
1.4 平方根
SLAM中的欧氏距离真的很好用。有的时候,最简单的方法往往就是最鲁棒的方法。所以distance = sqrt (pow(x, 2) + pow(y, 2))这样的计算方法一定要多看多用。
2、角度的计算
在一个平面上面,假设有一个x轴和一个y轴,那么任何的坐标p都会被拆解为(x0,y0)。其中它和x轴的角度称之为theta,那么就会有了下面一些列的计算,
2.1 点p到原点的距离
r = sqrt (pow(x, 2) + pow(y, 2))2.2 对应的角度theta该如何计算
theta = atan(y0 / x0)2.3 角度和弧度的对应关系
rad = (angle * 2 * pi) / 3602.4 sin、cos、tan
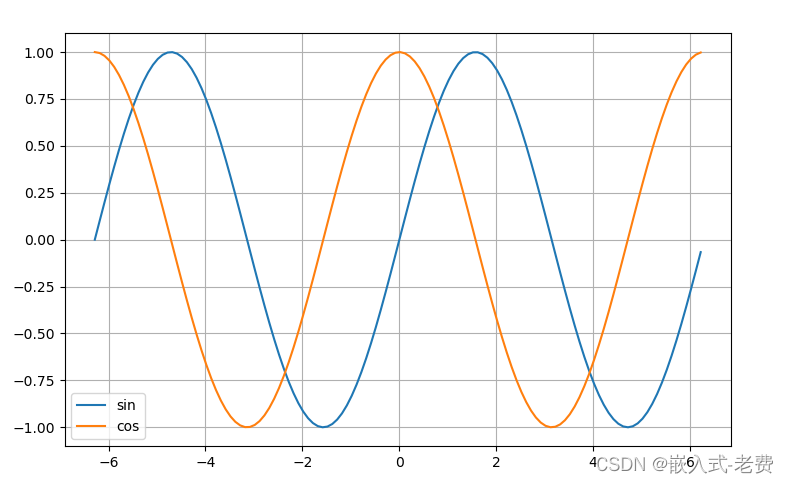
由于时间的关系,大家对于sin、cos、tan的周期性可能没有那么熟悉了,这里为了方便大家回忆。我们分别贴上sin&cos的周期图、tan的周期图。首先是sin&cos的周期图,
其次是tan的周期图,
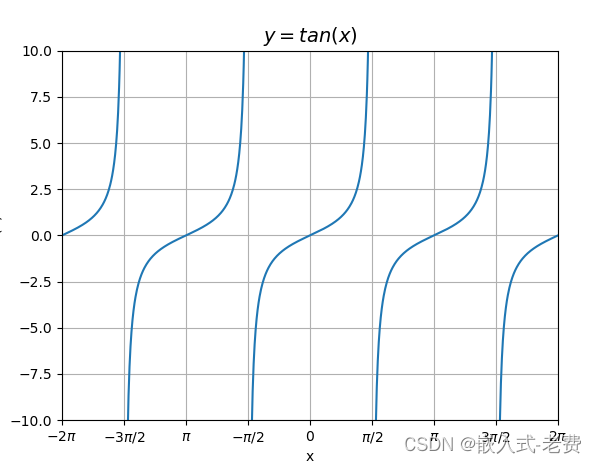
仔细观察下,sin的周期是2*pi,其中(-pi,0)为负,(0,pi)为正。cos的周期也是2*pi,其中(-pi/2,pi/2)为正,(-pi,-pi/2)&(pi/2,pi)为负。tan的周期是pi,其中(-pi/2,0)为负,(0,pi/2)为正。
2.5 一个有意思的旋转
之前我们谈到,假设有一个点,他处在(x0,y0),这个时候,如果逆时针旋转alpha角度,新的坐标是多少。要注意,这里面其实是有一个不变的量,那就是距离distance,也可以记着为r。按照道理,新的坐标应该是,
x1 = r * cos(theta + alpha)
y1 = r * sin(theta + alpha)如果仅仅是这样,那么数值并不太容易求出来,所以这里需要进一步分解一下,
x1 = r * cos(alpha + theta)
= r * (cos(alpha) * cos(theta) - sin(alpha) * sin(theta))
= x * cos(alpha) - y * sin(alpha)
y1 = r * sin(alpha + theta)
= r * (sin(alpha) * cos(theta) + cos(alpha) * sin(theta))
= x * sin(alpha) + y * cos(alpha)如果换成矩阵,其实写起来就很容易了,
[x1, y1] = [cos(alpha), -sin(alpha); sin(alpha), cos(alpha)] * [x, y]3、矩阵的计算
大学数学里面除了高等代数,也就是微分和积分之外,最重要的两门数学课就是线性代数和概率。而线性代数中最重要的计算就是矩阵。例2中提到的旋转,大家就可以转变成矩阵乘法的形式来进行处理,就是这样的,
pos_new = matrix * pos_old;有些同学也许忘记了矩阵的相关内容,没关系。其实大家只要会使用eigen这个库就好了。这个库是一个模板库,本身没有.a或者.so文件,直接使用即可。
sudo apt-get install libeigen3-dev4、概率的计算
概率这部分,大部分都是浮点的相关计算。中间以统计、加减法为主,本身困难不大。需要注意的地方就两个,一个是随机数的生成;一个就是高斯分布的生成。两个都很重要。
如果是随机数的生成,一般是先给一个种子,然后生成随机数,
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char *argv[])
{
int i;
srand((int) time(0));
for(i=0;i< 10;i++)
{
printf(" %d ", rand());
}
printf("n");
return 0;
}另外一个就是高斯分布的生成,两个参数,一个是平均值,一个是方差,
#include <random>
#include <chrono>
#include <iostream>
int main(int argc, char* argv[])
{
unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
std::default_random_engine generator(seed);
std::normal_distribution<double> distribution(0.0, 1.0);
for (int i = 0; i < 10; ++i)
{
std::cout << distribution(generator) << std::endl;
}
return 0;
}