一)知识回顾:

1)哈希表是什么?哈希表是存储数据的容器

2)哈希表有啥用?快速的查找某一个元素

3)什么时候使用哈希表?频繁的查找某一个数的时候，当我们快速查找某一个数的时候，不光要想到哈希表还需要想到二分查找，但是二分查找算法的局限性太强了，必须数组中有序或者是数组中出现二段性的时候才会使用到二分

4)如何让使用哈希表?

4.1)使用语言自带的容器

4.2)使用数组模拟简易哈希表hash<key，nums[index]，一般适用于字符串中的字符，可以使用数组下标来模拟字符的ASCILL码值，使用数组值可以是字符的个数，字符的下标，一般可以创建一个100-200个数组即可，这样就会使代码变得非常简洁，因为避免创建容器，使用容器中方法等等

4.3)但数据范围小的时候:1-10^2~3~4~4~5，但是当出现负数不建议使用数组

二)常见算法题:

一)两数之和:

1. 两数之和 - 力扣（LeetCode）

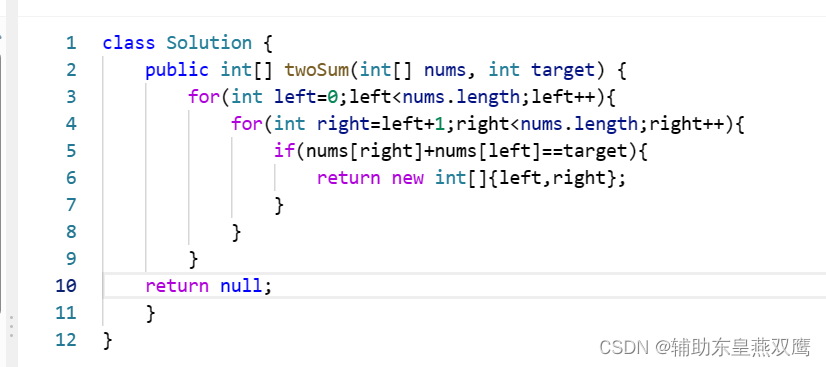
解法1:暴力枚举O(N^2)

1)我们首先每一次先固定一个数left，然后从这个数(不包含array[left])后面找到right下标的数使得array[left]+array[right]==target

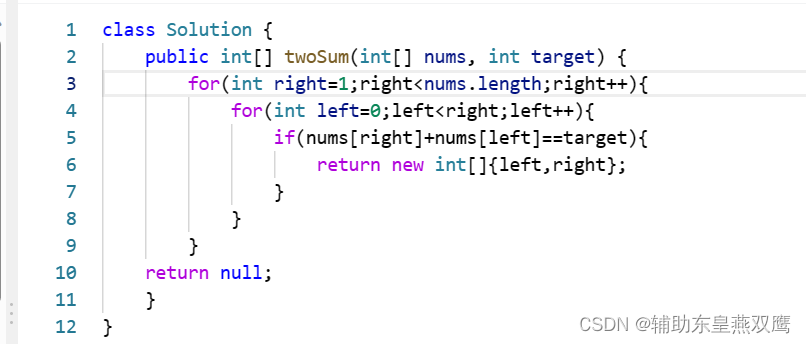
2)我们可以先固定最后一个数nums[right]，然后从这个数前面的数进行寻找nums[left]+nums[right]==target

暴力解法慢的原因就是每当我们固定一个数nums[index]之后，需要在这个数前面寻找target-nums[index]的数，此时还是需要使用遍历的方式进行查找，而如果我们要是使用哈希表的话，就可以快速找到要检索的元素

解法2:哈希表hash<nums[i]，下标>

当我们固定一个数right的时候，可以在哈希表中找到target-nums[right]的值，因为此时哈希表中存的都是nums[right]之前的数，这样就很好的规避了找到两个相同的数相加等于target，当没有找到的时候可以将nums[right]加入到哈希表中，right++，直到找到最终的结果即可

为什么之前的暴力策略不太好用呢？

之前使用的暴力策略是首先每一次先固定一个数left，然后从这个数(不包含array[left])后面找到right下标的数使得array[left]+array[right]==target，是需要将nums[left]后面的数(不包括nums[left])的数全部加入到哈希表中，如果是这样的话，是需要一开始将所有的数都加入到哈希表中，[2，4，5，8]，target=8，此时再来进行模拟就可能找到两个4相加等于8，可能自己找到自己了，所以还是需要特殊的进行判断的

class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer,Integer> result=new HashMap<>();
        for(int right=0;right<nums.length;right++){//先固定最后一个数
            if(result.containsKey(target-nums[right])){//再来枚举第一个数
                return new int[]{result.get(target-nums[right]),right};
            }else{
                result.put(nums[right],right);
            }
        }
        return null;
    }
}

二)判断是否互为字符重排:

面试题 01.02. 判定是否互为字符重排 - 力扣（LeetCode）

1)回溯:时间超时

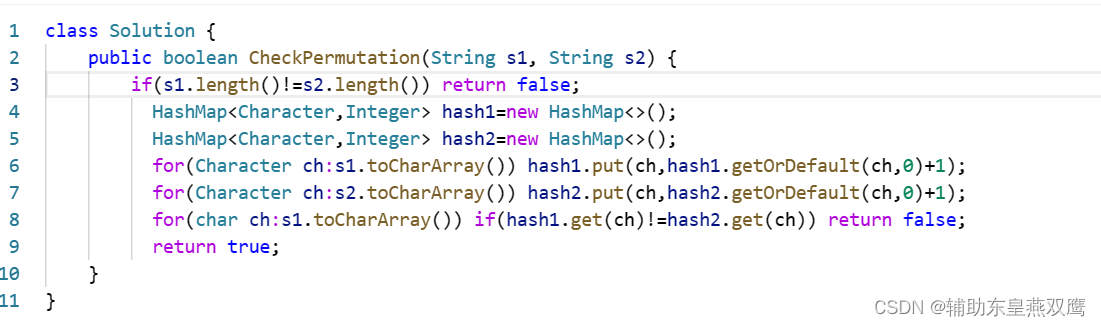
class Solution {
    List<String> result=new ArrayList<>();
    boolean[] check;
    StringBuilder path=new StringBuilder();
    public void dfs(char[] array){
        if(path.length()==array.length) {
             result.add(path.toString());
             return;
        }
        for(int i=0;i<array.length;i++){
            if(check[i]==false){
                path.append(array[i]);
                check[i]=true;
                dfs(array);
                check[i]=false;
                path.deleteCharAt(path.length()-1);
            }
        }
    }
    public boolean CheckPermutation(String s1, String s2) {
         char[] array=s1.toCharArray();
         this.check=new boolean[array.length];
         dfs(array);
         return result.contains(s2);
    }
}

 2)使用官方提供的哈希表

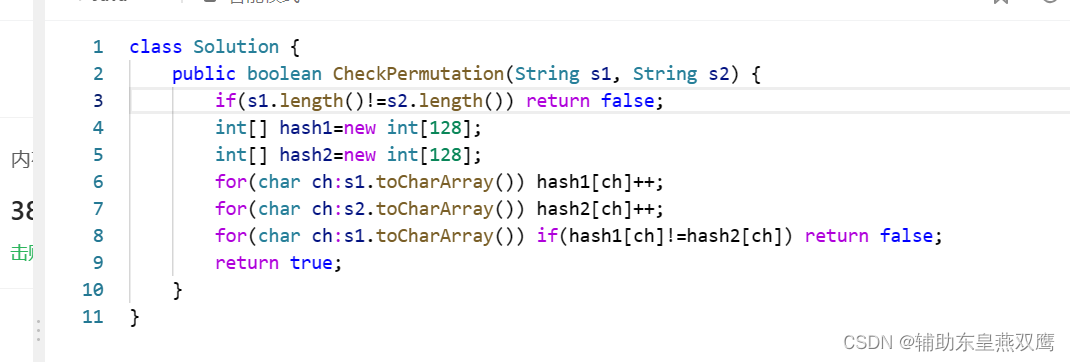
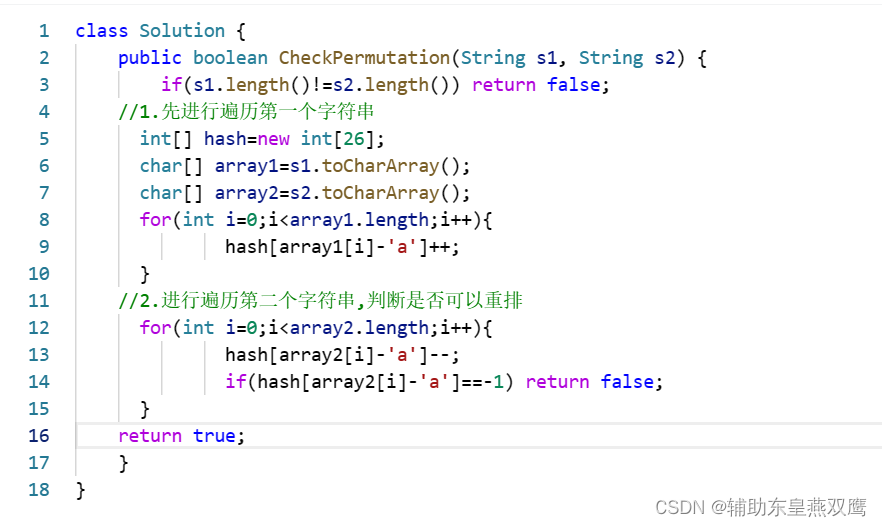
3)使用数组模拟的哈希表来解决这道问题

4)只使用一个哈希表来解决这道问题

三)存在重复元素

217. 存在重复元素 - 力扣（LeetCode）

哈希表:固定一个数right，看看right前面的数有没有出现过array[right]，如果出现过直接返回，如果没有出现过就把这个数加入到哈希表中，和之前做两数之和的逻辑是一样的，就是先固定末尾的数找找前面有没有出现过这个数即可

class Solution {
    public boolean containsDuplicate(int[] nums) {
        HashMap<Integer,Integer> result=new HashMap<>();
for(int right=0;right<nums.length;right++){//枚举后面的数,找找这个数在前面有没有出现过
            if(result.containsKey(nums[right])) return true;
            result.put(nums[right],right);
        }
    return false;//说明此时所有的元素都是不重复的
    }
}

四)存在重复元素(2)

219. 存在重复元素 II - 力扣（LeetCode）

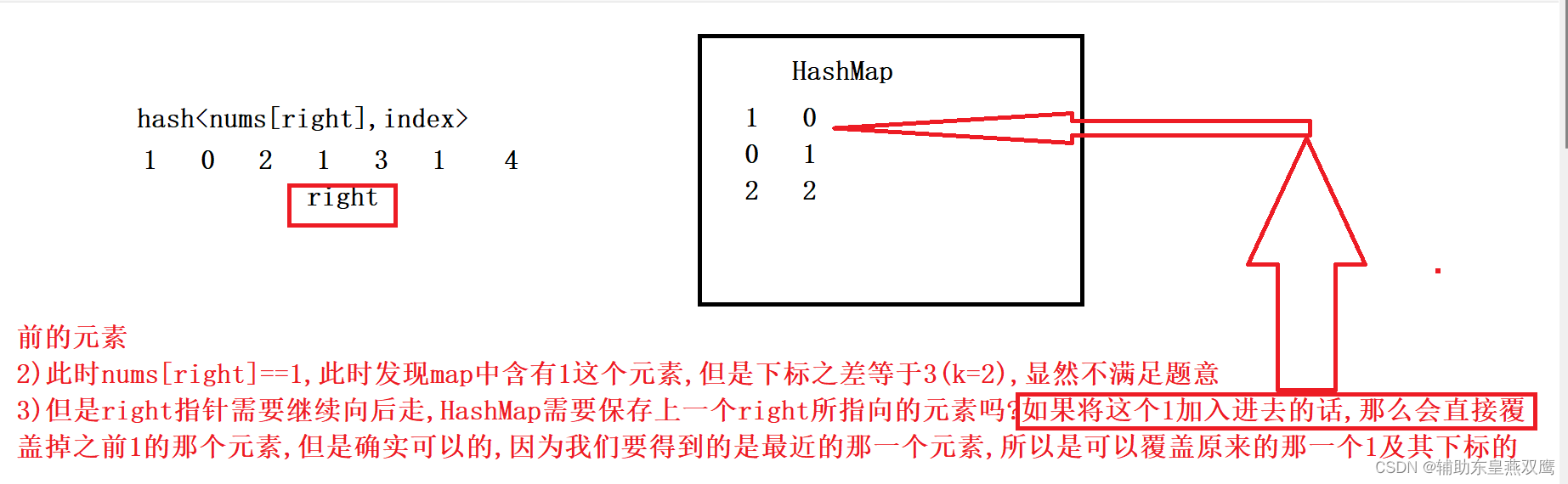
这道题相比于上道题来说来说有一个需要注意的点，就是找到最近的一个重复元素，前面的元素就不需要进行考虑的，所以出现重复元素的时候，我们是可以大胆地把之前的元素覆盖掉的，一定不会影响我们的最终结果的

class Solution {
    public boolean containsNearbyDuplicate(int[] nums, int k) {
        HashMap<Integer,Integer> result=new HashMap<>();
        for(int right=0;right<nums.length;right++){
            if(result.containsKey(nums[right])&&(Math.abs(right-result.get(nums[right]))<=k)){
                return true;
            }
            result.put(nums[right],right);//不用担心覆盖掉之前的元素
        }
     return false;
    }
}