1. 范数的定义

定义1-1：设 $E$ 为向量空间，$\mathbb{R}$ 为实数域。若映射
$$\begin{array}{c}\Vert \cdot \Vert :E\to \mathbb{R}:x\mapsto \Vert x\Vert \end{array}$$
对 $\forall x,y\in E;\lambda \in \mathbb{R}$ 满足

    ~~~     1) 正定性：$\Vert x\Vert ⩾0$ ，当且仅当 $x=0$ 时取等号;

    ~~~     2) 正齐次性：$\Vert \lambda x\Vert =|\lambda |\cdot \Vert x\Vert$;

    ~~~     3) 三角不等式：$\Vert x+y\Vert ⩽\Vert x\Vert +\Vert y\Vert$;

则将其称为范数，为区分定义在不同向量空间上的范数，也记作 $\Vert \cdot {\Vert }_E$，而将 $(E,\Vert \cdot \Vert )$ 称为赋范线性空间。

定理1-1：范数 $\Vert \cdot \Vert$ 是一个凸函数，即
$$\begin{array}{c}\Vert \lambda x+(1-\lambda )y\Vert ⩽\lambda \Vert x\Vert +(1-\lambda )\Vert y\Vert ,\forall x,y\in E;\lambda \in [0,1]\end{array}$$证明：由范数定义中的三角不等式：
$$\begin{array}{rl}\Vert \lambda x+(1-\lambda )y\Vert & ⩽\Vert \lambda x\Vert +\Vert (1-\lambda )y\Vert \\ & =|\lambda |\cdot \Vert x\Vert +|1-\lambda |\cdot \Vert y\Vert \\ & =\lambda \Vert x\Vert +(1-\lambda )\Vert y\Vert \text{（证毕）}\end{array}$$

定理1-2：定义在向量空间 $E$ 上的范数 $\Vert \cdot \Vert$ 满足不等式：
$$\begin{array}{c}|||x||-||y|||\le ||x\pm y||\le ||x||+||y||,x,y\in E\end{array}$$证明：由三角不等式：
$$\{\begin{array}{l}||x-y||+||y||\ge ||x||⟹||x-y||\ge ||x||-||y||\\ ||x-y||+||x||=||y-x||+||x||\ge ||y||⟹||x-y||\ge ||y||-||x||\end{array}$$故有：
$$\begin{array}{c}|||x||-||y|||\le ||x-y||\end{array}$$又
$$\begin{array}{c}||x-y||\le ||x||+||-y||=||x||+||y||\text{（证毕）}\end{array}$$

2. 常见的范数举例

例 $1$：定义在 实数空间 $\mathbb{R}$ 上的范数 ：
$$\Vert x\Vert =|x|,x\in \mathbb{R}$$容易验证上述定义是满足范数的三点要求的。

例 $2$：定义在 $n$ 维 Euclidean 空间 ${\mathbb{R}}^n$
$$\begin{array}{c}{\mathbb{R}}^n=\{x=(x_1,x_2,\cdots ,x_n)|x_i\in \mathbb{R},1=1,2,\cdots ,n\}\end{array}$$上的 $p$-范数：
$$\begin{array}{c}||x|{|}_p\triangleq {\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}},x\in {\mathbb{R}}^n;p\in [1,\infty )\end{array}$$
特比地，
$$\{\begin{array}{ll}\text{1-范数:}& ||x|{|}_1\triangleq \sum _{i=1}^n|x_i|\\ \text{2-范数（欧式范数）:}& ||x|{|}_2\triangleq \sqrt{\sum _{i=1}^n{x}_i^2}\\ \text{∞-范数（最大范数）:}& ||x|{|}_{\infty }\triangleq \underset{1\le i\le n}{\max }|x_i|\end{array}$$

证明：先验证上述“范数”的定义满足范数的三点要求 ：

1） 正定性 :
$$||x|{|}_p={\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}\ge 0$$上述不等式取等号时，当且仅当
$$|x_i|=0(i=1,2,\dots ,n)⟺x=0$$ 2）正齐次性 ：
$$||\lambda x|{|}_p={\left(\sum _{i=1}^n(|\lambda |\cdot |x_i|{)}^p\right)}^{\frac{1}{p}}=|\lambda |{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}=|\lambda |\cdot ||x|{|}_p$$3）三角不等式：
$$\begin{array}{rl}& \sum _{i=1}^n|x_i+y_i{|}^p\\ & \\ & =\sum _{i=1}^n|x_i+y_i{|}^{p-1}|x_i+y_i|\\ & \\ & \le \sum _{i=1}^n|x_i+y_i{|}^{p-1}(|x_i|+|y_i|)\\ & \\ & =\sum _{i=1}^n|x_i+y_i{|}^{p-1}|x_i|+\sum _{i=1}^n|x_i+y_i{|}^{p-1}|y_i|\\ & \\ & \le {\left[\sum _{i=1}^n|x_i+y_i{|}^{q(p-1)}\right]}^{\frac{1}{q}}{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}+{\left[\sum _{i=1}^n|x_i+y_i{|}^{q(p-1)}\right]}^{\frac{1}{q}}{\left(\sum _{i=1}^n|y_i{|}^p\right)}^{\frac{1}{p}}(pq=pq-q;p,q>1)\\ & \\ & =\left[{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}+{\left(\sum _{i=1}^n|y_i{|}^p\right)}^{\frac{1}{p}}\right]{\left[\sum _{i=1}^n|x_i+y_i{|}^{q(p-1)}\right]}^{\frac{1}{q}}\\ & \\ & =\left[{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}+{\left(\sum _{i=1}^n|y_i{|}^p\right)}^{\frac{1}{p}}\right]{\left[\sum _{i=1}^n|x_i+y_i{|}^p\right]}^{\frac{1}{q}}\end{array}$$上述证明过程前后应用了绝对值不等式与Holder不等式，进一步：
$${\left[\sum _{i=1}^n|x_i+y_i{|}^p\right]}^{1-\frac{1}{q}}={\left[\sum _{i=1}^n|x_i+y_i{|}^p\right]}^{\frac{1}{p}}\le \left[{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}+{\left(\sum _{i=1}^n|y_i{|}^p\right)}^{\frac{1}{p}}\right](p>1)$$当 $p=1$ 时由绝对不等式知上述不等式同样成立，综上得证Minkowski不等式（闵可夫斯基不等式）：
$${\left[\sum _{i=1}^n|x_i+y_i{|}^p\right]}^{\frac{1}{p}}\le \left[{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}+{\left(\sum _{i=1}^n|y_i{|}^p\right)}^{\frac{1}{p}}\right]（p\ge 1）$$即，
$$||x+y|{|}_p\le ||x|{|}_p+||y|{|}_p$$ 最后说明，当 $p\to \infty$ 时，$p-$范数满足最大范数的定义。采用夹逼定理求极限，由于
$$0\le \underset{1\le i\le n}{\max }|x_i{|}^p\le \sum _{i=1}^n|x_i{|}^p\le n\left(\underset{1\le i\le n}{\max }|x_i{|}^p\right)$$又
$$\{\begin{array}{l}\underset{p\to \infty }{\lim }{\left(\underset{1\le i\le n}{\max }|x_i{|}^p\right)}^{\frac{1}{p}}=\underset{1\le i\le n}{\max }|x_i|\\ \\ \underset{p\to \infty }{\lim }{\left[n\left(\underset{1\le i\le n}{\max }|x_i{|}^p\right)\right]}^{\frac{1}{p}}=\underset{1\le i\le n}{\max }|x_i|\underset{p\to \infty }{\lim }{n}^{\frac{1}{p}}=\underset{1\le i\le n}{\max }|x_i|\end{array}$$故
$$||x|{|}_{\infty }=\underset{p\to \infty }{\lim }{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}=\underset{1\le i\le n}{\max }|x_i|\text{（证毕）}$$

3. 范数的等价

定义3-1：设 $\mathcal{N}(E)$ 为所有定义在向量空间 $E$ 上的范数构成的集合，对于 $\Vert \cdot \Vert ,\Vert \cdot {\Vert }^{\times }\in \mathcal{N}(E)$，若
$$\begin{array}{c}\exists \alpha ,\beta \in {\mathbb{R}}^{+},s.t.\alpha \Vert x{\Vert }^{\times }⩽\Vert x\Vert ⩽\beta \Vert x{\Vert }^{\times },for\forall x\in E\end{array}$$则称 范数$\Vert \cdot \Vert$与$\Vert \cdot {\Vert }^{\times }$等价，记作： $\Vert \cdot \Vert \sim \Vert \cdot {\Vert }^{\times }$。

定理3-1 ：范数的等价具有传递性，即
$$\begin{array}{c}||\vec{x}|\sim ||\vec{x}|{|}^{\times },||\vec{x}||\sim ||\vec{x}|{|}^{\times \times }⟹||x|{|}^{\times }\sim ||x|{|}^{\times \times },\forall x\in E\end{array}$$

证明：若 $||\vec{x}||$ 与 $||\vec{x}|{|}^{\times }$ 等价，且 $||\vec{x}||$ 与 $||\vec{x}|{|}^{\times \times }$ 等价，则 $\exists c_i\in \mathbb{R},i=1,2,3,4$ 使得 ：
$$\{\begin{array}{l}{c}_1||x||\le ||x|{|}^{\times }\le c_2||x||\\ c_3||\vec{x}|{|}^{\times \times }\le ||x||\le c_4||\vec{x}{|}^{\times \times },\forall x\in E\end{array}$$那么，
$$c_1{c}_3||x|{|}^{\times \times }\le ||x|{|}^{\times }\le c_2{c}_4||\vec{x}|{|}^{\times \times },\forall x\in E$$故 $||x|{|}^{\times }$ 与 $||x|{|}^{\times \times }$等价。

定理3-2：定义在 ${\mathbb{R}}^n$ 上的 $1-$范数、$2-$范数、$\infty -$范数间满足：
$$\begin{array}{c}\Vert x{\Vert }_{\infty }⩽\Vert x{\Vert }_2⩽\Vert x{\Vert }_1⩽n\Vert x{\Vert }_{\infty },\forall x\in {\mathbb{R}}^n\end{array}$$故
$$\Vert x{\Vert }_1\sim \Vert x{\Vert }_2\sim \Vert x{\Vert }_{\infty }$$

证明：显然
$$\underset{1\le i\le n}{\max }|x_i|\le \sum _{i=1}^n|x_i|\le n\left(\underset{1\le i\le n}{\max }|x_i|\right)⟹\Vert x{\Vert }_{\infty }⩽\Vert x{\Vert }_1⩽n\Vert x{\Vert }_{\infty }$$又
$$\sqrt{x_1^2+x_2^2+\cdots +x_N^2}⩾\sqrt{{\left(\underset{1\le i\le n}{\max }|x_i|\right)}^2}=\underset{1\le i\le n}{\max }|x_i|⟹\Vert x{\Vert }_{\infty }⩽\Vert x{\Vert }_2$$且根据 Cauchy-Bunjakovski 不等式（Cauchy–Schwarz 不等式）可得
$$x_1^2+x_2^2+\cdots +x_N^2\le (|x_1|+|x_2|+\cdots +|x_N|{)}^2⟹||x|{|}_2⩽||x|{|}_1\text{（证毕）}$$

4. 距离与度量空间的定义

定义4-1：设 $S$ 是非空集合（不一定是向量空间），若映射
$$\begin{array}{c}d:S\times S\to \mathbb{R}:(x,y)\mapsto d(x,y)\end{array}$$满足：

    ~~~     1) 正定性：$d(x,y)⩾0$ ，当且仅当 $x=y$ 时取等号;

    ~~~     2) 对称性：$d(x,y)=d(y,x)$;

    ~~~     3) 三点不等式：$d(x,y)⩽d(x,z)+d(z,y)$.

则称 $d(x,y)$ 为 $x$ 到 $y$ 的距离，并将 $(S,d)$ 称为度量空间。

定理4-1：对于赋范向量空间 $(E,\Vert \cdot \Vert )$，若取
$$\begin{array}{c}d(x,y)\triangleq \Vert x-y\Vert ,\forall x,y\in E\end{array}$$则在向量空间 $E$ 上定义了距离 $d(x,y)$，即赋范线性空间可视为度量空间，并将上式定义的 $d(x,y)$ 称为由范数 $\Vert \cdot \Vert$ 导出的距离。由范数 $\Vert \cdot \Vert$ 导出的距离 $d(x,y)$ 满足：
$$\{\begin{array}{l}d(x-y,0)=||(x-y)-0||=||x-y||=d(x,y)\\ d(\lambda x,0)=||\lambda x-0||=||\lambda x||=|\lambda |\cdot ||x-0||=|\lambda |d(x,0)(\forall x,y\in E;\lambda \in \mathbb{R})\end{array}$$

证明：验证给出的距离取法是否满足距离的定义 ，对 $\forall x,y,z\in E$

1）正定性：$$\begin{array}{c}d(x,y)=||x-y||\ge 0,\text{（当且仅当 x−y=0⟹x=y 时取等号）}\end{array}$$2）对称性：$$\begin{array}{c}d(x,y)=||x-y||=||-(y-x)||=||y-x||=d(y,x)\end{array}$$3）三点不等式：$$\begin{array}{c}d(x,z)+d(z,y)=||x-z||+||z-y||\ge ||(x-z)+(z-y)||=||x-y||=d(x,y)\text{（证毕）}\end{array}$$
定理4-2：设 $(S,d)$ 为定义了距离的线性空间，若距离 $d$ 满足：
$$\{\begin{array}{l}d(x-y,0)=d(x,y)\\ d(\lambda x,0)=|\lambda |d(x,0)(\forall x,y\in S;\lambda \in \mathbb{R})\end{array}$$则可以取
$$\begin{array}{c}||x||\triangleq d(x,0),x\in S\end{array}$$使得定义出的 $\Vert \cdot \Vert$ 为范数，并且使得 $d$ 是由 $\Vert \cdot \Vert$ 导出的距离。

证明：验证给出的范数取法是否满足范数的定义 ，对 $\forall x,y\in S,\lambda \in \mathbb{R}$

1）正定性：$$\begin{array}{c}||x||=d(x,0)\ge 0,\text{（当且仅当 x=0 时取等号）}\end{array}$$2）正齐次性：$$\begin{array}{c}||\lambda x||=d(\lambda x,0)=|\lambda |d(x,0)=|\lambda |\cdot ||x||\end{array}$$3）三角不等式：$$\begin{array}{rl}||x||+||y||& =d(x,0)+d(y,0)=d(x,0)+d(-y,0)\\ & =d(x,0)+d(0,-y)\ge d(x,-y)=d(x+y,0)=||x+y||\end{array}$$故所取的范数形式满足范数的定义，即 $S$ 可视为赋范线性空间。最后说明 $d$ 是由 $\Vert \cdot \Vert$ 导出的距离：
$$\forall x,y\in S,d(x,y)=||x-y||=d(x-y,0)$$

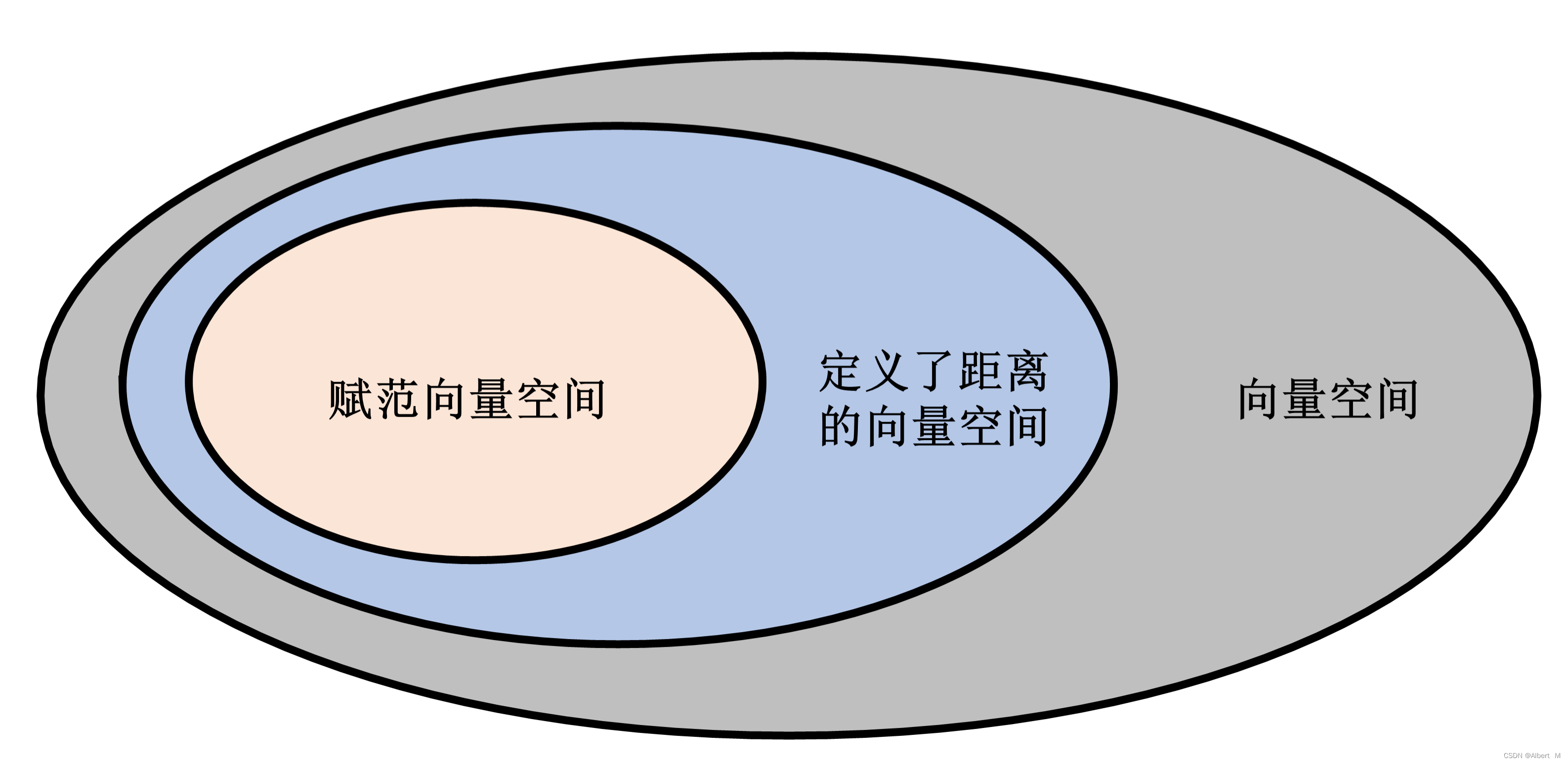
结合上述两条定理，可得如下包含关系：