139.单词拆分

题目链接 | 理论基础

乍一看是回溯问题，和分割回文子串很像，不过本题使用回溯解决会超时（有些极端 case 过不了），而且这样只需要求解 True/False 的问题一般不会考虑回溯，毕竟回溯是暴力的指数搜索。

将 wordDict 看作可以无限取用的物品，s 看作是背包，问能否用物品填满背包 – 完全背包，启动！
注意到本题的结果是必须依赖于排列的，只靠组合不能确定结果，因为填满背包的方式是有顺序要求的，同样是 wordDict = ["apple", "pen"]，["apple", "pen", "apple"] 就可以得到 "applepenapple"，而 ["apple", "apple", "pen"] 不可以。用爬楼梯的思路来解决的话会流畅一些。

dp 数组的下标含义：dp[j] 代表是否能够填满背包 s[:j]
dp 递推公式：dp[j] = dp[j] or dp[j - len(wordDict[i])]
- 不需要当前的单词 wordDict[i]，就已经能组合成 s[:j]
- 需要当前的单词 wordDict[i]，并且之前已经能组成 s[:j-len(wordDict[i])]
  - “需要当前单词”代表着 s[j - len(wordDict[i]): j] == wordDict[i] 成立
- 以上情况只要有一种成立，就能够得到 dp[j]=True
dp 数组的初始化：根据递推公式可以得到 dp[0]=True，否则后面的递推无法进行
- 从逻辑上来说，dp[0] 的取值没有明确定义，但是 dp[0]=True 能够使得 wordDict = ["pen"], s = "pen" 的情况推导出正确的 dp 数组
dp 的遍历顺序：如上所述，这道题的结果依赖于排列而非组合，很明显必须是先背包再物品（爬楼梯 yyds）
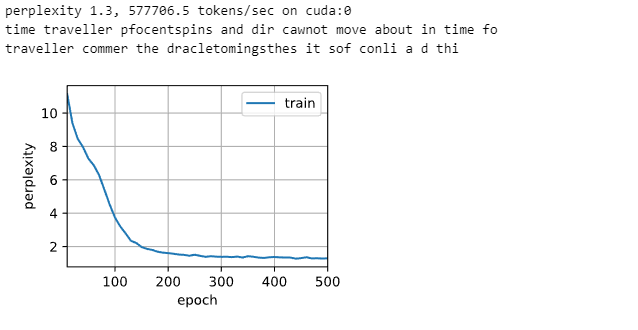
举例推导：wordDict = ["leet", "code"], s = "leetcode"

0 1 2 3 4 5 6 7 8
dp T F F F T F F F T

	0	1	2	3	4	5	6	7	8
dp	T	F	F	F	T	F	F	F	T

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        # dp[j] represents whether can make s[:j] 
        dp = [False] * (len(s) + 1)
        dp[0] = True

        # dp formula, bag->item
        for j in range(1, len(s) + 1):
            for i in range(len(wordDict)):
                if j >= len(wordDict[i]) and s[j - len(wordDict[i]): j] == wordDict[i]:
                    dp[j] = dp[j] or dp[j - len(wordDict[i])]
        
        return dp[-1]

多重背包

理论基础

给定一个限重为 $V$ 的背包，有 $N$ 种物品，其中第 $i$ 件物品有 $M_i$ 个可用，每一件消耗空间 $C_i$ ，价值是 $W_i$ 。求怎样装入物品，使得物品总重量不会超过背包限重，同时获得最大价值。

最简单的等价转换就是将多重背包转化为 01 背包问题。将每种物品每一件都摊开来，就是 01 背包，毕竟 01 背包也没有规定物品的重量、价值不能相同。
如下，第一张表是完全背包，第二张表是 01 背包：

	物品价值	物品重量	数量
物品 0	1	15	1
物品 1	3	20	3
物品 2	4	30	2

	物品价值	物品重量
物品 0	1	15
物品 1	3	20
物品 1	3	20
物品 1	3	20
物品 2	4	30
物品 2	4	30

所以，只要将多重背包正确地转换成 01 背包的输入，就可以用 01 背包的方法来解决。转换代码如下：

weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bagWeight = 10

# 将数量大于1的物品展开
for i in range(len(nums)):
    while nums[i] > 1:
        weight.append(weight[i])
        value.append(value[i])
        nums[i] -= 1

另一种思路就是在物品+背包的遍历内部再加上一层使用数量的遍历。之前的 01 背包，无论是二维数组还是滚动数组，无论遍历顺序，都需要考虑“当前背包容量为 j，是否要取物品 i”；现在的滚动背包内，需要考虑“当前背包容量为 j，要取多少件物品 i”。
本质上还是很像爬楼梯。

def test_multi_pack(weight, value, nums, bagWeight):
    dp = [0] * (bagWeight + 1)

    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            # 以上为01背包，然后加一个遍历个数
            for k in range(1, nums[i] + 1):  # 遍历个数
                if j - k * weight[i] >= 0:
                    dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i])

        # 使用 join 函数打印 dp 数组
        print(' '.join(str(dp[j]) for j in range(bagWeight + 1)))

    print(dp[bagWeight])


if __name__ == "__main__":
    weight = [1, 3, 4]
    value = [15, 20, 30]
    nums = [2, 3, 2]
    bagWeight = 10
    test_multi_pack(weight, value, nums, bagWeight)

背包问题总结

理论基础

在这里插入图片描述
通过之前这一堆背包问题的练习，解决背包问题已经比较有套路了，对遍历顺序、初始化的理解也算不错。然而，将复杂的问题背景抽象成背包问题，仍然是需要经过思考的，其中最后一块石头的重量 II、目标和绝对是这种复杂抽象的难题。
另外，很多背包问题看上去也都能用回溯算法解决，但毫无疑问都一定会超时。区别在于，背包问题依然能够依靠子问题的解来节省复杂度，而回溯算法不可避免地需要进行穷举，只不过是优雅的穷举，两者还是有本质上的区别。

代码随想录上总结了不同的递推公式。但这些背包问题刷下来，个人感觉找对了 dp 数组的含义后，dp 递推公式就能很自然地得到，无需特别考虑。相比之下，初始化和遍历顺序才是更大的坑。

初始化

背包问题的初始化堪称是五花八门，每一道题都需要谨慎思考。找到正确的初始化，最好的方法是对于自己的想法，找个简单的例子推一下，看看能否得到想要的答案。

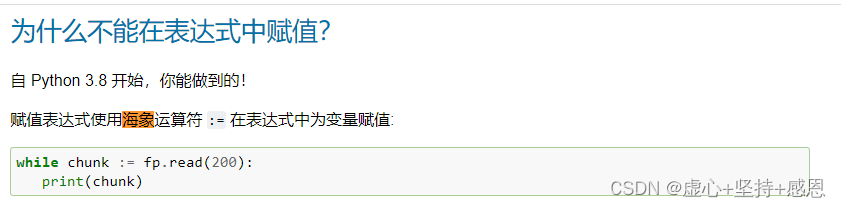
有些简单的 dp 题，dp 数组的部分初始化根本不重要，例如爬楼梯中的 dp[0]。这种情况下，最重要的是确保自己的初始化能够正确地得到后续的结果即可。
二维数组解背包问题，最重要的是对于 i=0 的初始化，因为后续操作 dp[i][j] 的时候要用到 dp[i-1][...] 的值。二维数组的初始化一般比较直观，能够根据含义直接得到 i=0 和 j=0 时的值，通常来说也能帮助顺利得到正确的递推结果。
- 目标和堪称是二维数组初始化的难度巅峰。
滚动数组解背包问题，相对来说初始化更容易一些，因为这个一维数组中一般只需要初始化 dp[0]，要思考的东西大大减少了。相对应的，滚动数组的初始化更为抽象，因为这里的初始化是没有发生更新之前，需要结合递推公式来得到合理的初始化值。
对于不特殊的 dp 数组位置，初始化同样要小心。无脑初始化为 0 或 -1 绝对不是明智的选择。
- 零钱兑换就是初始化大坑的巅峰。

遍历顺序

01 背包
- 二维数组：先物品后背包、先背包后物品都是可以的，内部循环从小到大、从大到小进行都可以
- 滚动数组：对于背包的遍历必须是从大到小反向遍历（否则可能重复选取同一物品），从而导致必须是先物品后背包（否则每个背包容量都只能选取一件物品）
完全背包
- 二维数组仍然不在乎遍历顺序
  - 限制于二维数组总是根据之前的状态进行递推，二维数组似乎并不能解决
- 滚动数组：纯粹的完全背包只在乎最终容量能够得到的价值，不在乎得到的方式（顺序），所以先物品后背包、先背包后物品都是可以的，背包的遍历必须是从小到大（才能捕捉到重复使用）
  - 如果完全背包问题要求组合结果，那就必须是先物品后背包（相当于固定了物品的出现顺序）
  - 如果完全背包问题要求排列结果，那就必须是先背包后物品（相当于允许了任意的物品顺序）
    - dp 解决排列问题，最好的抽象方法是爬楼梯！
  - 如果完全背包问题不在意结果的顺序，那么物品、背包的先后顺序就无所谓了