x.1 矩阵空间

向量空间定义：满足加法和数乘的封闭性。就类似向量空间一样，也存在着矩阵空间的定义。举个例子，例如所有的3x3的矩阵构成的矩阵空间M，它的纬度就是9，如[1, 0, …], [0, 1, …]。对于M中所有对称矩阵组成子空间N1，维度为6。M中所有上三角矩阵组成子空间N2，维度为6。M中所有对角矩阵组成子空间N3，维度为3。

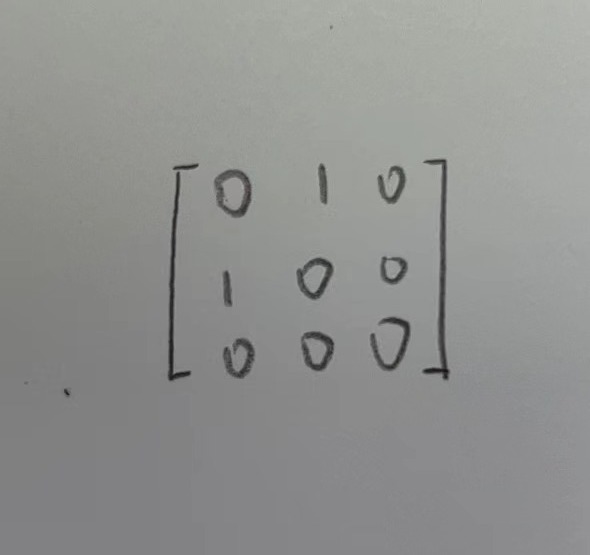
我们对于矩阵子空间，往往更在乎的是交∩，加+运算，而并不在意并∪运算，因为∩，+更有意义。例如对称矩阵N1和上三角矩阵N2的∩构成了对角矩阵N3，而对称矩阵N1和上三角矩阵N2的+构成了全部的空间M。所以我们得到一个朴素的道理，对于两个矩阵子空间，他俩维度相加存在如下定理，

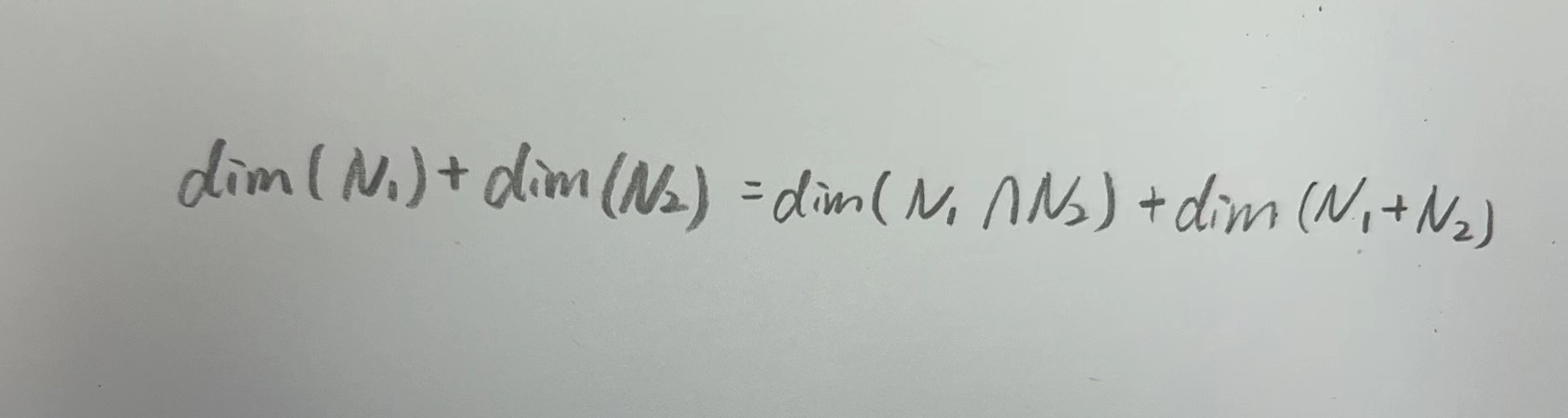
与微分方程联系，举一个2阶判断维度的例子，

x.2 秩为1的矩阵

任何秩为1的矩阵都可以看做一列乘以一行，而秩不为1的矩阵可以通过若干秩为1的矩阵相加，再将秩为1的矩阵看做一列乘以一行。我们需要具备上面的分解的思想，如同搭积木一样。

注意，我们需要将对秩为1的矩阵A的分解思想和对矩阵A, B相乘等于线性组合的思想分离开，

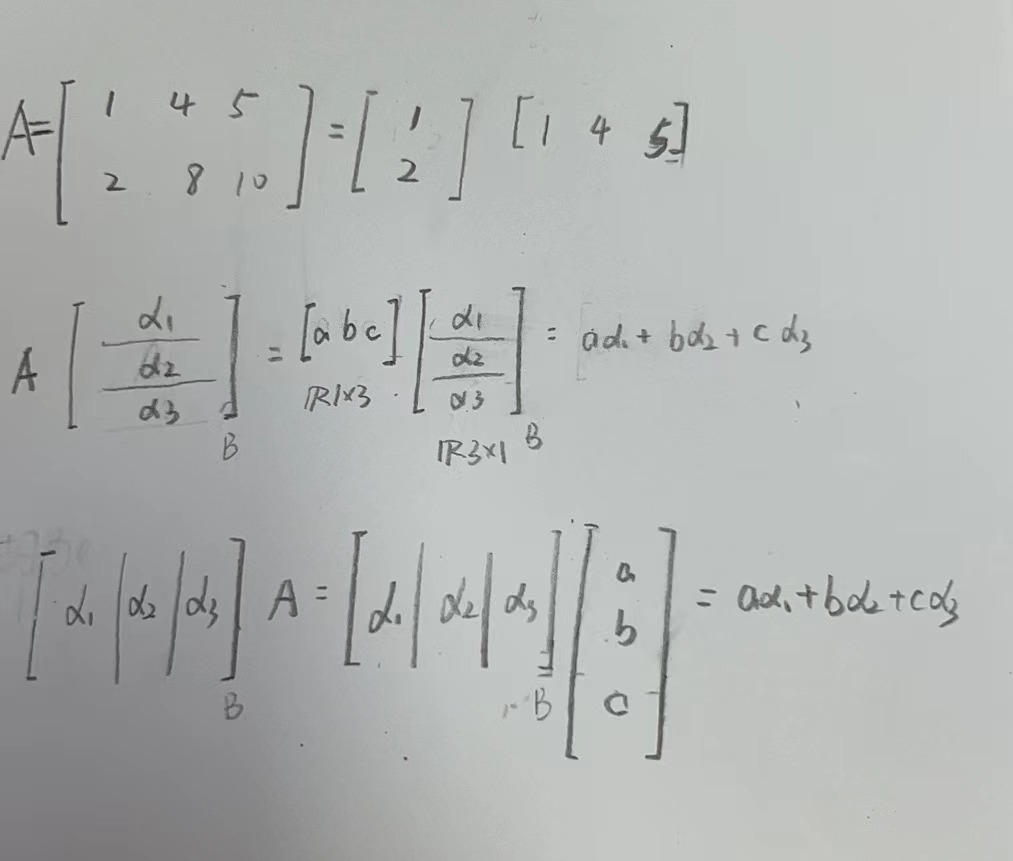
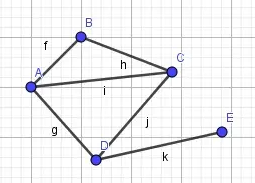
x.3 小世界图

即将图论思想引入，例如如果人代表一个节点，而人和人的关系是线，则世界有多小，实际上最多通过6条边你便可以联系上世界上所有的人，图={节点，边}。