数据结构与算法基础-学习-30-插入排序之直接插入排序、二分插入排序、希尔排序

news2024/10/5 16:57:14

一、排序概念

将一组杂乱无章的数据按一定规律顺次排列起来。

将无序序列排成一个有序序列（由小到大或由大到小）的运算。

二、排序方法分类

1、按数据存储介质

名称描述
内部排序数据量不大、数据在内存，无需内外交换存交换存储。
外部排序数据量较大、数据在外存（文件排序）外部排序时，要将数据分批调入内存来排序，中间结果还是要及时放入外存，显然外部排序要复杂得多。

2、按比较器个数

名称描述
串行排序单处理机。（同一时刻比较一对元素）
并行排序多处理机。（同一时刻比较多对元素）

3、按主要操作

名称描述
比较排序用比较的方法（插入排序、交换排序、选择排序、归并排序）
基数排序不比较元素的大小，仅仅根据元素本身的取值确定其有序位置。

4、按辅助空间

名称描述
原地排序辅助空间用量为O(1)的排序方法。（所占的辅助存储空间与参加排序的数据量大小无关）
非原地排序辅助空间用量超过O(1)的排序方法。

5、按稳定性

名称描述
稳定排序能够使任何数值相等的元素，排序以后相对次序不变。
非稳定排序不是稳定排序的方法。

6、按自然性

名称描述
自然排序输入数据越有序，排序的速度越快的排序方法。
非自然排序不是自然排序的方法。

三、排序稳定性的意义

排序的稳定性只对结构类型数据排序有意义。

例如说我们只对分数进行排序，相同分数排序后是否更换位置，对于结果是没有影响的。然而我们对于数学分数、语文分数和人名进行综合排序，虽然数学分数相同的两个同学，但语文成绩不同，名次先后也会有某种变化。

排序方法是否稳定，并不能衡量一个排序算法的优劣。

四、插入排序基本思想

每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。

即便插入边排序，保证子序列中随时都是排好序的。

五、直接插入排序（哨兵）

1、算法思路

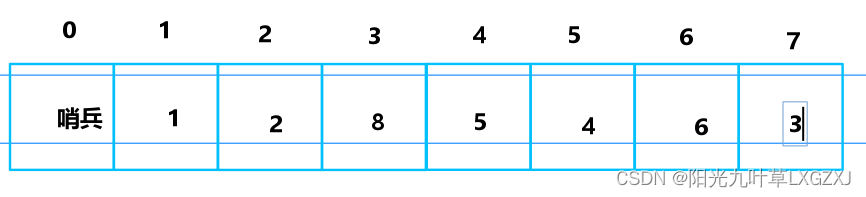
Data           : [ 0 ,1 ,2 ,8 ,5 ,4 ,6 ,3 ]

升序为例，1，2，8是排好序的，发现5比8小，将5放到哨兵位，8往后移动一位，哨兵再和2比，比2大，退出此次循环，原有8的位置换成哨兵5。

Data           : [ 5 ,1 ,2 ,5 ,8 ,4 ,6 ,3 ]

现在移动到下一位4，1，2，5，8是排好序的，发现4比8小，将4放到哨兵位，8往后移动一位，哨兵4再和5比发现小，5往后移动一位，哨兵再和2比，比2大，退出此次循环，原有5的位置换成哨兵4。

Data           : [ 4 ,1 ,2 ,4 ,5 ,8 ,6 ,3 ]

现在移动到下一位6，1，2，4，5，8是排好序的，发现6比8小，将6放到哨兵位，8往后移动一位，哨兵再和5比，比5大，退出此次循环，原有8的位置换成哨兵6。

Data           : [ 6 ,1 ,2 ,4 ,5 ,6 ,8 ,3 ]

现在移动到下一位6，1，2，4，5，6，8是排好序的，发现3比8小，将3放到哨兵位，且比4，5，6，8都小，4，5，6，8往后挪动一位，比2大，退出此次循环，原有4的位置换成哨兵3。

Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]

2、源码

（1）DirectInsertSortSentrySqQueue

Status DirectInsertSortSentrySqQueue(SqQueue* Queue)
{
    JudgeAllNullPointer(Queue);

    if (Queue->Flag != INT_TYPE_FLAG)
    {
        return FailFlag;
    }

    int*         Array = (int*)(Queue->Data);
    QueueLenType i;
    QueueLenType j;

    for (i = 2; i < Queue->SqQueueLen; i++)
    {
        if (Array[i] < Array[i - 1])//升序或降序
        {
            Array[0] = Array[i];
            for (j = i - 1; Array[0] < Array[j]; j--)
            {
                Array[j + 1] = Array[j];//移动元素
            }
            Array[j + 1] = Array[0];//插入到元素的后一位。
            PrintfSqQueue(Queue);
        }
    }
    
    LogFormat(Debug,"Direct Insert Sort Sentry SqQueue OK.\n");

    return SuccessFlag;
}

3、Linux环境编译测试

[gbase@czg2 Sort]$ make
gcc -Wall -Wextra -O3 InsertSort.c main.c -o TestSort -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/Log/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/HashTable/include/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqQueue/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqStack/ -L /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/Make/Libs/ -lPublicFunction -lLog -lSqQueue

[gbase@czg2 Sort]$ time ./TestSort 
2023-8-29--[ Debug ]--Init SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,1 ,2 ,8 ,5 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 5 ,1 ,2 ,5 ,8 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 4 ,1 ,2 ,4 ,5 ,8 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 6 ,1 ,2 ,4 ,5 ,6 ,8 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Direct Insert Sort Sentry SqQueue OK.
2023-8-29--[ Info  ]--Sort Function Elapsed Time   : 0 s
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Destroy SqQueue OK

real    0m0.002s
user    0m0.001s
sys     0m0.001s

六、二分插入排序（哨兵）

1、算法思路

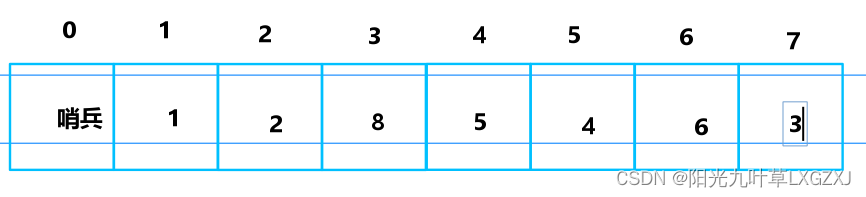
升序为例，1，2，8为有序序列，5小于8，5放到哨兵位， 开始进行二分查找，以Low <= High为进行条件。

2023-8-29--[ Debug ]--Low : 1, High : 3, Mid : 2.

Mid：2对应2，2小于5，Low = Mid + 1 = 3，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 3, High : 3, Mid : 3.

Mid：3对应8，5小于8，High = Mid - 1 = 2，不满足Low <= High，退出循环。

将8往后挪动一位。哨兵填写到原有8的位置，变化如下：

Data           : [ 5 ,1 ,2 ,5 ,8 ,4 ,6 ,3 ]

1，2，5，8为有序序列，4小于8，4放到哨兵位， 开始进行二分查找，以Low <= High为进行条件。

2023-8-29--[ Debug ]--Low : 1, High : 4, Mid : 2.

Mid：2对应2，2小于4，Low = Mid + 1 = 3，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 3, High : 4, Mid : 3.

Mid：3对应5，4小于5，High = Mid - 1 = 2，不满足Low <= High，退出循环。

将5，8往后挪动一位。哨兵填写到原有5的位置，变化如下：

Data           : [ 4 ,1 ,2 ,4 ,5 ,8 ,6 ,3 ]

1，2，4，5，8为有序序列，6小于8，6放到哨兵位， 开始进行二分查找，以Low <= High为进行条件。

2023-8-29--[ Debug ]--Low : 1, High : 5, Mid : 3.

Mid：3对应4，4小于6，Low = Mid + 1 = 4，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 4, High : 5, Mid : 4.

Mid：4对应5，5小于6，Low = Mid + 1 = 5，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 5, High : 5, Mid : 5.

Mid：5对应5，6小于8，High = Mid - 1 = 4，不满足Low <= High，退出循环。

将8往后挪动一位。哨兵填写到原有8的位置，变化如下：

Data           : [ 6 ,1 ,2 ,4 ,5 ,6 ,8 ,3 ]

1，2，4，5，6，8为有序序列，3小于8，3放到哨兵位， 开始进行二分查找，以Low <= High为进行条件。

2023-8-29--[ Debug ]--Low : 1, High : 6, Mid : 3.

Mid：3对应4，3小于4，High = Mid - 1 = 2，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 1, High : 2, Mid : 1.

Mid：1对应1，1小于3，Low = Mid + 1 = 2，Low <= High，继续循环。

2023-8-29--[ Debug ]--Low : 2, High : 2, Mid : 2.

Mid：2对应2，2小于3，Low = Mid + 1 = 3，不满足Low <= High，退出循环。

将4，5，6，8往后挪动一位。哨兵填写到原有4的位置，变化如下：

Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]

 2、源码

（1）BinaryInsertSortSentrySqQueue

Status BinaryInsertSortSentrySqQueue(SqQueue* Queue)
{
    JudgeAllNullPointer(Queue);

    if (Queue->Flag != INT_TYPE_FLAG)
    {
        return FailFlag;
    }

    int*         Array = (int*)(Queue->Data);
    QueueLenType i;
    QueueLenType j;
    QueueLenType Mid;
    QueueLenType High;
    QueueLenType Low;

    for (i = 2; i < Queue->SqQueueLen; i++)
    {
        if (Array[i - 1] < Array[i])//如果已经是有序的就不用进行二分查找
        {
            continue;
        }
        
        Array[0] = Array[i];//存放哨兵
        Low      = 1;
        High     = i - 1;
        while (Low <= High)//折半查找
        {
            Mid = (Low + High) / 2;
            LogFormat(Debug,"Low : %lld, High : %lld, Mid : %lld.\n",Low,High,Mid);
            if (Array[0] < Array[Mid])
            {
                High = Mid - 1;
            }
            else
            {
                Low = Mid + 1;
            }
        }
        for (j = i - 1; j >= High + 1; j--)//为什么High + 1，下次看见需推导几次，方便加深记忆。
        {
            Array[j + 1] = Array[j];//移动元素
            PrintfSqQueue(Queue,Debug);
        }
        Array[High + 1] = Array[0];//插入元素
    }
    
    LogFormat(Debug,"Binary Insert Sort Sentry SqQueue OK.\n");

    return SuccessFlag;
}

3、Linux环境编译测试

[gbase@czg2 Sort]$ time ./TestSort 
2023-8-29--[ Debug ]--Init SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,1 ,2 ,8 ,5 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Low : 1, High : 3, Mid : 2.
2023-8-29--[ Debug ]--Low : 3, High : 3, Mid : 3.
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 5 ,1 ,2 ,8 ,8 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Low : 1, High : 4, Mid : 2.
2023-8-29--[ Debug ]--Low : 3, High : 4, Mid : 3.
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 4 ,1 ,2 ,5 ,8 ,8 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 4 ,1 ,2 ,5 ,5 ,8 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Low : 1, High : 5, Mid : 3.
2023-8-29--[ Debug ]--Low : 4, High : 5, Mid : 4.
2023-8-29--[ Debug ]--Low : 5, High : 5, Mid : 5.
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 6 ,1 ,2 ,4 ,5 ,8 ,8 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Low : 1, High : 6, Mid : 3.
2023-8-29--[ Debug ]--Low : 1, High : 2, Mid : 1.
2023-8-29--[ Debug ]--Low : 2, High : 2, Mid : 2.
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,4 ,5 ,6 ,8 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,4 ,5 ,6 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,4 ,5 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,4 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Binary Insert Sort Sentry SqQueue OK.
2023-8-29--[ Info  ]--Sort Function Elapsed Time   : 0 s
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Destroy SqQueue OK

real    0m0.003s
user    0m0.001s
sys     0m0.002s

七、希尔排序（哨兵）

1、基本思想

先将整个待排记录序列分割成若干个子序列，分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

2、特点

（1）一次移动，移动位置较大，跳跃式地接近排序后的最终位置。

（2）最后一次只需要少量移动。

（3）增量序列必须是递减的，最后一个必须是1。

（4）增量序列应该是互质的。

3、算法效率与增量序列

（1）Hibbard

Dk = 2^k - 1 （相邻元素互质）

猜想情况算法时间复杂度
最坏O(n^(2 / 3))
平均O(n^(5 / 4))

（3）Sedgewick

Dk = 9 * 4^i - 9 * 2^i + 1 或者 4^i - 3 * 2^i + 1

猜想情况算法时间复杂度
最坏O(n^(4 / 3))
平均O(n^(7 / 6))

4、算法思路

这个算法涉及步长，因为插入排序算法，需要两个大步，一个是查找插入位置，二是移动元素。希尔排序在直接插入排序的基础上优化第二大步移动元素，不像之前是一步步移动，而是几步、几十步、几百步的移动。

假设步长分别为3和1，实际算法中肯定不是这么设置的步长，只是举例，方便之后举一反三。

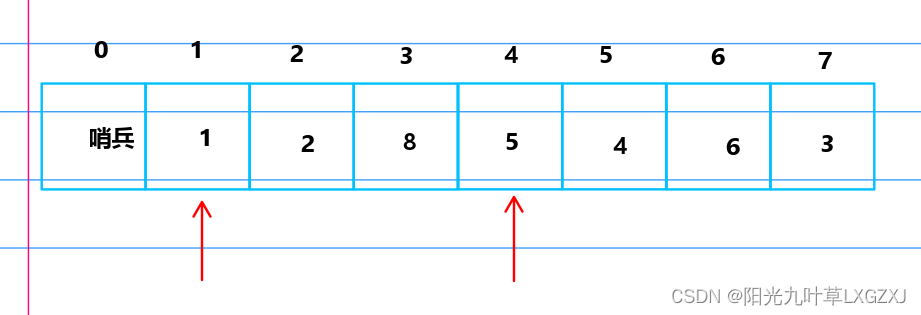
 比较1和5，发现1小于5，不需要进行排序，1号位的1前推3格超过1号位，不需要回推，前进一格。

 比较2和4，发现2小于4，不需要进行排序，2号位的2前推3格超过1号位，不需要回推，前进一格。

 比较8和6，发现8大于6，进行排序，6放到哨兵位，将8挪动到6的位置，再将哨兵的6放到原来8的位置，3号位的6前推3格超过1号位，不需要回推，前进一格。

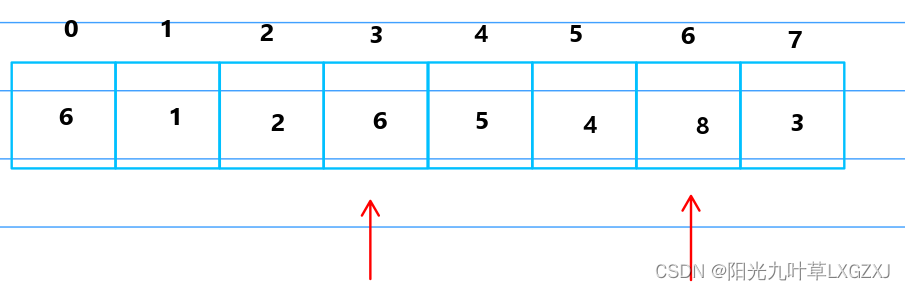 继续往后移动， 比较5和3，发现5大于3，进行排序。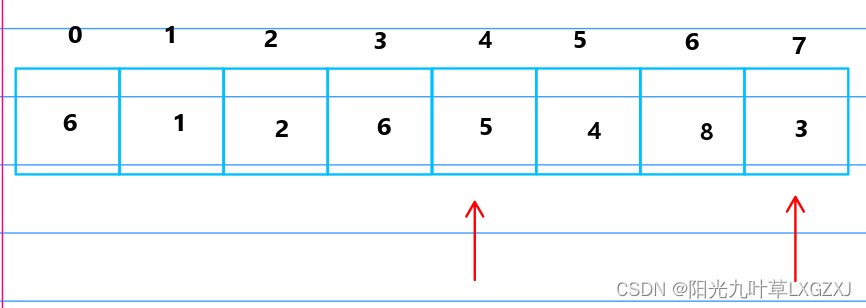

 3放到哨兵位，将5挪动到3的位置，再将哨兵的3放到原来5的位置。

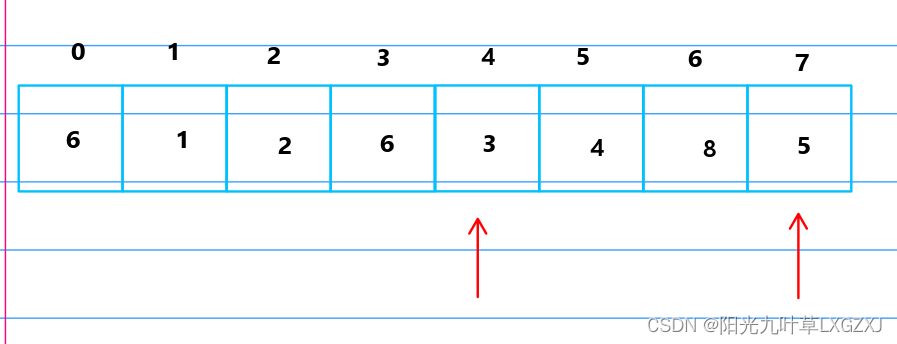 4号位的3比1号位的1大，不需要回推，3的步长排序结束了，现在开始步长为1的排序。

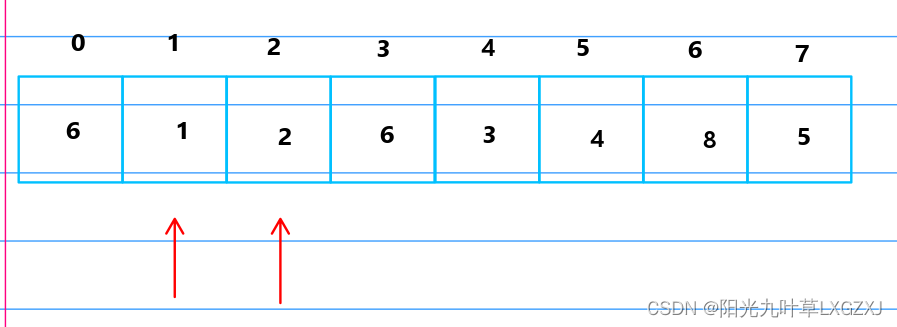
 比较1和2，发现1小于2，不需要进行排序，1号位的1前推1格超过1号位，不需要回推，前进一格。

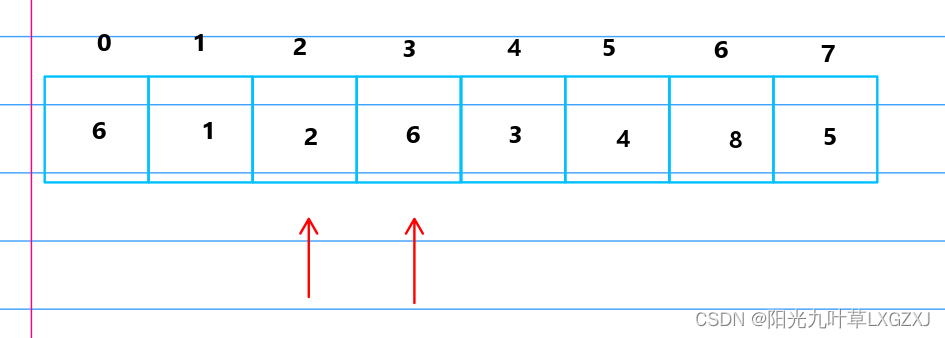
 比较2和6，发现2小于6，不需要进行排序， 2号位的2比1号位的1大，不需要回推，往后挪动一位。

比较6和3，发现6大于3，进行排序，3放到哨兵位，将6挪动到3的位置，再将哨兵的3放到原来6的位置。

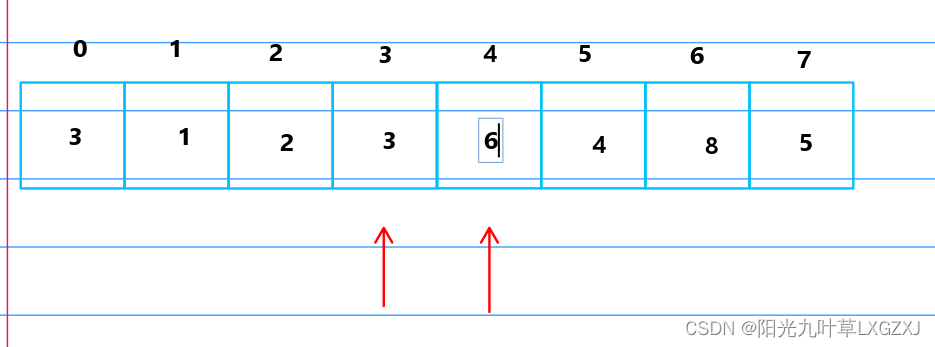
3号位的3比2号位的2大，不需要回推，往后挪动一位。

比较6和4，发现6大于4，进行排序，4放到哨兵位，将6挪动到4的位置，再将哨兵的4放到原来6的位置，4号位的4比3号位的3大，不需要回推，往后挪动一位。

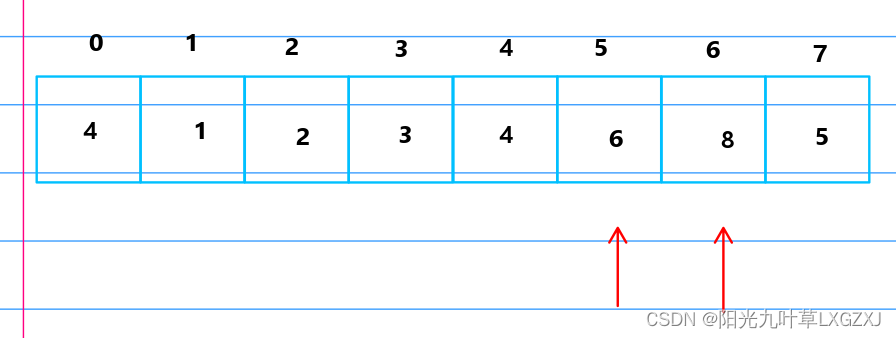
  比较6和8，发现6小于8，不需要进行排序，往后挪动一位。

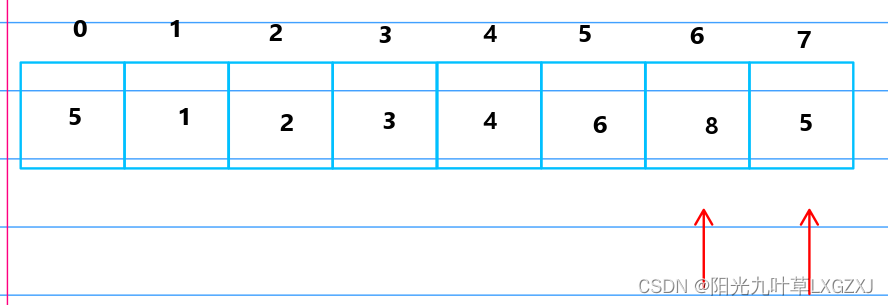
比较8和5，发现8大于5，进行排序，5放到哨兵位，将8挪动到5的位置，再将哨兵的5放到原来8的位置。

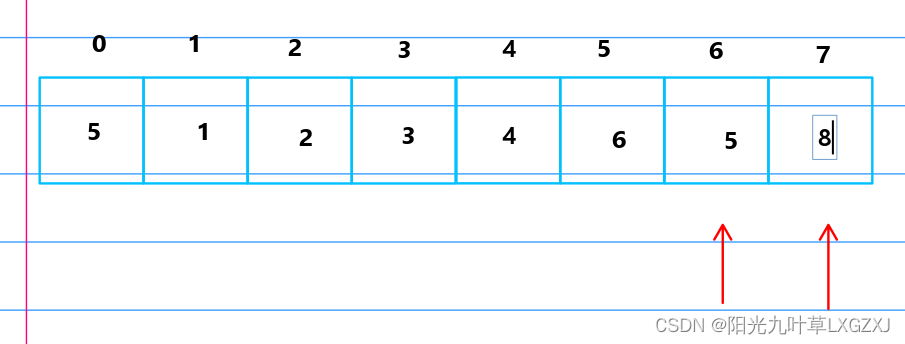
 6号位的5比5号位的6小，需要回推。

5放到哨兵位，将6挪动到5的位置，再将哨兵的5放到原来6的位置。

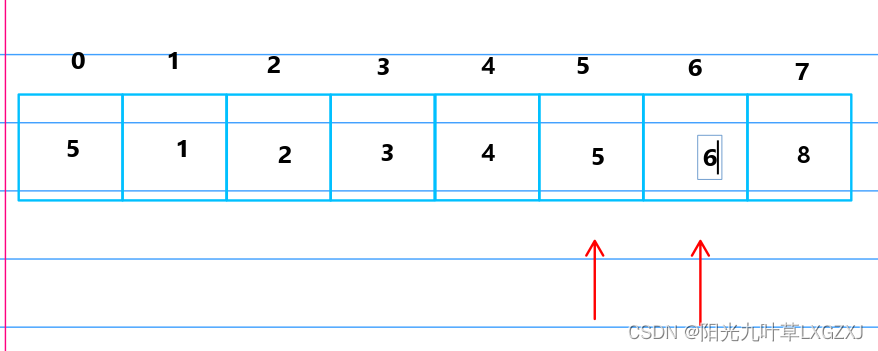
 5号位的5比4号位的4大，不需要回推，结束排序。

5、源码

（1）ShellSortSentrySqQueue

Status ShellSortSentrySqQueue(SqQueue* SortQueue)
{
    JudgeAllNullPointer(SortQueue);

    if (SortQueue->Flag != INT_TYPE_FLAG)
    {
        return FailFlag;
    }

    SqQueue*     InremrntSeqQueue = NULL;
    StepLenType  StepLen          = 0;
    QueueLenType i                = 0;
    QueueLenType j                = 0;
    QueueLenType x                = 0;
    int*         Array            = SortQueue->Data;

    InitSqQueue(&InremrntSeqQueue, INCREMENT_SEQ_MAX_LEN, INT_TYPE_FLAG);//INCREMENT_SEQ_MAX_LEN队列长度需要待商量,这边我先给了一个大致初值。
    CreateShellSortInremrntSeq(InremrntSeqQueue, SortQueue);

    for (i = GetSqQueueLen(InremrntSeqQueue) - 1; i >= 0 ; i--)
    {
        ReadSqQueue(InremrntSeqQueue,i,&StepLen);//从增量序列中读出步长。
        for (j = StepLen + 1; j < GetSqQueueLen(SortQueue); j++)
        {
            if (Array[j] < Array[j - StepLen])//当前值比减步长后的值小，说明需要交换位置。
            {
                Array[0] = Array[j];//将比较小的值，放入哨兵位。
                for ( x = j - StepLen; x > 0 && (Array[0] < Array[x]); x = x - StepLen)//j为最大限制，按照步长向左推进。
                {
                    Array[x + StepLen] = Array[x];
                }
                Array[x + StepLen] = Array[0];
                PrintfSqQueue(SortQueue,Debug);
            }
        }
    }
    
    DestroySqQueue(&InremrntSeqQueue);

    LogFormat(Debug,"Shell Sort Sentry SqQueue OK.\n");

    return SuccessFlag;
}

（2）MyIntSquare

int MyIntSquare(int Base, int Index)
{
    int i;
    int Res = 1;
    for ( i = 0; i < Index; i++)
    {
        Res *= Base;
    }
    return Res;
}

返回Base的Index次方。

（3）CreateShellSortInremrntSeq

//希尔排序增量序列的最大值为排序队列长度的二分一。（小于）
Status CreateShellSortInremrntSeq(SqQueue* InremrntSeqQueue, SqQueue* SortQueue)
{
    JudgeAllNullPointer(InremrntSeqQueue);
    JudgeAllNullPointer(SortQueue);

    StepLenType i    = 0;
    StepLenType Val  = 0;
    StepLenType Tmp  = GetSqQueueLen(SortQueue) / INCREMENT_SEQ_SPLIT_VAL;

    while (1)
    {
        Val = 9 * (MyIntSquare(4,i) - MyIntSquare(2,i)) + 1;
        if (Val > Tmp)
        {
            break;
        }
        EnterSqQueue(InremrntSeqQueue,&Val);
        i++;
    }

    PrintfSqQueue(InremrntSeqQueue,Debug);

    LogFormat(Debug,"Create Shell Sort Inremrnt Sequence OK.\n");

    return SuccessFlag;
}

创建希尔排序使用的增量序列，增量序列的算法用的是Sedgewick。

6、Linux环境编译测试

[gbase@czg2 Sort]$ time ./TestSort 
2023-8-29--[ Debug ]--Init SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,1 ,2 ,8 ,5 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Init SqQueue OK
2023-8-29--[ Debug ]--Enter SqQueue OK
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 1 ]
FrontIndex     : 0
RearIndex      : 1
SqQueueLen     : 1
SqQueueMaxLen  : 20
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Create Shell Sort Inremrnt Sequence OK.
2023-8-29--[ Debug ]--Read  SqQueue OK
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 5 ,1 ,2 ,5 ,8 ,4 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 4 ,1 ,2 ,4 ,5 ,8 ,6 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 6 ,1 ,2 ,4 ,5 ,6 ,8 ,3 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Destroy SqQueue OK
2023-8-29--[ Debug ]--Shell Sort Sentry SqQueue OK.
2023-8-29--[ Info  ]--Sort Function Elapsed Time   : 0 s
2023-8-29--[ Debug ]--SqQueue Data   :
Data           : [ 3 ,1 ,2 ,3 ,4 ,5 ,6 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 8
SqQueueMaxLen  : 8
Flag           : INT_TYPE_FLAG
2023-8-29--[ Debug ]--Destroy SqQueue OK

real    0m0.002s
user    0m0.000s
sys     0m0.002s

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/947504.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LNMT的多机部署和双机热备

LNMT的多机部署和双机热备

目录 一、环境 二、配置tomcat 三、配置nfs共享 四、配置nginx 1、两台都需要折磨配置 2、在http下面插入这两条信息 五、配置keepalived 1、安装 2、重新启动一下keepalived查看IP 六、验证双机热备 1、查看调度器备的IP&#xff0c;ip漂移说明keepalived生效 2、访…
阅读更多...
Python切换输入法的实战代码

Python切换输入法的实战代码

大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…
阅读更多...
MySQL一行记录是如何存储的？

MySQL一行记录是如何存储的？

目录 MySQL的数据存放在哪个文件&#xff1f; 表空间文件的结构是怎么样的&#xff1f; 1、行&#xff08;row&#xff09; 2、页&#xff08;page&#xff09; 3、区&#xff08;extent&#xff09; 4、段&#xff08;segment&#xff09; InnoDB 行格式有哪些&#xf…
阅读更多...
简述SpringMVC

简述SpringMVC

一、典型的Servlet JSP JavaBean UserServlet看作业务逻辑处理&#xff08;Controller&#xff09;User看作模型&#xff08;Model&#xff09;user.jsp看作渲染&#xff08;View&#xff09; 二、高级MVC 由DispatcherServlet对请求统一处理 三、SpringMVC MVC与Spr…
阅读更多...
雪花算法实现原理和精度失效问题

雪花算法实现原理和精度失效问题

一、雪花算法的实现原理 雪花算法是一个全局唯一算法&#xff0c;它主要出现在像分库分表场景中作为业务主键、 或者作为一些像订单号这类的 id 生成器。 所以单纯就全局唯一性质来说&#xff0c;有很多的实现方式&#xff0c;比如 UUID &#xff0c; Redis 的原子递增 &#…
阅读更多...
春秋云镜 CVE-2018-3191

春秋云镜 CVE-2018-3191

春秋云镜 CVE-2018-3191 Weblogic WLS Core Components 反序列化命令执行漏洞 靶标介绍 Oracle Fusion Middleware 的 Oracle WebLogic Server 组件中的漏洞&#xff08;子组件&#xff1a;WLS Core Components&#xff09;。受影响的受支持版本包括 10.3.6.0、12.1.3.0 和 1…
阅读更多...
基于Java+SpringBoot+Vue前后端分离工作流程管理系统设计和实现

基于Java+SpringBoot+Vue前后端分离工作流程管理系统设计和实现

博主介绍&#xff1a;✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ &#x1f345;文末获取源码联系&#x1f345; &#x1f447;&#x1f3fb; 精彩专…
阅读更多...
QT6为工程添加资源文件，并在ui界面引用

QT6为工程添加资源文件，并在ui界面引用

以添加图片资源为例 右键工程名字&#xff08;不是最上面的名字&#xff09;&#xff0c;点击添加现有文件 这种方式虽然添加到了工程中&#xff0c;但不能在UI设计界面完成引用。主要原因可能是未把文件放入到项目资源文件中&#xff0c;以下面一种方式可以看出区别。 点击添…
阅读更多...
clickhouse 系列2：clickhouse 离线安装

clickhouse 系列2：clickhouse 离线安装

1.下载rpm包 Altinity/clickhouse - Packages packagecloud 使用wget下载到本地目录 wget --content-disposition https://packagecloud.io/Altinity/clickhouse/packages/el/7/clickhouse-common-static-20.8.3.18-1.el7.x86_64.rpm/download.rpm wget
阅读更多...
博流RISC-V芯片JTAG debug配置与运行

博流RISC-V芯片JTAG debug配置与运行

文章目录 1、Windows下安装与配置2、Linux下安装与配置3、芯片默认 JTAG PIN 列表4、命令行运行JTAG5、Eclipse下使用JTAG 1、Windows下安装与配置 CKLink 驱动安装 Windows版驱动下载地址&#xff1a; https://occ-oss-prod.oss-cn-hangzhou.aliyuncs.com/resource//1666331…
阅读更多...
基于Java+SpringBoot+Vue前后端分离中国陕西民俗网设计和实现

基于Java+SpringBoot+Vue前后端分离中国陕西民俗网设计和实现

博主介绍&#xff1a;✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ &#x1f345;文末获取源码联系&#x1f345; &#x1f447;&#x1f3fb; 精彩专…
阅读更多...
Day49|leetcode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II

Day49|leetcode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II

leetcode 121. 买卖股票的最佳时机 题目链接&#xff1a;121. 买卖股票的最佳时机 - 力扣&#xff08;LeetCode&#xff09; 视频链接&#xff1a;动态规划之 LeetCode&#xff1a;121.买卖股票的最佳时机1_哔哩哔哩_bilibili 题目概述 给定一个数组 &#xff0c;它的第 个元…
阅读更多...
视频剪辑音效处理软件有哪些?视频剪辑软件那个好用

视频剪辑音效处理软件有哪些?视频剪辑软件那个好用

音效是视频剪辑的重要部分&#xff0c;能起到画龙点睛的作用。在短视频平台中&#xff0c;一段出彩的音效能将原本平平无奇的视频变得生动有趣。那么&#xff0c;视频剪辑音效处理软件有哪些&#xff1f;本文会给大家介绍好用的音效处理软件&#xff0c;同时也会介绍视频剪辑音…
阅读更多...
Gitee注册和使用

Gitee注册和使用

个人主页&#xff1a;点我进入主页 专栏分类&#xff1a;C语言初阶 C语言程序设计————KTV C语言小游戏 欢迎大家点赞&#xff0c;评论&#xff0c;收藏。 一起努力&#xff0c;一起奔赴大厂。 目录 1.Gitee 1.1Gitee是什么 1.2Gitee的注册以及远程仓库的创建…
阅读更多...
韦恩图的绘制matplotlib_venn模块

韦恩图的绘制matplotlib_venn模块

【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 韦恩图的绘制 matplotlib_venn模块 [太阳]选择题 请问关于以下代码说法错误是&#xff1f; import matplotlib.pyplot as plt from matplotlib_venn import venn2 s1 {1, 2, 3} s2 {3, 4, 5…
阅读更多...
2023最新 Electron.js 桌面应用开发教程（基础篇）更新中

2023最新 Electron.js 桌面应用开发教程（基础篇）更新中

Electron是什么&#xff1f; Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows上运行的跨平台应用 macOS和Linux Electron Fiddle 运行实例 Ele…
阅读更多...
Java eight 解读流(Stream)、文件(File)、IO和异常处理的使用方法

Java eight 解读流(Stream)、文件(File)、IO和异常处理的使用方法

目录 Java 流(Stream)、文件(File)和IO读取控制台输入读写文件FileInputStreamFileOutputStream Java目录 Java 异常处理 Java 流(Stream)、文件(File)和IO java.io 包几乎包含了所有操作输入、输出需要的类。所有这些流类代表了输入源和输出目标。 Java.io 包中的流支持很多种…
阅读更多...
wpf从cs代码创建简单3D物体和3D Tools研究

wpf从cs代码创建简单3D物体和3D Tools研究

前面已经说了&#xff0c;WPF项目中引入3DTools dll之后&#xff0c;在xaml中加入它的命名空间&#xff0c; xmlns:tools"clr-namespace:_3DTools;assembly3DTools" 把<Viewport3D>标签包含在<tools:TrackballDecorator>标签之中&#xff0c;就可以用鼠…
阅读更多...
Bean的生命周期和执行流程

Bean的生命周期和执行流程

文章目录 一.Bean的生命周期1.Bean的作用域2.设置Bean的作用域3.Spring的执行流程4.Bean的生命周期 一.Bean的生命周期 1.Bean的作用域 Bean的作用域指的是Bean在Spring容器中的某种行为模式,默认是singleton(单例模式)&#xff0c;一共分为6种,后四种用于spring mvc中有用 si…
阅读更多...
C++ 读写Excel LibXL库的使用附注册码（key）

C++ 读写Excel LibXL库的使用附注册码（key）

LibXL是一款用于读写处理 Excel 文件的库，支持C, C++, C#,Python等语言。并且支持多个平台windows、Linux、Mac等，它提供了一系列的API，让开发人员可以方便地读取、修改和创建Excel文件。 一、关于库的key与使用 1.价值3000多的key 但是这个库并不是免费的，使用此库需要…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023