---

一、斐波那契数列问题

1.1 题目

写一个函数，输入n，求斐波那契数列的第n项。
斐波那契数列定义如下：

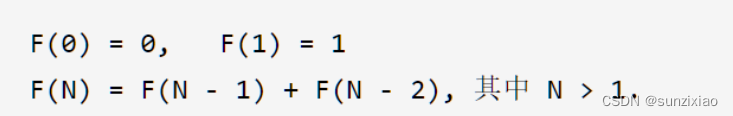
1.2 什么是斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称“兔子数列”，其数值为：1、1、2、3、5、8、13、21、34……
在数学上，这一数列以如下递推的方法定义：F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。

1.3 效率很低的解法：递归

public int Fibonacci(int n){
	if(n <= 0){
		return 0;
	}
	if(n <= 1){
		return 1;
	}
	return Fibonacci(n-1) + Fibonacci(n-2);
}

1.4 递归缺点分析

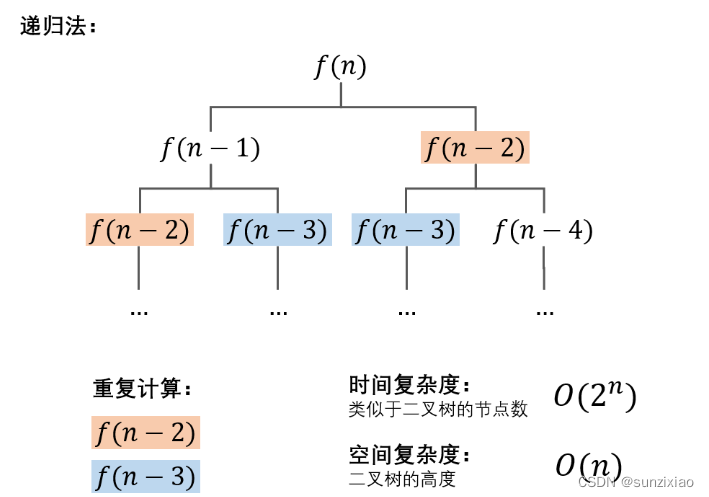
递归的代码虽然简洁，但是这并不是一个很好的解法，因为存在很严重的效率问题。
从图中可以看出，想要求f(n)，就要先求出f(n-1)和f(n-2)，同样想要求f(n-1)，就要先求出f(n-2)和f(n-3)。我们不难发现这棵树中有很多重复的节点，并且重复节点随着n增大急剧增加，这个时间复杂度以n的指数形式递增。

二、比较好的解决办法

2.1 保存数列中间项

递归之所以慢是因为重复计算太多，我们可以把已经得到的中间项保存起来，下次再使用的时候先查找，如果前面已经计算过的就不用再重复计算了。

public int Fibonacci(int n){
	int[] result = {0,1};
	if(n < 2){
		return result[n];
	}
	int[] dp = new int[n+1];
	dp[0] = 0;
	dp[1] = 1;
	for(int i = 2; i <= n; i++){
		dp[i] = dp[i-1]+dp[i-2];
	}
	return dp[n];
}

2.2 从下往上计算

更为简单的方法是从下往上计算，首先根据f(0)和f(1)算出f(2)，然后再根据f(1)和f(2)算出f(3)……
时间复杂度为f(n)。

public int Fibonacci(int n){
	int[] result = {0,1};
	if(n < 2){
		return result[n];
	}
	int p = 0;
	int q = 1;
	int res = 0;
	for(int i = 2; i <= n; i++){
		res = p + q;
		p = q;
		q = res;
	}
	return res;
}

三、公式法

public int fib(int n) {
   	double temp=Math.sqrt(5);
    double ans=(1/temp)*(Math.pow((1+temp)/2,n)-Math.pow((1-temp)/2,n));
    return (int)Math.round(ans);
    //round()函数参数为double型时，返回一个最接近该参数的long型数，参数为float型时，返回一个最接近的int值
}

这种方法的时间复杂度为O(log n)，不过公式比较生僻。

四、青蛙跳台阶问题

4.1 题目及分析

题目：
一只青蛙一次可以跳上1级台阶，也可以跳上两级台阶。求该青蛙跳上一个n级台阶总共有多少种跳法。
分析：
简单的情况：
只有一级台阶，只有一种跳法。
有两级台阶，有两种跳法：一种是跳两个一级，一种是跳一个两级。
一般情况：
跳n级台阶看成n的函数f(n)。当n>2时，第一次跳的时候有两种不同的选择，一是第一次只跳一级，跳法数目等于后面n-1级台阶的跳法数目，即f(n-1)；二是第一次跳两级，此时跳法等于后面n-2级台阶的跳法数目，即f(n-2)。因此n级台阶的跳法总数f(n) = f(n-1) + f(n-2)。可以看出这就是一个斐波那契数列。

4.2 代码实现

public int frogJump(int n){
	if(n == 1 || n == 2){
        return n;
    }
	int p = 1;
	int q = 2;
	int res = 0;
	for(int i = 3; i <= n; i++){
		res = p + q;
		p = q;
		q = res;
	}
	return res;
}