文章目录
- 2.数据的表示与计算
- 2.1 bit
- 2.1.1 信号的编码表示
- 2.1.2 计算机采用二进制的原因
- 2.1.3 数据类型
- 无符号整数
- 有符号整数
- 原码
- 反码
- 补码
- 编码方式与范围
- 移码
- 4-bit的不同编码方式
- 2.1.4 IEEE754浮点数
- 尾数
- 指数
- 0000 0000 含义
- 1111 1111含义
- 例
- 2.2 进制转换
- 2.2.1 二转十
- 2.2.2 十转二
- 2.2.3 二转十六
- 2.3 bit运算
- 2.3.1 加减法
- 符号扩展
- 溢出
- 2.3.2 逻辑运算
- 逻辑操作的描述方式——真值表
- 按位与
- 或运算
- 非运算
- 异或运算
- 应用——位矢量
- 2.4 ASCII
- 2.5 习题
2.数据的表示与计算
2.1 bit
2.1.1 信号的编码表示
一个由自然语言描述的问题,最终必须转换为计算机内部的电路工作——电子的运动,才能得以解决
在计算机内部,电子器件控制着电子的运动:监测电压大小并做出不同的响应控制。
检测电路中的电压大小会导致电路比较复杂,但只检测电路中是否有电压则很简单,会大大减低电路复杂性
从符号层面,采用 1 表示两点间存在电压;0 表示两点之间不存在电压,即二进制表示方法
0并不变时电路中绝对不存在电压,仅代表当前0所代表的电压比1代表的电压更接近电压值0- 机内将 2.9 V 2.9V 2.9V 表示为1
计算机需要定义足够大的数值范围才能工作。由于一条电路只有两个状态(1——有电压,0——无电压),为表示更多的数值状态,可以将多条线路合并使用。
通常 k k k bit宽度(k条线路)可以表示 2 k 2^k 2k 个不同的电路状态,每个状态为k个0和1的bit序列组合,称该序列为编码,每个编码对应一个特定的值与电路状态
2.1.2 计算机采用二进制的原因
- 可行性:二进制只有01两个状态,能标识01两种状态的电子器件很多。
- 运算简易性:二进制运算法则少,运算简单,简化硬件结构
- 有逻辑代数的理论基础:二进制0和1正好和逻辑代数的真假对应
其实除了可行性,其他性质都是因为采用了二进制才进而凸显的,不过为了应试,就附上吧
2.1.3 数据类型
数据类型定义了:
- 数值的表示方式(编码方式)
- 数值相关的操作方法
每个计算机指令集(ISA)都定义了一组数据类型及其相应的操作指令
- 数据类型的设计取决于ISA的设计要求
无符号整数
用于表示:执行次数,内存单元地址等没有大小意义,仅作为标记或计数的场景
k个bit可以表示 2 k 2^k 2k 个无符号整数(从 0 0 0 到 2 k − 1 2^{k}-1 2k−1)
有符号整数
在实际的算术运算中,存在着大量的负数。可以将 2 k 2^k 2k 个k-bit数分为两部分,一部分表示正数,另一部分表示负数
规定 000...000 表示数值0
计算机中,表示数值的正负需要占用一bit作为符号位,有四种数值表示方法——编码方式(二进制的不同解释方式)
原码
n+1位定点(小数点)整数范围 − 2 n − 1 ∼ 2 n − 1 -2^n-1\sim2^n-1 −2n−1∼2n−1
n+1位定点小数范围 − 1 + 2 − n ∼ 1 − 2 − n -1+2^{-n}\sim 1-2^{-n} −1+2−n∼1−2−n
- 字长足够,则可表示任意整数
- 不能表示任意小数,只能是2的整数次幂
- 真值0不唯一,可表示数少1
反码
真值0不唯一:+0,-0
表示数值的范围和原码相同
补码
n + 1 n+1 n+1 位二进制数可表示
- 定点整数 1 , 00 ⋯ 00 ⏟ n . ∼ 0 , 11 ⋯ 11 ⏟ . 1,\underbrace{00\cdots 00}_n.\sim 0,\underbrace{11\cdots 11}. 1,n 00⋯00.∼0, 11⋯11. : − 2 n ∼ 2 n − 1 -2^n \sim 2^n-1 −2n∼2n−1
- 定点小数 1. 00 ⋯ 00 ⏟ n ∼ 0. 11 ⋯ 11 ⏟ n 1.\underbrace{00\cdots00}_n\sim 0.\underbrace{11\cdots11}_n 1.n 00⋯00∼0.n 11⋯11 : − 1 ∼ 1 − 2 − n -1\sim 1-2^{-n} −1∼1−2−n
补码特点(机内码)
- 真值0的补码唯一
- 正数的补码二进制表示的无符号数,小于负数的补码表示的无符号二进制数
- 如:127:0111 1111,-1;
- 数值位1越多表示数字越大
- 0同侧编码值越大,真值越大
- 正数的2进制编码小于负数的二进制编码 1000(-8) <0111(7)
原码变为补码:从右到左,找到第一个1,其左边取反,其右边不变
原码:
01110100
补码:
10001100
\begin{aligned} &原码:0111 0100\\ &补码:1000 1100 \end{aligned}
原码:01110100补码:10001100
- 正数补码等于原码(什么编码都不变)
- 负数补码等于原码取反加一
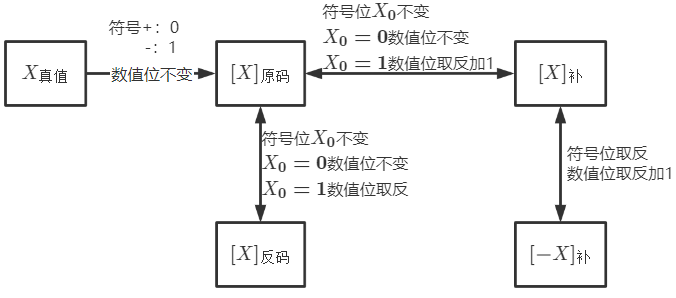
补码运算应满足的性质
-
绝对值相同但符号相反的两个数之和应为0
-
相邻两个码字之间相差为00…001
REPRESENTATION(value+1)=REPRESENTATION(value)+REPRESENTATION(1)
在计算机中,完成加法运算的是ALU,他是一种计算机制 ,只会对二进制数进行加法操作,而不考虑其他因素(正数、负数或加法累计效果),即 策略 由上层指定
具体运算策略见组成原理对这部分的解释
编码方式与范围
n位2进制编码
| 编码方式 | 最小值编码 | 最小值 | 最大值编码 | 最大值 | 数值范围 |
|---|---|---|---|---|---|
| 无符号定点整数 | 00...00 ⏟ n . \underbrace{00...00}_n. n 00...00. | 0 | 11...11 ⏟ n . \underbrace{11...11}_n. n 11...11. | 2 n + 1 − 1 2^{n+1}-1 2n+1−1 | 0 ≤ x ≤ 2 n + 1 − 1 0\le x\le 2^{n+1}-1 0≤x≤2n+1−1 |
| 无符号定点小数 | . 00...00 ⏟ n .\underbrace{00...00}_n .n 00...00 | 0 | 0. 11...11 ⏟ n 0.\underbrace{11...11}_n 0.n 11...11 | 1 − 2 − n 1-2^{-n} 1−2−n | 0 ≤ x ≤ 1 − 2 − n 0\le x\le 1-2^{-n} 0≤x≤1−2−n |
| 原码定点整数 | 1 , 1...11 ⏟ n − 1 . 1,\underbrace{1...11}_{n-1}. 1,n−1 1...11. | − 2 n + 1 -2^n+1 −2n+1 | 0 , 1 ⋯ 11 ⏟ n − 1 . 0,\underbrace{1\cdots11}_{n-1}. 0,n−1 1⋯11. | 2 n − 1 2^n-1 2n−1 | − 2 n + 1 ≤ x ≤ 2 n − 1 -2^n+1\le x \le 2^n-1 −2n+1≤x≤2n−1 |
| 原码定点小数 | 1. 1...11 ⏟ n − 1 1.\underbrace{1...11}_{n-1} 1.n−1 1...11 | − 1 + 2 − n -1+2^{-n} −1+2−n | 0. 1...11 ⏟ n − 1 0.\underbrace{1...11}_{n-1} 0.n−1 1...11 | 1 − 2 − n 1-2^{-n} 1−2−n | − 1 − 2 − n ≤ x ≤ 1 − 2 − n -1-2^{-n}\le x \le 1-2^{-n} −1−2−n≤x≤1−2−n |
| 补码定点整数 | 1 , 0...00 ⏟ n − 1 . 1,\underbrace{0...00}_{n-1}. 1,n−1 0...00. | − 2 n -2^n −2n | 0 , 1...11 ⏟ n − 1 . 0,\underbrace{1...11}_{n-1}. 0,n−1 1...11. | 2 n − 1 2^n-1 2n−1 | − 2 n ≤ x ≤ 2 n − 1 -2^n\le x \le 2^n-1 −2n≤x≤2n−1 |
| 补码定点小数 | 1. 0...00 ⏟ n − 1 1.\underbrace{0...00}_{n-1} 1.n−1 0...00 | − 1 -1 −1 | 0. 1...11 ⏟ n − 1 0.\underbrace{1...11}_{n-1} 0.n−1 1...11 | 1 − 2 − n 1-2^{-n} 1−2−n | − 1 ≤ x ≤ 1 − 2 − n -1\le x \le 1-2^{-n} −1≤x≤1−2−n |
移码
真值加一个常数
[ x ] 移 = 2 n + x ( − 2 n ≤ x ≤ 2 n ,机器字长为 n + 1 ) x 1 = + 10101 , x 2 = − 10101 ,字长 8 位,则其移码表示为: [ x 1 ] 移 = 2 7 + 10101 = 1 , 0010101 , [ x 2 ] 移 = 2 7 + ( − 10101 ) = 0 , 1101011 \begin{aligned} &[x]_移=2^n+x(-2^n\le x \le 2^n,机器字长为n+1)\\ &x_1=+10101,x_2=-10101,字长8位,则其移码表示为:\\ &[x_1]_移=2^7+10101=1,0010101,[x_2]_移=2^7+(-10101)=0,1101011 \end{aligned} [x]移=2n+x(−2n≤x≤2n,机器字长为n+1)x1=+10101,x2=−10101,字长8位,则其移码表示为:[x1]移=27+10101=1,0010101,[x2]移=27+(−10101)=0,1101011
- 只能表示整数
- 真值0唯一
- 二进制编码越大,所表示的数值越大
- 移码大,真值大
- 移码小,真值小
n位二进制能表示 2 n 2^n 2n 个数字
移码一般是加10…01 ,即编码表示的无符号整数减去 2 n − 1 2^{n}-1 2n−1
4-bit的不同编码方式
| 二进制 | 原码 | 反码 | 补码 | 移码+1001 |
|---|---|---|---|---|
| 0000 | 0 | 0 | 0 | -7 |
| 0001 | 1 | 1 | 1 | -6 |
| 0010 | 2 | 2 | 2 | -5 |
| 0011 | 3 | 3 | 3 | -4 |
| 0100 | 4 | 4 | 4 | -3 |
| 0101 | 5 | 5 | 5 | -2 |
| 0110 | 6 | 6 | 6 | -1 |
| 0111 | 7 | 7 | 7 | 0 |
| 1000 | -0 | -7 | -8 | 1 |
| 1001 | -1 | -6 | -7 | 2 |
| 1010 | -2 | -5 | -6 | 3 |
| 1011 | -3 | -4 | -5 | 4 |
| 1100 | -4 | -3 | -4 | 5 |
| 1101 | -5 | -2 | -3 | 6 |
| 1110 | -6 | -1 | -2 | 7 |
| 1111 | -7 | -0 | -1 | 8 |
2.1.4 IEEE754浮点数
浮点数可以表示很大的数值,也可以表示很小的数值,只是牺牲一些数值精度而已
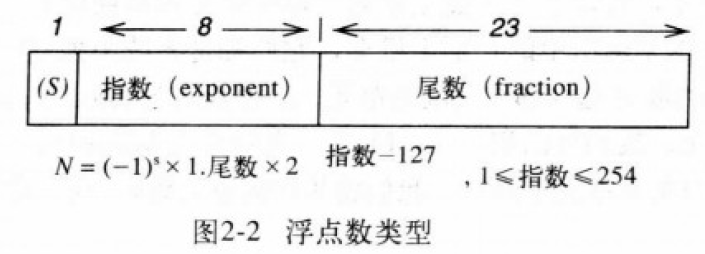
符号位:1bit,表示数值的正负
数值范围:8bit,代表范围(指数,exponent)
数值精度:23bit,代表精度(位数部分,fraction)
尾数
准确的,不存在任何误差的bit的位数为精度
在IEEE中,尾数是正则化的,即小数点左边有且仅有一个非零数
在二进制下, 正则化的尾数为 1.xxxxx
即用23bit尾数就可表示24位精度
指数
8-bit的二进制数可表示255个无符号整数,在IEEE中,指数值范围为
−
126
∼
126
-126\sim 126
−126∼126 ,剩余的两个指数 00000000 和 11111111 有特殊含义
指数部分为移码
- 实际的指数值等于该无符号整数减127之后的结果——相当于加
1000 0001
| 二进制 | 指数值 |
|---|---|
| 0000 0000 | 特殊含义 |
| 0000 0001 | -126 |
| … … | … … |
| 0111 1111 | 0 |
| 1000 0000 | 1 |
| … … | … … |
| 1111 1110 | 126 |
| 1111 1111 | 特殊含义 |
0000 0000 含义
表示指数值为-126,但尾数不是正规化的
- 尾数全0
0...0,则为0 - 尾数非0,则该浮点数的值为 ( − 1 ) s × 0. 尾数 × 2 − 126 (-1)^s\times 0.尾数\times 2^{-126} (−1)s×0.尾数×2−126
1111 1111含义
- 尾数全0,无穷大
- 尾数不全为0,非数值
例
用IEEE浮点数标准表示 − 6 5 8 -6\frac{5}{8} −685
符号位为1
5 8 = . 101 \frac{5}{8}=.101 85=.101, 6 = 110 6=110 6=110 —— 110.101 110.101 110.101 正则化后为 1.10101 × 2 2 1.10101\times 2^{2} 1.10101×22
指数部分 2+127=0000 0010+0111 1111=1000 0001
故 IEEE的浮点数表示为:1 1000 0001 101 0100 0000 0000 0000 0000
IEEE浮点数0 0111 1011 00000000000000000000000表示什么数
符号位s=0,表示整数
指数部分:0111 1011 -127 为
123
−
127
=
−
4
123-127=-4
123−127=−4
尾数部分:1.0xxx0
所以该二进制数表示 + 1.0 × 2 − 4 +1.0\times 2^{-4} +1.0×2−4
2.2 进制转换
2.2.1 二转十
a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0
-
8bit补码数据,最高位 a 7 a_7 a7 为符号位
-
为0,则直接进行第二步转换 a 6 ′ a 5 ′ a 4 ′ a 3 ′ a 2 ′ a 1 ′ a 0 ′ = a 6 a 5 a 4 a 3 a 2 a 1 a 0 a'_{6}a'_{5}a'_{4}a'_{3}a'_{2}a'_{1}a'_{0}=a_6a_5a_4a_3a_2a_1a_0 a6′a5′a4′a3′a2′a1′a0′=a6a5a4a3a2a1a0
-
为1,需要转换为绝对值相等的正数——取反+1
a 6 ′ a 5 ′ a 4 ′ a 3 ′ a 2 ′ a 1 ′ a 0 ′ = a 6 a 5 a 4 a 3 a 2 a 1 a 0 ‾ + 1 a'_{6}a'_{5}a'_{4}a'_{3}a'_{2}a'_{1}a'_{0}=\overline{a_6a_5a_4a_3a_2a_1a_0}+1 a6′a5′a4′a3′a2′a1′a0′=a6a5a4a3a2a1a0+1
-
-
x = a 6 ′ × 2 6 + a 5 × 2 5 + a 4 × 2 4 + a 3 × 2 3 + a 2 × 2 2 + a 1 × 2 1 + a 0 × 1 x=a^{'}_6\times 2^6+a_5 \times 2^5+a_4\times 2^4+a_3 \times 2^3+a_2\times 2^2+a_1 \times 2^1+a_0\times 1 x=a6′×26+a5×25+a4×24+a3×23+a2×22+a1×21+a0×1
-
若为负数,加上负号即可
2.2.2 十转二
-
将十进制数N展开为2次幂的求和
N = a 6 × 2 6 + a 5 × 2 5 + a 4 × 2 4 + a 3 × 2 3 + a 2 × 2 2 + a 1 × 2 1 + a 0 × 2 0 N=a_6\times 2^6+a_5\times 2^5+a_4\times 2^4+a_3\times 2^3+a_2\times 2^2+a_1\times 2^1+a_0\times 2^0 N=a6×26+a5×25+a4×24+a3×23+a2×22+a1×21+a0×20
反复执行一下操作,直至N变为0
- 如果N为奇数,则左边最低位 a i a_i ai 为1。如果N为偶数,则左边最低位 a i a_i ai 为0
- 即将等式两端同时减1(奇数)或0(偶数),消除最低位后,将等式两端同时除以2
每执行一次,可以求得一个 a i a_i ai 的值
-
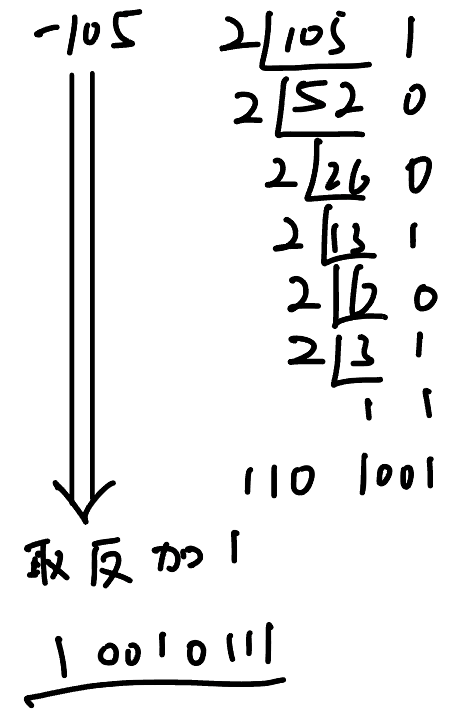
如果N值为正,则 a 7 a_7 a7 取值为0
-
如果N值为负,则最高位补0,然后求该编码的补码,完成
和手算的取余,然后逆序一样
2.2.3 二转十六
适合计算机计算且方便人阅读
一个16bit的二进制数 a 15 a 14 a 13 a 12 a 11 a 10 a 9 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_{15}a_{14}a_{13}a_{12}a_{11}a_{10}a_{9}a_{8}a_{7}a_{6}a_{5}a_{4}a_{3}a_{2}a_{1}a_{0} a15a14a13a12a11a10a9a8a7a6a5a4a3a2a1a0
其相应的无符号整数表示为
2
15
×
a
15
+
2
14
×
a
14
+
2
13
×
a
13
+
2
12
×
a
12
+
2
11
×
a
11
+
2
10
×
a
10
+
2
9
×
a
9
+
2
8
×
a
8
+
2
7
×
a
7
+
2
6
×
a
6
+
2
5
×
a
5
+
2
4
×
a
4
+
2
3
×
a
3
+
2
2
×
a
2
+
2
1
×
a
1
+
2
0
×
a
0
\begin{aligned} &2^{15}\times a_{15}+2^{14}\times a_{14}+2^{13}\times a_{13}+2^{12}\times a_{12}+2^{11}\times a_{11}+2^{10}\times a_{10}+2^{9}\times a_{9}+2^{8}\times a_{8}+\\ &2^{7}\times a_{7}+2^{6}\times a_{6}+2^{5}\times a_{5}+2^{4}\times a_{4}+2^{3}\times a_{3}+2^{2}\times a_{2}+2^{1}\times a_{1}+2^{0}\times a_{0} \end{aligned}
215×a15+214×a14+213×a13+212×a12+211×a11+210×a10+29×a9+28×a8+27×a7+26×a6+25×a5+24×a4+23×a3+22×a2+21×a1+20×a0
从低位到高位,每四位为一组
2
12
×
[
2
3
×
a
15
+
2
2
×
a
14
+
2
1
×
a
13
+
2
0
×
a
12
]
+
2
8
×
[
2
3
×
a
11
+
2
2
×
a
10
+
2
1
×
a
9
+
2
0
×
a
8
]
+
2
4
×
[
2
3
×
a
7
+
2
2
×
a
6
+
2
1
×
a
5
+
2
0
×
a
4
]
+
2
0
×
[
2
3
×
a
3
+
2
2
×
a
2
+
2
1
×
a
1
+
2
0
×
a
0
]
=
1
6
3
×
h
3
+
1
6
2
×
h
2
+
1
6
1
×
h
1
+
1
6
0
×
h
0
\begin{aligned} 2^{12}\times [2^3\times a_{15}+2^{2}\times a_{14}+2^1\times a_{13}+2^{0}\times a_{12}]\\ +2^{8}\times [2^3\times a_{11}+2^{2}\times a_{10}+2^1\times a_{9}+2^{0}\times a_{8}]\\ +2^{4}\times [2^3\times a_{7}+2^{2}\times a_{6}+2^1\times a_{5}+2^{0}\times a_{4}]\\ +2^{0}\times [2^3\times a_{3}+2^{2}\times a_{2}+2^1\times a_{1}+2^{0}\times a_{0}]\\ =16^3\times h_3+16^2\times h_2+16^1\times h_1+16^0\times h_0 \end{aligned}
212×[23×a15+22×a14+21×a13+20×a12]+28×[23×a11+22×a10+21×a9+20×a8]+24×[23×a7+22×a6+21×a5+20×a4]+20×[23×a3+22×a2+21×a1+20×a0]=163×h3+162×h2+161×h1+160×h0
由于
h
i
h_i
hi 共有16种取指(
0
∼
15
0\sim 15
0∼15) ,用符号
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
A
,
B
,
C
,
D
,
E
,
F
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 作为
h
i
h_i
hi 的值
- 0表示 0000 0000 0000
- 1表示 0001 0001 0001
- A表示 1010 1010 1010
- F表示 1111 1111 1111
十六进制的主要好处在于方便记忆和使用。避免了因二进制数字串过长引起的誊写错误
2.3 bit运算
2.3.1 加减法
二进制加法与十进制加法相同,从右向左将两数按列对齐并依次相加;如果前列的加法产生进位,则该进位bit参加左边列的加法操作
11+3
01011
00011
−
−
01110
\begin{aligned} &01011\\ &00011\\ &--\\ &01110\\ \end{aligned}
0101100011−−01110
减法理解为加负数, A − B = A + ( − B ) A-B=A+(-B) A−B=A+(−B)
14-9(01001)
01110
10111
−
−
00101
\begin{aligned} &01110\\ &10111\\ &--\\ &00101 \end{aligned}
0111010111−−00101
加本数相当于乘2,在位运算相当于左移1为
x + x ⟺ x < < 1 x+x\iff x<<1 x+x⟺x<<1
符号扩展
将两个长度不等的二进制相加,需要进行对齐操作——符号扩展
补码运算 (Sign Extension,简称SEXT)
- 正数前0扩展不改变原值
- 负数前1扩展不改变原值

溢出
运算结果超出编码的最大值或最小值的情况
无符号整数溢出情况:最高位发生进位
有符号整数溢出情况:
- 正数与正数相加
- 负数与负数相加
2.3.2 逻辑运算
对两个长度为 m-bit 的二进制数做逻辑运算,将两个操作数按位对齐,然后对其中每一对bit进行运算,称为按位逻辑操作
- 只影响本位,不是算术运算,所以没有进位
作用:
-
判断某位的取值(0/1)
- 当判断最后一位是0或是1时,可判断二进制表示数值的奇偶
-
取出二进制数的某一位
-
某位置为0/1
-
位取反——非运算
-
用于比较两数是否相等——异或
逻辑操作的描述方式——真值表
对于n个操作数的逻辑操作,构造
- 行数——
2
n
2^n
2n
- n个操作数的可能组合数为 2 n 2^n 2n 种
- 列数——
n
+
1
n+1
n+1
- 前n列表示n个源操作数
- 最后一列表示该组合方式下逻辑运算的结果
的真值表
按位与
全1得1,有0得0
a=0011101001101001
b=0101100100100001
a&b=
0001100000100001
与运算作用:
位置0 :与0
-
应用:计算n二进制的个数—— 每步使最低位的1变0
n=n&(n-1);count++;直至n==0减法,向最低可进位借1,改为变为0,与减1之后的数相与,可将最低可借位和低位置0,高位不变
判断某位取值 :与1
取特定位 :屏蔽字位:两部分组成
- 关心的位——目标位取1
- 忽略的位——其余为0
作用是将关心的位提出来——取某位
如取出8-bit数据A的低2位,其屏蔽字为 0000 0011 ,无论A取何值,与屏蔽字与的结果必然是 00000000 、00000001 、00000010 、00000011 中的一个
或运算
全0得0,有1得1
a=0011101001101001
b=0101100100100001
a|b=
0111101101101001
与运算作用:
位置1 :或1
判断某位取值 :或1
非运算
按位取反
a=0011101001101001
~a=
1100010110010110
异或运算
按位异或
异或真值表
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
- 两个输入值不同,则输出为1
- 两个输入值相同,则输出为0
a=0011101001101001
b=0101100100100001
a^b=
0110001101001000
用于判断两个二进制数是否相同
- 若两个数相等,则异或之后为0
应用——位矢量
在复杂系统中,包含了很多独立单元,每个单元或忙或空闲。
假设存在n个单元,可以用一个 n-bit 的二进制数代表这n个单元。
- 当某个单元忙碌时,将相应的bit置1——
|0...010...0 - 当某个单元空闲时,将相应的bit置0——
&1...101...1
2.4 ASCII
用于在计算机处理单元和IO设备之间传递字符的8-bit编码标准。
键盘上每个键位一般不止对应一个ASCII码
- 通过功能键
shift切换
每次按键都会产生唯一的ASCII码
2.5 习题
2.5.1 一个n-bit二进制数可表示 2 n 2^n 2n 个不同的二进制数
2.5.2
用二进制bit串表示26个英文字母,需要 ⌈ l o g 2 26 ⌉ = 5 \lceil log_226\rceil=5 ⌈log226⌉=5 bit,区分大小需要 2 × ⌈ l o g 2 26 ⌉ = 6 2\times \lceil log_226\rceil=6 2×⌈log226⌉=6 bit

⌈ l o g 2 400 ⌉ = 9 \lceil log_2400\rceil=9 ⌈log2400⌉=9 bit
2 9 − 400 = 112 2^9-400=112 29−400=112 个
2.5.4 给定n-bit,可表示多少无符号整数,范围多大
可表示 2 n 2^n 2n 个无符号整数,范围为 0 ∼ 2 n − 1 0\sim 2^n-1 0∼2n−1
2.5.5 用5-bit二进制串表示数值,写出7和-7的反码,符号位码和补码表示
| 原码 | 反码 | 补码 | |
|---|---|---|---|
| 7 | 00111 | 00111 | 00111 |
| -7 | 10111 | 11000 | 11001 |
2.5.6 用6-bit补码表示32
100000
**2.5.7 ** 列出4-bit二进制补码能表示的所有整数
| 补码 | 数值 |
|---|---|
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |

a. 2 ( 8 − 1 ) − 1 = 2 7 − 1 = 127 2^{(8-1)}-1=2^7-1=127 2(8−1)−1=27−1=127 , 0111 1111
b. 可表示绝对值最大的负数为 − 2 7 = − 128 -2^7=-128 −27=−128 ,其二进制数表示为 10000000 1000 0000 10000000
c. 2 n − 1 − 1 2^{n-1}-1 2n−1−1
d. − 2 n − 1 -2^{n-1} −2n−1
2.5.9 如果用二进制补码方式表示摩尔常数 6.0 × 1 0 23 6.0\times 10^{23} 6.0×1023 ,需要多少bit?
2 n ≥ 6 × 1 0 23 ⇒ l o g 2 n ≥ l o g 2 ( 6 × 1 0 23 ) ⇒ n ≥ 79 2^n\ge 6\times 10^{23}\Rightarrow log_2n\ge log_2(6\times 10^{23})\Rightarrow n\ge 79 2n≥6×1023⇒log2n≥log2(6×1023)⇒n≥79
需要1-bit作为符号位,所以共需要 80-bit

a. 1010 = 取反 + 1 1110 = − 6 1010\overset{取反+1}{=}1110=-6 1010=取反+11110=−6
b. 2 1 + 2 3 + 2 4 + 2 6 = 64 + 16 + 8 + 2 = 90 2^1+2^3+2^4+2^6=64+16+8+2=90 21+23+24+26=64+16+8+2=90
c. 11111110 = 取反至最低 1 10000010 = − 2 11111110\xlongequal{取反至最低1}10000010=-2 11111110取反至最低110000010=−2
d. 0011100111010011 = 14803 0011100111010011=14803 0011100111010011=14803
2.5.11 十进制数转为8-bit补码
a. 102=64+32+4+2=0110 0110
b. 64=0100 0000
c. 33=32+1=0010 0001
d. -128 = 1000 0000
e. 127=0111 1111

可被4整除的偶数
2.5.13 将二进制数改为8-bit数,且不允许改变原值
a. 1010——1111 1010
b. 011001——0001 1001
c. 1111111000——1111 1000
d. 01——0000 0001
2.5.14 二进制数加法
a. 1011+0001=1100
b. 0000+1010=1010
c. 1100+0011=1111
d. 0101+0110=1011
e. 1111+0001=1,0000,发生溢出
2.5.15 左移一位等价于乘2,右移一位等价于除2

a. 7的反码:0000 0111 -7的反码:1111 1000,相加为 1111 1111:-0的反码
b. 7的原码:0000 0111 -7的原码:1000 0111,相加为 1000 1110:-14
c. 7的补码:0000 0111 -7的补码:1111 1001,相加为 0000 0000:0
2.5.17 计算补码加法,并将结果转换为十进制数
a. 01+1011=0001+1011=1100:12
b. 11+01010101=0000 0011 + 0101 0101 = 0101 1000:88
c. 0101+110=0101+1110=0011:3
d. 01+10=11=-1
补码计算注意符号位扩展
2.5.18 计算无符号二进制加法,并将结果转换为十进制
a. 01+1011=1100 :12
b. 11+01010101=1011000:88
c. 0101+110=1011 :11
d. 01+10=11 :3
2.5.19 将十进制数 -27 分别转换为8-bi补码,16-bit补码,32-bit补码,并阐述符号位扩展在这三种表达方式中的应用
-27的二进制形式:1110 0101 ,补码符号位扩展 16-bit 1111 1111 1110 0101 ,32-bit
11
⋯
11
⏟
24
11100101
\underbrace{11\cdots 11}_{24} 1110 0101
24
11⋯1111100101
2.5.20 4-bit补码运算溢出,改为十进制验证
a. 1100+0011=1111 :-1,不会发生溢出
-4+3=-1
b. 1100+0100=0000 :0,不会发生溢出
-4+4=0
c. 0111+0001=1000 :-8,发生溢出
7+1=8
d. 1000-0001=1000+1111=0111 :7,发生溢出
-8-1=-9
e. 0111 + 1001 = 0000 :0,不会发生溢出
7±7=0
2.5.21 补码相加发生溢出情况:两个正数或两个负数相加才可能发生溢出
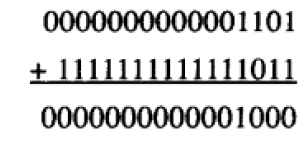
2.5.22 两个16-bit补码相加溢出的例子
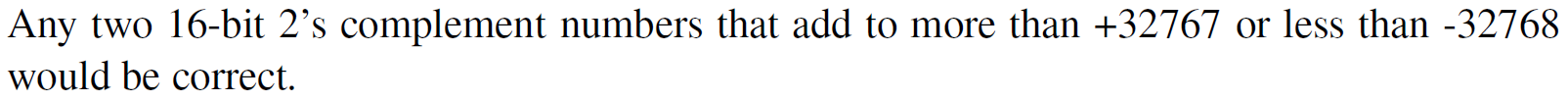
2.5.23 两个无符号整数相加会溢出的情况:最左bit发生进位是发生溢出
2.5.24 两个16-bit无符号整数相加溢出的例子

2.5.25 为什么在补码方式下负数和正数相加并不会溢出
对于正数,运算后其结果一定小于正加数
对于负数,运算后其结果一定大于负加数

a. ⌈ l o g 2 64 ⌉ = 6 \lceil log_264\rceil=6 ⌈log264⌉=6 ,需要增加1bit符号位,所以最少需要7bit
b. 最大正整数 001 1111 = 63
c. 最大无符号整数:111 1111 = 127

发生了溢出,两个正数补码相加,结果应为正数。由于发生溢出,结果为负数
2.5.28 And逻辑运算什么条件为1
2输入为1时,And逻辑运算为1
2.5.29
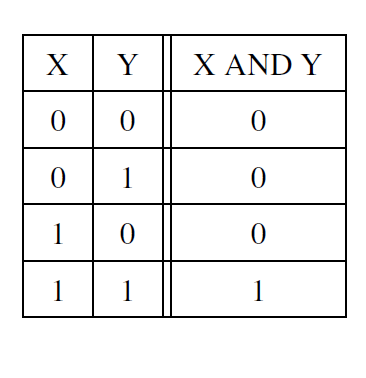

a. 0101 0111 & 1101 0111 = 0101 0111
b. 101 & 110 = 100
c. 1110 0000 & 1011 0100 = 1010 0000
d. 0001 1111 & 1011 0100 = 0001 0100
e. (0011 & 0110) & 1101 = 0010 & 1101 = 0000
f. 0011 & (0110 & 1101) = 0011 & 0100 = 0000
2.5.31 什么情况下OR逻辑运算为1
2.5.32
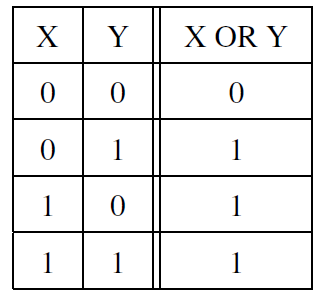
2.5.33
a. 0101 0111 | 1101 0111 = 1101 0111
b. 101 | 110 = 111
c. 1110 0000 | 1011 0100 = 1111 0100
d. 0001 1111 | 1011 0100 = 1011 1111
e. (0101 | 1100) | 1101 = 1101 | 1101 = 1101
f. 0101 | (1100 | 1101) = 0101 | 1101 = 1101
2.5.34
a. !(1011) | !(1100) = 0100 | 0011 = 0111
b. !(1000 & (1100 | 0101)) = !(1000 & 1101) = !1000 = 0111
c. !(!1101)=1101
d. (0110 | 0000) & 1111 = 0110 & 1111 = 0110
2.5.35 屏蔽字作用
修改设备状态:
- 置1:设为空闲
- 置0:设为忙碌
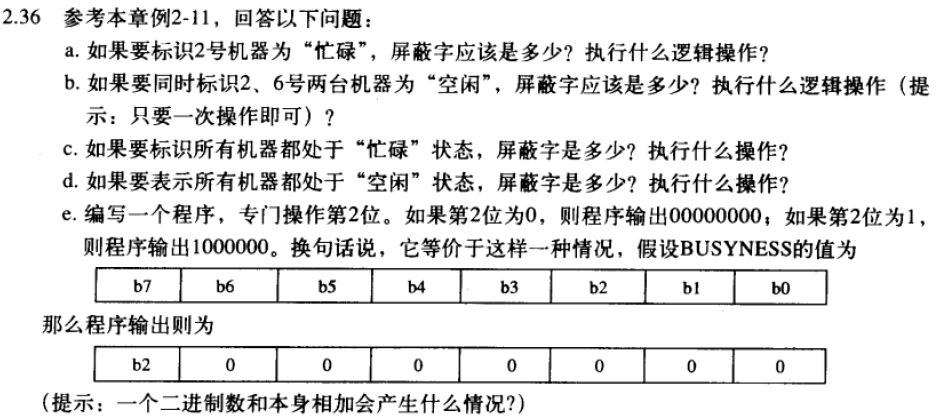
a. &1111 1011
b. | 0100 0100
c. &0000 0000
d. | 1111 1111
e. &0000 0100,左移5位

加法器符号位溢出判断 V=(n&m&!s) | (!n &!m&s)&1000
若V=1000,则溢出
若V=0000,则无溢出

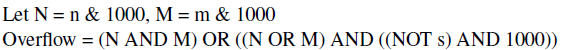
V=n&m&1000+(n+m)&!s&1000=(n&m+(n+m)&!s)&1000
- 一定不溢出:n与m都是0xxx , n + m = s < 2 4 − 1 n+m=s<2^4-1 n+m=s<24−1
2.5.39 将十进制数转化为IEEE格式浮点数
a. 3.75 11.11 1.111 × 2 1 1.111\times 2^1 1.111×21 尾数为 . 111 00 ⋯ 0 ⏟ 20 .111 \underbrace{00\cdots0}_{20} .11120 00⋯0 ,移码为 1 + 127 = 10000000 1+127=1000 0000 1+127=10000000 ,符号位为0
b.
−
55
23
64
=
−
(
32
+
16
+
4
+
2
+
1
+
16
+
4
+
2
+
1
64
)
=
−
110111.010111
=
−
1.1011010101
×
2
00000101
-55\frac{23}{64}=-(32+16+4+2+1+\frac{16+4+2+1}{64})=-110111.010111=-1.1011010101\times 2^{0000 0101}
−556423=−(32+16+4+2+1+6416+4+2+1)=−110111.010111=−1.1011010101×200000101
尾数为
.
10111010111
00
⋯
00
⏟
12
.101 1101 0111 \underbrace{00\cdots00}_{12}
.1011101011112
00⋯00 ,移码为
5
+
127
=
01111111
+
00000101
=
10000100
5+127=0111 1111 +0000 0101=1000 0100
5+127=01111111+00000101=10000100,符号为 1
c. 3.1415927
d. 64000 = 32768+16384+8192+4096+2048+512
1111101000000000
=
1.111101
×
2
00001111
1111101000000000=1.111101\times 2^{0000 1111}
1111101000000000=1.111101×200001111
尾数为
111101
00
⋯
00
⏟
17
111101\underbrace{00\cdots00}_{17}
11110117
00⋯00 ,阶码为
15
+
127
=
00001111
+
01111111
=
10001110
15+127=0000 1111+0111 1111=10001110
15+127=00001111+01111111=10001110
2.5.40 IEEE转换为十进制数
| 编号 | 符号位 | 数符 | 阶码 | 指数 | 尾数 | 小数部分 | 二进制数 | 十进制数 |
|---|---|---|---|---|---|---|---|---|
| a | 0 | 正数 | 10000000 | 1 | 00 ⋯ 0 ⏟ 23 \underbrace{00\cdots 0}_{23} 23 00⋯0 | 1.0 | 1.0 × 2 1 1.0\times 2^1 1.0×21 | 2 |
| b | 1 | 负数 | 10000011 | 4 | 0001 00 ⋯ 0 ⏟ 19 0001\underbrace{00\cdots 0}_{19} 000119 00⋯0 | 1.0001 | - 1.0001 × 2 4 1.0001\times 2^{4} 1.0001×24 | -17 |
| c | 0 | . | 11111111 | . | 00 ⋯ 0 ⏟ 23 \underbrace{00\cdots0}_{23} 23 00⋯0 | . | . | 无穷 |
| d | 1 | 负数 | 10000000 | 1 | 1001 00 ⋯ 0 ⏟ 19 1001\underbrace{00\cdots 0}_{19} 100119 00⋯0 | 1.1001 | 1.1001 × 2 1 1.1001\times 2^{1} 1.1001×21 | − 1.5625 -1.5625 −1.5625 |
2.5.41
a. 32-bit IEEE浮点数能表示的最大数值是多少?
阶码最大为 1111 1110 ,指数最大为126,尾数最大为
11
⋯
1
⏟
23
\underbrace{11\cdots1}_{23}
23
11⋯1 ,小数部分为
1.
11
⋯
1
⏟
23
1.\underbrace{11\cdots1}_{23}
1.23
11⋯1 ,其十进制数表示为
(
2
−
2
−
23
)
×
2
126
(2-2^{-23})\times 2^{126}
(2−2−23)×2126
b. 32-bit IEEE 浮点数能表示的最小数值是多少?
阶码最小为 0000 0001 ,指数最小为-126,尾数最小为
00
⋯
0
00\cdots 0
00⋯0,小数部分为
1.
00
⋯
0
⏟
23
1.\underbrace{00\cdots 0}_{23}
1.23
00⋯0 ,其十进制数为
−
1.0
×
2
−
126
-1.0\times 2^{-126}
−1.0×2−126

ASCII码
| 字符 | 十进制数 | ASCII |
|---|---|---|
| 0 | 48 | 0011 0000 |
| 5 | 53 | 0011 0101 |
| 8 | 56 | 0011 1000 |
| A | 65 | 0100 0001 |
| Z | 90 | 0101 1010 |
| a | 97 | 0110 0001 |
| m | 109 | 0110 1101 |
| z | 122 | 0111 1010 |

a. x48656c6c6f21
x48-0100 1000-72-H
x65-0110 0101-101-e
x6c-0110 1100-108-l
x6f-0110 1111-111-o
x21-0010 0001-33-!


3的二进制数为0000 0011,其ASCII为0011 0011
假设待转换的数值为n,其二进制B表示为 00000000 ∼ 00001001 0000 0000\sim 0000 1001 00000000∼00001001 ,表示为ASCII的二进制数为A
由于 ‘0’ 的ASCII为 0110 0000,所以B转为A,只需要将高四位变为 0110 ,即ASCII码B的十进制数与数值n关系:B=n+48
2.5.45 二进制转十六进制
a. 1101 ⏟ D 0001 ⏟ 1 1010 ⏟ A 1111 ⏟ F \underbrace{1101}_{D} \underbrace{0001}_1 \underbrace{1010}_A \underbrace{1111}_F D 11011 0001A 1010F 1111


2.5.47 将十六进制补码转换为十进制数
a. xF0-1111 0000,其十进制数为1001 0000:-16
b. x7ff-02047111 1111 1111 ,其十进制数为2047
c. x16-0001 0110,其十进制数为16+6=22
d. x8000-1000 0000 0000 0000,其十进制数为-32768

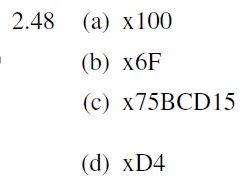

十六进制加法,逢16进1,
a. B+E=9+16,5+D+1=3+16,6+2+1=9,结果为X2939,最高bit没有发生变号,未发生溢出
b. 6+0=6,9+A=3+16,D+0+1=E,7+F=6,由于是异号相加,所以一定不发生溢出,结果为X6E36
c. D+7=4+16,9+5+1=F,3+3=6,A+A=4+16,同号相加,符号位变号,发生溢出
d. 6+2=8,9+1=A,D+4=1+16,7+7+1=F,同号相加,符号位变号,发生溢出

逻辑运算是按位运算,必须展开为二进制

转二进制,再转16进制
a. 25675=16384+8192+1024+64+8+2+1
0110 ⏟ 6 0100 ⏟ 4 0100 ⏟ 4 1011 ⏟ B \underbrace{0110}_{6} \underbrace{0100}_4 \underbrace{0100}_4 \underbrace{1011}_B 6 01104 01004 0100B 1011
b. 675.625=512+128+32+2+1+0.5+0.125
1010100011.101 = 1.010100011101 × 2 9 = 1.010100011101 × 2 1001 10 1010 0011.101=1.010100011101\times 2^{9}=1.010100011101\times 2^{1001} 1010100011.101=1.010100011101×29=1.010100011101×21001
表示为IEEE754格式,数符0,阶码9+127=128+8=1000 1000,尾数 010100011101 00 ⋯ 0 ⏟ 9 010100011101\underbrace{00\cdots0}_{9} 0101000111019 00⋯0
0100 0100 0010 1000 1110 1000 0000 0000,其十六进制为X4428E800
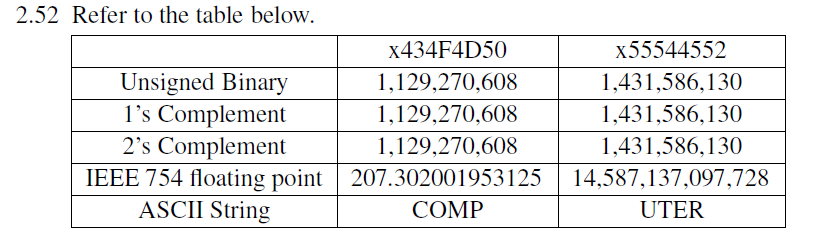
2.5.53
Q 1 = ! ( A ∗ B ) = A ‾ + B ‾ Q_1=!(A*B)=\overline{A}+\overline{B} Q1=!(A∗B)=A+B
Q 2 = ! ( ! A ∗ ! B ) = A + B Q_2=!(!A * !B)=A+B Q2=!(!A∗!B)=A+B
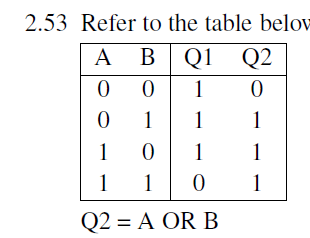
2.5.54
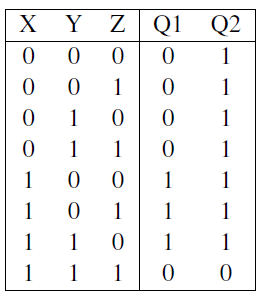
Q 1 = ! ( ! X + ( X Y Z ) ) = X ( X ‾ + Y ‾ + Z ‾ ) = X Y ‾ + X Z ‾ Q_1=!(!X+(XYZ))=X(\overline{X}+\overline{Y}+\overline{Z})=X\overline{Y}+X\overline{Z} Q1=!(!X+(XYZ))=X(X+Y+Z)=XY+XZ
Q 2 = ( Y + Z ) X Y Z ‾ = Y ‾ Z ‾ + X ‾ + Y ‾ + Z ‾ = X ‾ + Y ‾ + Z ‾ Q_2=\overline{(Y+Z)XYZ}=\overline{Y}\overline{Z}+\overline{X}+\overline{Y}+\overline{Z}=\overline{X}+\overline{Y}+\overline{Z} Q2=(Y+Z)XYZ=YZ+X+Y+Z=X+Y+Z


c. 023+221:3+1=0+4,2+2+1=1+4,0+2+1=3,所以310
d. 42/4=10(2),10/4=2(2),2/4=2,所以222
e. 123.3 = 3 + 2 ∗ 4 + 1 ∗ 16 + 3 4 = 27.75 = 11011.11 123.3=3+2*4+1*16+\frac{3}{4}=27.75=11011.11 123.3=3+2∗4+1∗16+43=27.75=11011.11

1110 0101
数符1 负数
阶码1100,指数12-7=5
尾数1.101,小数1.101
− 1.101 × 2 5 = − 110100 = − 52 -1.101\times 2^{5}=-110100=-52 −1.101×25=−110100=−52