1 前言

很久之前记录了一篇博客PCL点云配准_thequitesunshine007的博客-CSDN博客

 ，记录的是基于点特征（FPFH特征描述子）匹配的SAC-ICP点云配准思想。

今天记录一下完全不一样的点云配准方法NDT。

2 介绍

2.1 多元正态分布

 如果随机变量X满足正态分布（即 X∼N(μ,σ) ）,则其概率密度函数为：

其中的 μ 为正态分布的均值， σ2 为方差，这是对于维度 D=1 的情况而言的。
对于多元正态分布而言，其概率密度函数可以表示为：

 

其中u 表示均值向量，而∑表示协方差矩阵。协方差矩阵对角元素表示的是对应的元素的方差，非对角元素则表示对应的两个元素（行与列）的相关性。协方差矩阵对角元素表示的是对应的元素的方差，非对角元素则表示对应的两个元素（行与列）的相关性。

 

2.2  NDT算法介绍

       NDT正态分布点云算法，即Normal Distribution Transform，是将参考点云转换成多维变量的正态分布来进行配准。如果变换参数能够使得两幅激光数据匹配得很好，那么变换点在参考点云中对应的概率密度将会很大。因此，要使得两幅激光点云数据匹配最优，只需用优化方法迭代计算使得概率密度之和最大的转换矩阵。

       现实中，LiDAR扫描得到的点云可能和参考点云（如高精地图点云）存在细微的区别，此偏差可能来自于测量误差，也有可能是“场景”发生了一下变化（比如说行人，车辆）。NDT配准可以忽略细微变化，因此可用于解决这些细微的偏差问题。同时，NDT相对与ICP，它耗时稳定，跟初值相关不大，初值误差大时，也能很好得纠正过来。计算正态分布是个一次性的工作，因为其在配准中不利用对应点的特征计算和匹配，不需要消耗大量代价计算最邻近点，所以时间较快。

2.3 算法流程

1. 将空间（reference scan）划分成各个格子cell（也叫体素voxel grid）；
2. 将参考点云投（映射）到各个网格中；
3. 基于网格中的点，计算格子的正态分布概率密度函数（probability density function, PDF）的参数；

 其中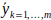，表示这个网格内所有的扫描点的位置，表示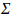网格内点的协方差；

 4. 将第二幅点云的每个点按转换矩阵变换；
 5. 第二幅扫描点云的点落于参考点云的哪个网格，计算相应的概率分布函数PDF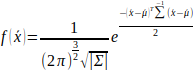

 6. 求最大似然函数，得到最优变换参数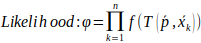

当前扫描为一个点云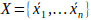，给定扫描点集合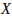和变换参数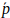，令空间转换函数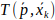表示使用姿态变换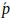来移动点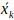，并求出转换后的点的PDF，那么能够使似然函数最大化的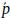，就是最优的变换参数。

 最大化似然相当于最小化负对数似然函数：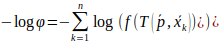

然后使用优化算法来调整参数，以最小化负对数似然函数。NDT算法使用牛顿法进行参数优化。

 2.4 NDT算法可视化理解

下图形象得表示了正太分布算法将点云参考空间分为很多网格，并根据网格中点的分布，计算每个网格的PDF：

 使用正态分布来表示原本离散的点云有诸多好处，这种分块的（通过一个个cell）光滑的表示是连续可导的，每一个概率密度函数可以被认为是一个局部表面（local surface）的近似,它不但描述了这个表面在空间中的位置，同时还包含了这个表面的方向和光滑性等信息。下图是一个3D点云及其网格化效果:

 上图中立方体的边长为 1 米，其中越明亮的位置表示概率越高。此外，局部表面的方向和光滑性则可以通过协方差矩阵 的特征值和特征向量反映出来。我们以三维的概率密度函数为例，如果三个特征值很接近，那么这个正态分布描述的表面是一个球面；如果一个特征值远大于另外两个特征值，则这个正态分布描述的是一条线；如果一个特征值远小于另外两个特征值，则这个正态分布描述的是一个平面。下图描述了协方差矩阵特征值和表面形状之间的关系：

 

 

3 NDT算法PCL实现

PCL库中已有NDT算法实现，用NDT算法求出两个多于100,000个点的点云之间的刚体变换：
http://pointclouds.org/documentation/tutorials/normal_distributions_transform.php

对于NDT算法的内部原理，可以参见Dr. Martin Magnusson的博士论文“The Three-Dimensional Normal Distributions Transform – an Efficient Representation for Registration, Surface Analysis, and Loop Detection”。

参考：

NDT点云配准算法_ndt配准_海清河宴的博客-CSDN博客