1.3.1背包模型（一）

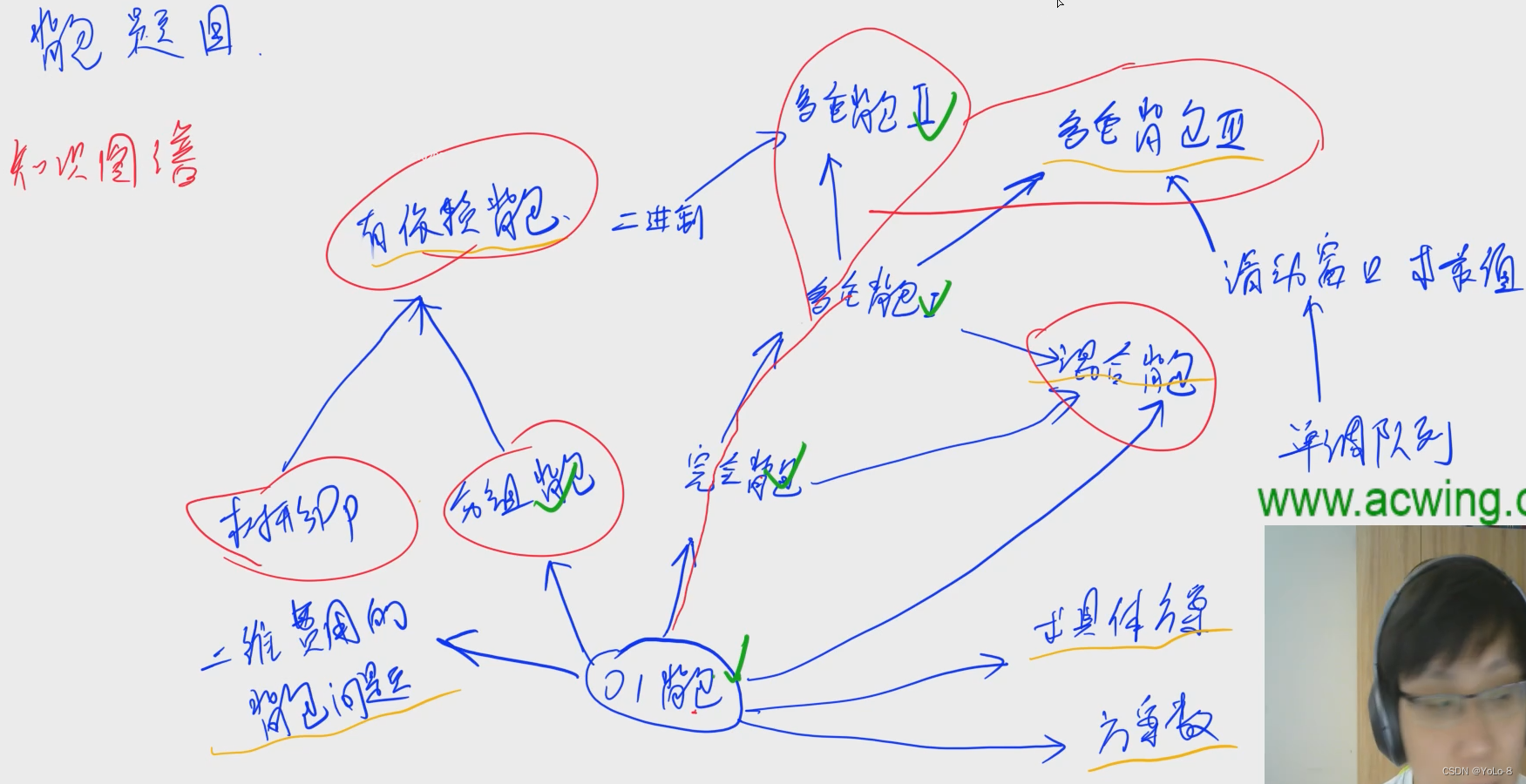
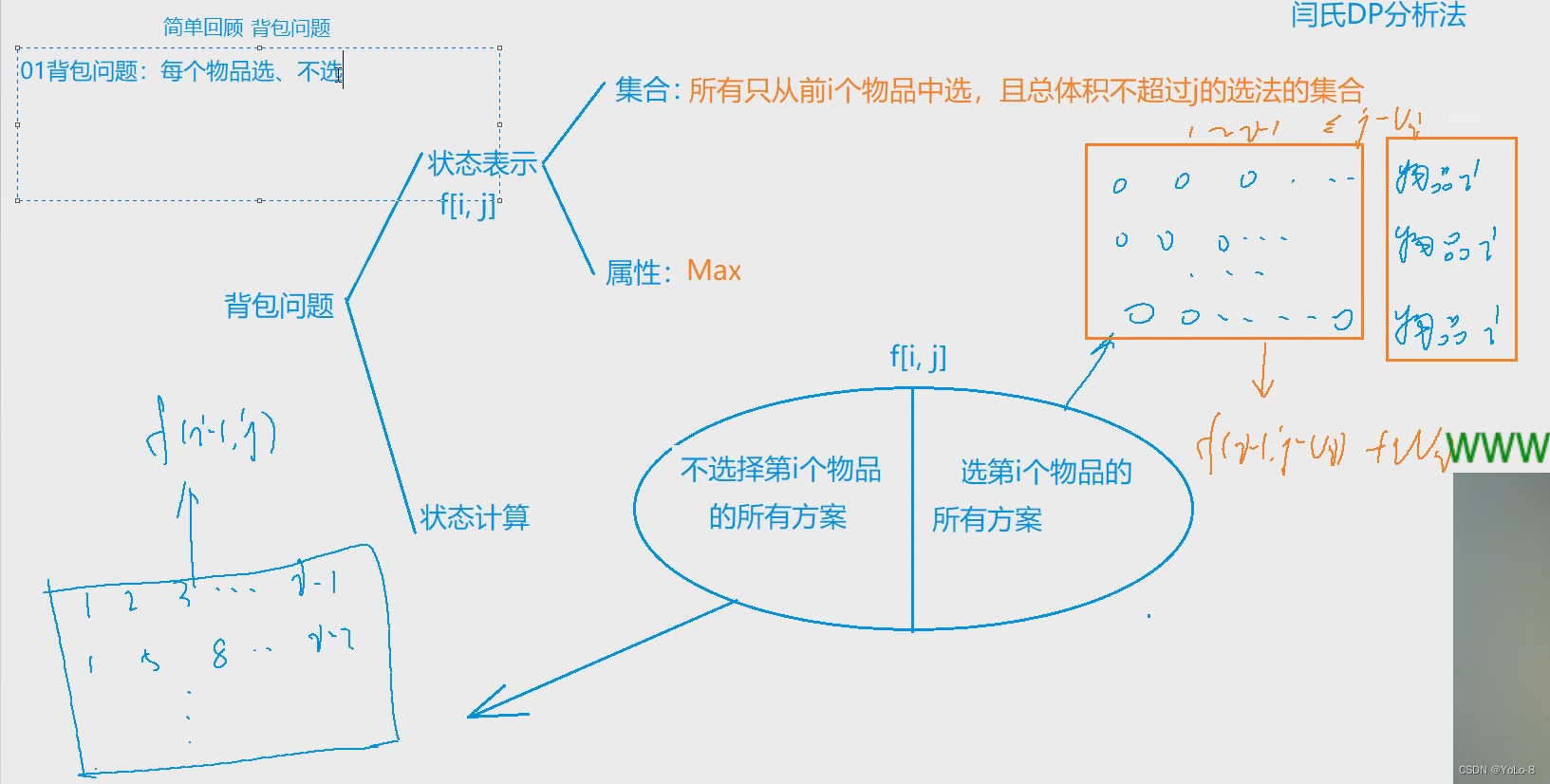
在这里插入图片描述

01背包
划分依据：依靠“最后一步”来划分
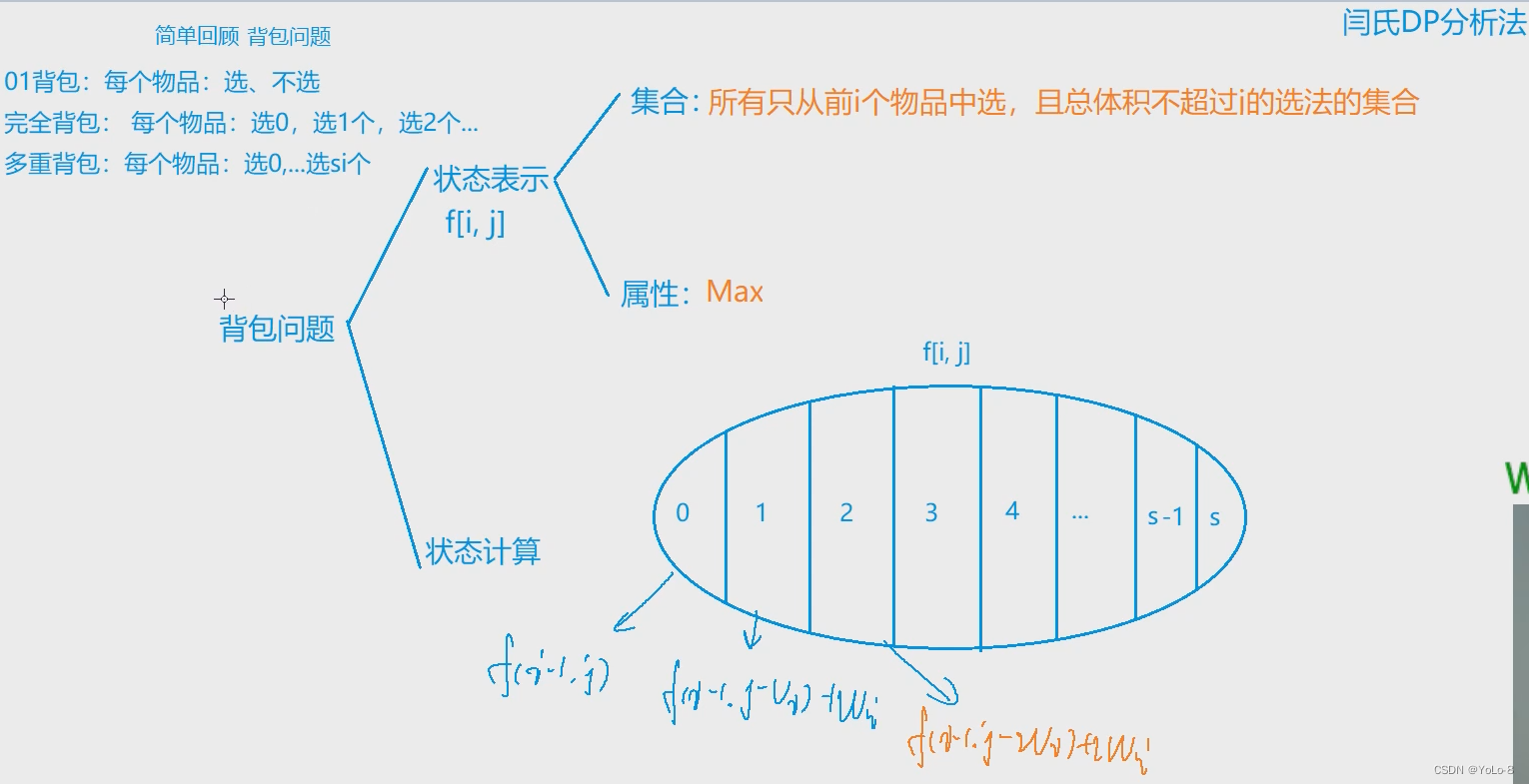
在这里插入图片描述
完全背包

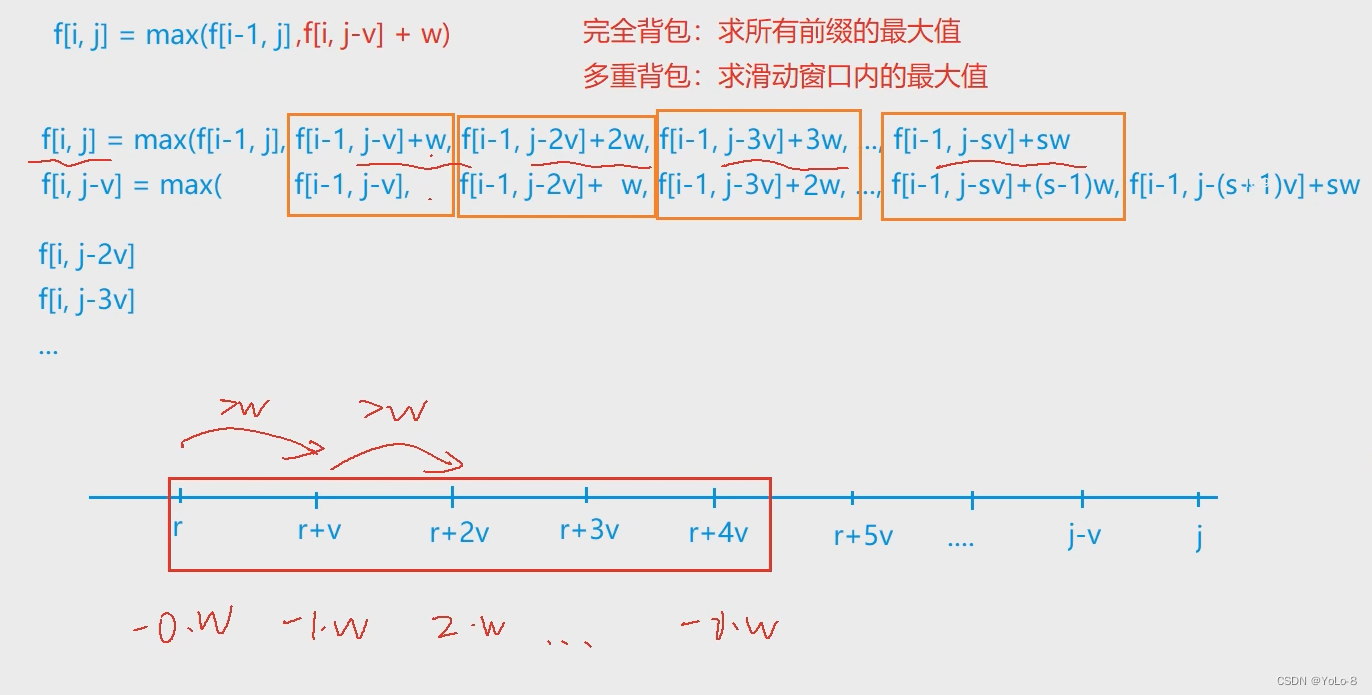
在这里插入图片描述

多重背包
在这里插入图片描述

完全背包：求所有前缀的最大值
多重背包：求滑动窗口内的最大值

1.多重背包问题 III

有 $N$ 种物品和一个容量是 $V$ 的背包。

第 $i$ 种物品最多有 $s_{i}$ 件，每件体积是 $v_{i}$ ，价值是 $w_{i}$ 。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数， $N ， V (0 < N \leq 1000, 0 < V \leq 20000)$ ，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_{i}$ , $w_{i}$ , $s_{i}$ 用空格隔开，分别表示第 i种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
$0 < N \leq 1000$
$0 < V \leq 20000$
$0<v_{i},w_{i},s_{i}≤20000$

提示
本题考查多重背包的单调队列优化方法。

输入样例

输出样例：

1.1题解

难度警告！本题为楼教主男人八题之一，量力而行！
题目大意：
本题为多重背包问题
解题方法：
我们先分析一下式子吧。
在这里插入图片描述
好了，我来解释一下这些式子
$r$ ：就是 $j$ 一直减去 $v$ 最后剩下的余数。

然后我们会发现这回不能用之前的式子推了，因为 $f [i] [j - v]$ 后面多出了一项。我们知道最后一项的值，但是却不能因此推出前面这几项的值。
数学老师经常跟我们说：遇事不决就画图。那我就画一个试一试。
在这里插入图片描述
我只是示意一下，这个图底下标的就是体积
我们会发现，每个 $f$ 数组里的数，转移的都是一个长度为 $k + 1$ 的区间！
在图中就是这样体现的：

$f [i] [j]$ 不就是从 $f [i - 1] [j] ， f [i - 1] [j - v] + w ， f [i - 1] [j - 2 v] + 2 w ...... f [i - 1] [j - s v] + s w$
转移过来的，就是一个长度为 s+1的窗口！

~~好了这道题你就已经做了一半了，喝口水休息一下吧~~~

接下来继续往下看。
我们会发现，一开始的式子，对应到这个数轴上，就是越往左边加的 $w$ 越大，所以我们需要体现出越往左加的 $w$ 越多的这个优势，所以式子变成了这样：

在这里插入图片描述
也就是每个对应上减去一些 $w$

在这里插入图片描述
问题环节：
我Q：为什么要这么做呢？你是不是闲的蛋疼？？？
我A：具体就是 当前下标 和该 最大值的下标 之间差了 $x$ 个 $v$ ，那么就要加上 $x$ 个 $w$ 。重点就是比较的时候是比较相对大小而不是绝对大小！！！讲细一点就是说你无法确定单调队列里的数到底加上了几个 $w$ ，就无法比较了。
我Q: 懂了懂了nbnb点赞点赞。

1.2代码实现

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 20010;
int n, m;
int f[N], g[N], q[N];
//拷贝数组，因为这里不能使用一维优化，因为如果倒叙枚举，你就不能用滑动窗口了。

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);
        for (int j = 0; j < v; j ++ ) {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v) {
                if (hh <= tt && q[hh] < k - s * v) hh ++ ; //剔除超出长度元素
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w); //更新当前答案
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt -- ;
                //维持单调性
                //这里也可以这样写，更易理解
                //while (hh <= tt && g[q[tt]] <= g[k] - (k - q[tt]) / v * w) tt -- ;
                q[ ++ tt] = k;
            } 
        }
    }
    cout << f[m] << endl;
    return 0;
}

2.采药

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。

为此，他想拜附近最有威望的医师为师。

医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式
输入文件的第一行有两个整数 $T$ 和 $M$ ，用一个空格隔开， $T$ 代表总共能够用来采药的时间， $M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间（包括 $1$ 和 $100$ ）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式
输出文件包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

数据范围
$1 \leq T \leq 1000$ ,
$1 \leq M \leq 100$
输入样例：

输出样例：

2.1题解

参考01背包

2.2代码

#include<iostream>

using namespace std;

const int N = 1010;

int n,m;
int f[N];

int main()
{
    cin>>m>>n;
    for(int i = 0; i < n;i++)
    {
        int v,w;
        cin>>v>>w;
        for(int j = m;j >= v;j--)   f[j] = max(f[j],f[j - v] + w);
    }
    
    cout<<f[m]<<endl;
    
    return 0;
}

3.装箱问题

有一个箱子容量为 $V$ ，同时有 $n$ 个物品，每个物品有一个体积（正整数）。

要求 $n$ 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入格式
第一行是一个整数 $V$ ，表示箱子容量。

第二行是一个整数 $n$ ，表示物品数。

接下来 $n$ 行，每行一个正整数（不超过 $10000$ ），分别表示这 $n$ 个物品的各自体积。

输出格式
一个整数，表示箱子剩余空间。

数据范围
$0 < V \leq 20000$ ,
$0 < n \leq 30$
输入样例：

输出样例：

3.1题解

此题为01背包变形题目，注意，此题需要将体积看为价值即可。

3.2代码实现

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 20010;

int m,n;
int f[N];
int main()
{
    cin>>m>>n;
    for(int i = 0;i < n;i++)
    {
        int v;
        cin>>v;
        //m表示容量
        for(int j = m;j >= v;j--) f[j] = max(f[j],f[j - v] + v);

    }
    //注意：剩余空间
    cout<<m - f[m]<<endl;
    
    return 0;
}

4宠物小精灵之收服

宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。

一天，小智和皮卡丘来到了小精灵狩猎场，里面有很多珍贵的野生宠物小精灵。

小智也想收服其中的一些小精灵。

然而，野生的小精灵并不那么容易被收服。

对于每一个野生小精灵而言，小智可能需要使用很多个精灵球才能收服它，而在收服过程中，野生小精灵也会对皮卡丘造成一定的伤害（从而减少皮卡丘的体力）。

当皮卡丘的体力小于等于0时，小智就必须结束狩猎（因为他需要给皮卡丘疗伤），而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。

当小智的精灵球用完时，狩猎也宣告结束。

我们假设小智遇到野生小精灵时有两个选择：收服它，或者离开它。

如果小智选择了收服，那么一定会扔出能够收服该小精灵的精灵球，而皮卡丘也一定会受到相应的伤害；如果选择离开它，那么小智不会损失精灵球，皮卡丘也不会损失体力。

小智的目标有两个：主要目标是收服尽可能多的野生小精灵；如果可以收服的小精灵数量一样，小智希望皮卡丘受到的伤害越小（剩余体力越大），因为他们还要继续冒险。

现在已知小智的精灵球数量和皮卡丘的初始体力，已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。

请问，小智该如何选择收服哪些小精灵以达到他的目标呢？

输入格式

输入数据的第一行包含三个整数： $N ， M ， K$ ，分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。

之后的K行，每一行代表一个野生小精灵，包括两个整数：收服该小精灵需要的精灵球的数量，以及收服过程中对皮卡丘造成的伤害。

输出格式

输出为一行，包含两个整数： $C ， R$ ，分别表示最多收服 $C$ 个小精灵，以及收服 $C$ 个小精灵时皮卡丘的剩余体力值最多为R。

数据范围
$0 < N \leq 1000$ ,
$0 < M \leq 500$ ,
$0 < K \leq 100$

输入样例1：

输出样例1：

3 30

输入样例2：

输出样例2：

0 100

4.1题解

二维费用01背包问题
在这里插入图片描述

注意：题目说道：使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服，因此皮卡丘的体力值需在V2 - 1时开始

4.2代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 510;

int n, V1, V2;
int f[N][M];

int main()
{
    cin >> V1 >> V2 >> n;
    for (int i = 0; i < n; i ++ )
    {
        int v1, v2;
        cin >> v1 >> v2;
        for (int j = V1; j >= v1; j -- )
            for (int k = V2 - 1; k >= v2; k -- )
                f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
    }

    cout << f[V1][V2 - 1] << ' ';
    int k = V2 - 1;//找到当前皮卡丘消耗体力最少的情况
    while (k > 0 && f[V1][k - 1] == f[V1][V2 - 1]) k -- ;
    cout << V2 - k << endl;

    return 0;
}