智能优化算法一元函数优化

news2024/11/26 20:47:46

目录

一、问题描述

二、解决方法

1.模拟退火

1.1 算法思路

1.2 求解代码

1.3 计算结果

2.粒子群算法 

2.1 算法思路

2.2 求解代码 

2.3 计算结果 

3.遗传算法

3.1 算法思路

3.2 求解代码

3.3 计算结果

一、问题描述

本篇文章所做的是分别用模拟退火、粒子群算法、遗传算法求解一元函数

                                 10*sin(5*x)+7*\left | x-5 \right |+10

这一函数在0-10区间的最大值问题，其函数图像为：

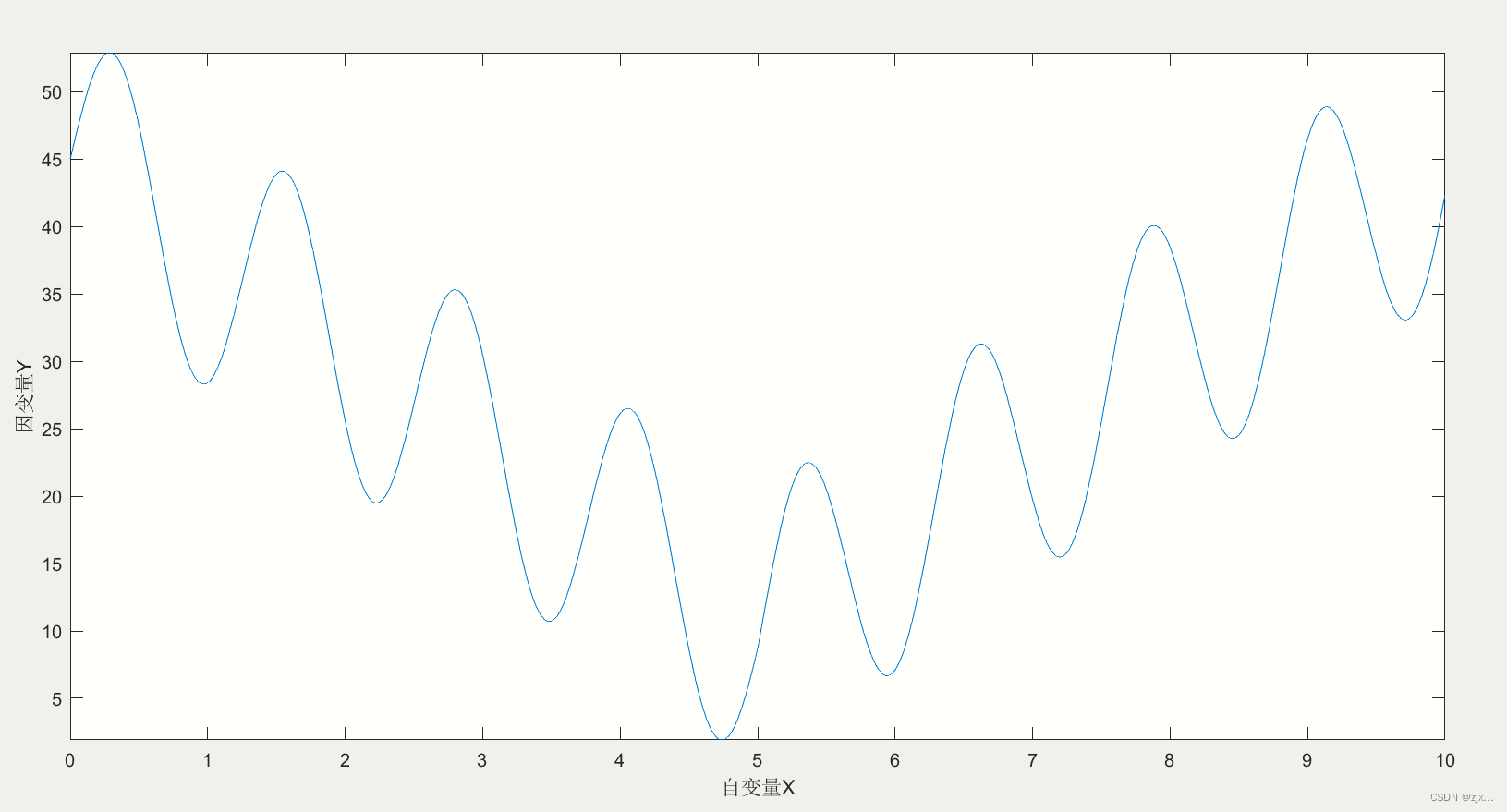
二、解决方法

1.模拟退火

1.1 算法思路

  1. 首先，定义目标函数 f，该函数以一个变量 x 为输入，并返回一个数值。然后使用 fplot 函数绘制了这个函数在取值范围（即 0 - 10）之间的图像。
  2. 接着，定义了初始温度 T，结束温度 T_final，以及降温系数 alpha。
  3. 设定了自变量的取值范围 xlimit，在取值范围内随机选择一个值来定义初始解 init_x。
  4. 定义了最大迭代次数 max_iterations。
  5. 初始化了最优解 best_x 和最优解的函数值 best_f，它们的初始值设为初始解及其函数值。
  6. 开始模拟退火算法的主要循环，迭代次数从1到最大迭代次数。
  7. 在每次迭代中，在初始解上添加一个随机噪声得到一个新的解 new_x，并将其将新解限制在取值范围内。
  8. 计算新解与当前解的函数值的差值 delta_f。
  9. 如果新解的函数值比当前最优解的函数值更好（即 delta_f 大于0），或者满足Metropolis准则（即以一定的概率接受比当前最优解更差的解），那么接受新解作为当前解。
  10. 如果新解比当前最优解更好，更新最优解。
  11. 每次迭代后降低温度，如果温度已经低于结束温度，结束算法，否则继续迭代。

1.2 求解代码

function SA()

% 定义目标函数,并展示图像
f = @(x)10.*sin(5.*x)+7.*abs(x-5)+10;
figure(1);
fplot(f,[0,10]);
hold on
xlabel('自变量X');
ylabel('因变量Y');
  

% 定义初始温度和结束温度与降温系数 
T = 1000;  
T_final = 1e-6;  
alpha = 0.99;  

% 定义取值范围
xlimit = [0,10];
  
% 定义初始温度下的初始解  
init_x = xlimit(1, 1) + (xlimit(1, 2) - xlimit(1, 1)) * rand();
  
% 定义最大迭代次数  
max_iterations = 10000;  
  
% 初始化最优解和最优解的函数值  
best_x = init_x;  
best_f = f(init_x);  
  
% 开始模拟退火算法  
for iter = 1:max_iterations  
    % 生成新解  
    new_x = init_x + randn; 
    
    % 控制解的范围在给定区间内
    new_x = max(min(new_x, xlimit(2)), xlimit(1));
      
    % 计算目标函数值的差值  
    delta_f = f(new_x) - f(init_x);  
      
    % 如果新解更好，或者满足Metropolis准则，则接受新解  
    if delta_f > 0 || exp(-delta_f/T) > rand()  
        init_x = new_x;  
        if f(new_x) > best_f  
            best_x = new_x;  
            best_f = f(new_x);  
        end  
    end  

    % 展示当前最优解的情况
    plot(best_x,best_f,'b*','MarkerSize',5);
    title(strcat('当前迭代次数：',num2str(iter)));
    pause(0.03);
      
    % 降温  
    T = T* alpha^(iter/100);  
      
    % 如果温度足够低，结束算法  
    if T < T_final  
        break;  
    end  
end  
  
% 展示最终的结果
plot(best_x,best_f,'r*','MarkerSize',10);
grid on;
hold off;
fprintf(['The best x is --->\t',num2str(best_x),'\nThe fitness value is --->\t',num2str(best_f),'\n'])

end

1.3 计算结果

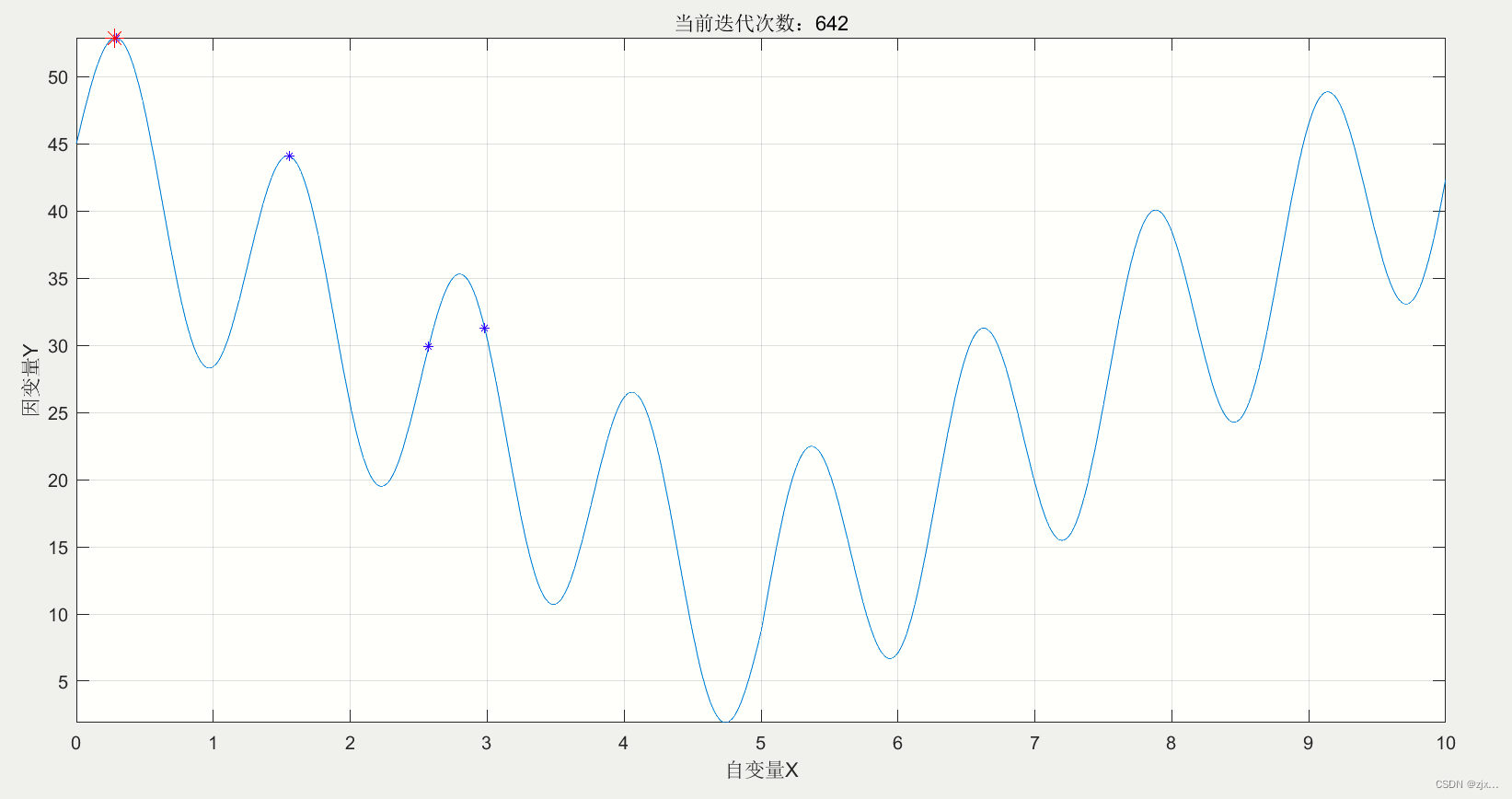
The best x is --->    0.28093
The fitness value is --->    52.8958 

2.粒子群算法 

2.1 算法思路

  1. 首先定义了种群个数、迭代次数、惯性权重、可信度因子以及允许的精度误差。
  2. 然后定义位置与速度的限制范围。
  3. 接着，初始化了种群位置（x）、种群进化速度（v）、个体历史最佳位置（individual_best_x）、个体历史最佳适应度（individual_best_fitness）、种群历史最佳位置（global_best_x）、种群历史最佳适应度（global_best_fintness）等参数。
  4. 进行粒子群算法的优化迭代。
  5. 记录当前的种群历史最佳适应度（old_global_best_x）。
  6. 然后计算每个粒子的适应度存储到 fitness 中。
  7. 更新个体最佳适应度与位置、种群最佳适应度与位置。
  8. 更新速度，公式为：

                               v = v + c1 * rand() * (pBest - present) + c2 * rand() * (gBest - present)

    其中

      v：粒子的速度向量                                          pBest：粒子自身历史最优位置

      present：当前粒子的位置向量                        gBest：全局最优位置

      c1 和 c2：学习因子                                   rand()：[0, 1)之间的随机数  

  9. 限定速度范围，更新位置，限定位置范围。
  10. 判断迭代的历史最佳适应度和位置不会有太大的精度变化，若变化小于精度值则停止迭代。

2.2 求解代码 

function PSO()

N = 50;   % 初始种群个数
iterations = 200;  % 迭代的次数
w = 0.8;  % 惯性权重
c1 = 0.5; % 可信度因子1
c2 = 0.5; % 可信度因子2
precision = 0.001;   % 允许的精度误差

% 展示函数图像
figure(1);
fplot(@(x)10.*sin(5.*x)+7.*abs(x-5)+10,[0,10]);
hold on
xlabel('自变量X');
ylabel('因变量Y');

xlimit = [0,10];  % 设置位置参数限制
vlimit = [-1,1];  % 设置速度限制

% 初始化种群位置
x = xlimit(1, 1) + (xlimit(1, 2) - xlimit(1, 1)) * rand(1,N);  
% 初始化种群速度
v = rand(1,N);
% 每个个体的历史最佳位置初始化
individual_best_x = x;
% 每个个体的历史最佳适应度初始化
individual_best_fitness = zeros(1,N);
for i = 1:N
    individual_best_fitness(i) = objective_function(x(i));    
end
% 种群的最佳历史位置初始化
global_best_x = 0 ;
% 种群最佳历史适应度初始化
global_best_fintness = -inf;


iter = 1;
while iter <= iterations
    % 将历史最佳位置进行copy
    old_global_best_x = global_best_x;  

    % 计算每个粒子适应度,并记录在 fitness 中
    fitness = zeros(1,N);
    for i = 1:N
        fitness(i) = objective_function(x(i));
    end

    % 遍历每个粒子，如果该粒子的当前适应度大于其历史最佳适应度，则将该粒子的当前适应度作为历史最佳适应度，并将历史最佳位置赋值为当前位置。
    for i = 1:N
        if individual_best_fitness(i) < fitness(i)
            individual_best_fitness(i) = fitness(i);
            individual_best_x(i) = x(i);
        end
    end

    % 如果所有粒子中的最大适应度已经大于了全局历史最佳适应度，则将最大适应度最为全局历史最佳适应度，并记录位置
    if global_best_fintness < max(individual_best_fitness)
        [global_best_fintness, idx] = max(individual_best_fitness); % idx 为最佳适应度的位置标号
        global_best_x = individual_best_x(idx);
    end


    % 更新速度
    v = v .* w + c1 .* rand(1,N) .* (individual_best_x - x) + c2 .* rand(1,N) .* (repmat(global_best_x, 1, N) - x);

    % 将速度调整在限定范围内
    for i =1:size(v,2)
        v(i) = max(min(v(i), vlimit(2)), vlimit(1));
    end

    % 更新位置
    x = x + v;
    
    % 将位置调整在限定范围内
    for i =1:size(x,2)
        x(i) = max(min(x(i), xlimit(2)), xlimit(1));
    end

    % 如果迭代的历史最佳适应度和位置不会有太大的精度变化就停止
    if iter > 100
        if abs(global_best_x - old_global_best_x) < precision
            break
        end
    end

    % 展示每一次迭代中的最优解
    plot(global_best_x,global_best_fintness,'b*','MarkerSize',5);
    title(strcat('当前迭代次数：',num2str(iter)));
    pause(0.03);

    iter = iter + 1;
end

% 展示最终的结果
plot(global_best_x,global_best_fintness,'r*','MarkerSize',10);
grid on;
hold off;
fprintf(['The best x is --->\t',num2str(global_best_x),'\nThe fitness value is --->',num2str(global_best_fintness),'\n'])

end

% 定义目标函数
function fitness=objective_function(decimal_value)
    fitness=10*sin(5*decimal_value)+7*abs(decimal_value-5)+10;
end

2.3 计算结果 

The best x is --->    0.28607
The fitness value is --->52.899 

3.遗传算法

3.1 算法思路

  1. 初始化种群、染色体、交叉率、变异率、迭代次数等一系列参数
  2. 遗传算法循环迭代
  3. 将二进制编码转化为十进制数值，即将二进制字符串转化为实际的自变量值。
  4. 计算每个个体的适应度，即通过目标函数对应的数学计算，求得每个个体适应度值。
  5. 选择操作，根据适应度值进行轮盘赌选择，选择出新的种群。
  6. 交叉操作，采用单点交叉的方式对新种群进行交叉，生成新的子代个体。
  7. 变异操作，以一定的概率对新种群进行变异，引入新的个体差异性。
  8. 更新种群，计算新种群的适应度，记录最佳适应个体和适应度值，并绘制当前最佳个体的散点图。
  9. 重复以上步骤，直到达到最大迭代次数。

3.2 求解代码

function GA()

figure(1);
fplot(@(x)10.*sin(5.*x)+7.*abs(x-5)+10,[0,10]);
hold on
xlabel('自变量X');
ylabel('因变量Y');

population_size=20;     % 种群大小
chromosome_length=20;   % 染色体长度
crossover_possibility=0.7;        % 交叉率
mutation_possibility=0.1;         % 变异率
max_generations=200;           % 最大迭代次数
bestfitness=-inf;       % 最佳适应度
bestindividual=0;       % 最佳适应个体
result=zeros(2,max_generations);       % 每次迭代的最佳适应个体与适应度
xlimit=[0,10];


% 初始化种群
population=round(rand(population_size,chromosome_length));     % 生成 population_size 个长度为 chromosome_length 字符串


% 循环迭代
for iter=1:max_generations
    
    % 1.二进制转化为十进制
    decimal_value = transcoding(population,xlimit,chromosome_length);
    

    % 2.计算函数目标值
    fitvalue=objective_function(decimal_value);


    % 3.选择操作（轮盘赌法）
    new_population=select(population,fitvalue);


    % 4.交叉操作（单点交叉）
    new_population = crossover(new_population,crossover_possibility);


    % 5.变异操作
    new_population = mutation(new_population,mutation_possibility);
    

    % 更新种群，重新计算种群的适应度，记录Best
    population=new_population;
    decimal_value = transcoding(population,xlimit,chromosome_length);
    fitvalue=objective_function(decimal_value);

    [row,~]=size(population);
    for i=1:row
        if bestfitness<fitvalue(i)
            bestfitness=fitvalue(i);
            bestindividual=decimal_value(i);
        end
    end
    result(1,iter)=bestindividual;
    result(2,iter)=bestfitness;
    plot(result(1,iter),result(2,iter),'b*','MarkerSize',5);
    title(strcat('当前迭代次数：',num2str(iter)));
    pause(0.03);
end
plot(result(1,end),result(2,end),'r*','MarkerSize',10);
grid on;
hold off;
fprintf(['The best x is --->\t',num2str(bestindividual),'\nThe fitness value is --->',num2str(bestfitness),'\n'])
end

% 定义目标函数
function fitness=objective_function(decimal_value)
    fitness=10*sin(5*decimal_value)+7*abs(decimal_value-5)+10;
end


% 选择
function new_population=select(population,fitvalue)
    [row,col]=size(population);
    new_population=zeros(row,col);
    fitvalue_possibility=fitvalue/sum(fitvalue);  % 适应度与所有适应度的之和的比
    fitvalue_possibility=cumsum(fitvalue_possibility);  % 离散的概率转为0-1区间的累计和

    p_rand = sort(rand(row,1));  % 一列由小到大排列的随机数
    % 用p_rand去与做完了累计和的p_fitvalue作比较
    % 适应度越高就有越大的机率在p_fitvalue的累计和中占据更大的区间
    % 将会有较多的p_rand值落在区间
    % 用这种方法保留了适应度较大的基因
    i=1;
    j=1;
    while i <= row
        if p_rand(i)<fitvalue_possibility(j)
            new_population(i,:)=population(j,:);
            i=i+1;
        else
            j=j+1;
        end
    end
end


% 交叉
function new_population=crossover(population,crossover_possibility)
    [row,col]=size(population);
    new_population=zeros(row,col);
    for i=1:2:row-1  % 让i与i+1进行交叉，所以i遍历染色体中的编号为奇数就可以
        if rand<crossover_possibility
            point=round(rand*col);   % 在py位二进制中随机选一个交叉点位
            new_population(i,:)=[population(i,1:point),population(i+1,point+1:end)];
            new_population(i+1,:)=[population(i+1,1:point),population(i,point+1:end)];
        else
            % 有一定几率不发生交叉
            new_population(i,:)=population(i,:);
            new_population(i+1,:)=population(i+1,:);
        end
    end
end


% 变异
function new_population=mutation(population,mutation_possibility)
    [row,col]=size(population);
    new_population=zeros(row,col);
    for i=1:row
        if rand<mutation_possibility  % 发生变异
            mutation_point=round(rand*col);  % 发生变异时的位点
            if mutation_point<=0
                mutation_point=1;   % 检测越界
            end
            new_population(i,:)=population(i,:);  % 变异后的种群存储在newpop3中
            if new_population(i,mutation_point)==0 % 将变异点位上的二进制数取反
                new_population(i,mutation_point)=1;
            else
                new_population(i,mutation_point)=0;
            end
        else    % 没有发生变异
            new_population(i,:)=population(i,:);
        end
    end
end


% 编码转换
function decimal_value = transcoding(population,xlimit,chromosome_length)
    [row,col]=size(population);  % 种群的行列数
    convert=zeros(row,col);
    for j=1 : col
        convert(:,j)=population(:,j)*2^(col-j);     % 将二进制对应为 1 的部分赋值为相应的数值
    end
    temp=sum(convert,2);        % 将这些数值加起来转换为10进制
    decimal_value=xlimit(1)+temp*((xlimit(2)-xlimit(1))/2^chromosome_length);       % 将这些数据转化为定义的上下区间内的值
end

3.3 计算结果

 

The best x is --->    0.2987
The fitness value is --->52.8792

        

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/940823.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL 8.1安装

MySQL 8.1安装

1. 下载地址 https://dev.mysql.com/downloads/mysql/8.0.html 我这里没有采用installer安装&#xff0c;因为installer安装依赖visual studio&#xff0c;所以&#xff0c;我下载的是zip文件。 最终下载的版本如下&#xff1a; 2. 添加环境变量 解压&#xff0c;添加环境…
阅读更多...
图的存储：邻接表法

图的存储：邻接表法

1.邻接表的定义 不同于邻接矩阵&#xff08;二维数组存储&#xff09;&#xff0c;邻接表采用的顺序链式存储实现的。 1.存储方式 顶点&#xff1a;使用结构体存储顶点&#xff0c;一个顶点包括顶点信息和指向第一条边或者弧的指针。用邻接表存储图&#xff1a;使用结构体存…
阅读更多...
Spring Boot存在路径遍历漏洞CVE-2021-22118

Spring Boot存在路径遍历漏洞CVE-2021-22118

文章目录 0.前言1.参考文档2.基础介绍1. 影响的版本2. **漏洞利用原理&#xff1a;** 3.解决方案3.1. 方案13.2. 方案23. 方案3 0.前言 背景&#xff1a;Spring Boot存在路径遍历漏洞。CVE-2021-22118: 官方 issue也有对此的记录&#xff0c;感兴趣可以看下 https://github.com…
阅读更多...
Spring Boot集成MyBatis Plus

Spring Boot集成MyBatis Plus

文章目录 一、前言二、步骤2.1、步骤 1&#xff1a;创建 Spring Boot 项目2.2、添加依赖2.2.1、基本的Spring和Spring MVC功能2.2.2、MySQL驱动依赖2.2.3、 MyBatis Plus 的依赖 2.3、配置数据库连接2.4、创建实体类2.5、创建 Mapper 接口2.6、编写 Service 层2.7、编写 Contro…
阅读更多...
自动化运维工具——ansible安装及模块介绍

自动化运维工具——ansible安装及模块介绍

目录 一、ansible——自动化运维工具 1.1 Ansible 自动运维工具特点 1.2 Ansible 运维工具原理 二、安装ansible 三、ansible命令模块 3.1 command模块 3.2 shell模块 3.3 cron模块 3.4 user模块 3.5 group 模块 3.6 copy模块 3.7 file模块 3.8 ping模…
阅读更多...
Mat类数据的读取

Mat类数据的读取

目录 1.Mat类矩阵的常用属性 2.Mat元素的读取 1.at方法读取Mat矩阵元素 at (int row,int col) 2.矩阵元素地址定位方式访问元素 3.Android jni demo 1.Mat类矩阵的常用属性 下面是一些Mat类的常用属性&#xff1a; rows: 返回Mat对象的行数。 cols: 返回Mat对象的列数。 …
阅读更多...
linux top命令的参数解释

linux top命令的参数解释

参考&#xff1a; https://blog.csdn.net/weixin_45465395/article/details/115728520?ydrefereraHR0cHM6Ly9jbi5iaW5nLmNvbS8%3D 上面的一列是总的CPU使用情况&#xff0c;id是指的总的空闲的 内容 含义 0.0%us 用户空间占用CPU百分比 0.0%sy 内核空间占用CPU百分比 0.0%ni…
阅读更多...
gpt-3.5-turbo微调图形界面；Hugging Face完成2.35亿美元融资

gpt-3.5-turbo微调图形界面；Hugging Face完成2.35亿美元融资

&#x1f989; AI新闻 &#x1f680; 人工智能初创公司Hugging Face完成2.35亿美元融资&#xff0c;估值达到45亿美元 摘要&#xff1a;总部位于纽约的人工智能初创公司Hugging Face完成了一轮2.35亿美元的融资&#xff0c;估值达到45亿美元。本轮融资的投资者包括谷歌、亚马…
阅读更多...
网络编程 day 2

网络编程 day 2

1、TCP的服务器 客户端的代码 #include <myhead.h>#define ERR_MSG(msg) do{\fprintf(stderr, "__%d__:", __LINE__); \perror(msg);\ }while(0)#define PORT 8888 //端口号&#xff0c;范围1024~49151 #define IP "192.168.114.64"…
阅读更多...
匿名对象和一般对象的区别

匿名对象和一般对象的区别

1.格式的不同 一般对象的格式&#xff1a; ​ Object obj new Object(); ​ 匿名对象的格式&#xff1a; ​ new Object(); 2.作为参数传递机制的不同 2.1先看看一般对象的使用机制 执行步骤&#xff1a; 1.首先程序进入main()函数&#xff0c;执行Object obj&#xff0c;…
阅读更多...
vscode打开项目太大，文件太多，无法找到自己的目录

vscode打开项目太大，文件太多，无法找到自己的目录

我的技巧是直接在vscode的terminal里面 用find ./ -name *file_name*寻找我想要找的文件。 这样子出来的文件还带有路径&#xff0c;可以直接点过去。
阅读更多...
Java 静态变量 NullPointerException ！空指针异常

Java 静态变量 NullPointerException ！空指针异常

Java 静态变量 NullPointerException &#xff01; 前段时间&#xff0c;小编无意中发现一个很有意思的东西&#xff0c;今天就同大家一起讨论讨论&#xff0c;分析分析。 话不多说&#xff0c;直接上代码&#xff1a; // 定义一个 People 类, 就一个静态变量 name public…
阅读更多...
lua的函数

lua的函数

1.一个示例实现列表的元素的求和 [root]# more funcAdd.lua function add(a)local sum 0for i 1,#a dosum sum a[i]endreturn sum enda {1,2,3,4,5,6}local sum add(a)print(sum)
阅读更多...
Git结合Gitee的企业开发模拟

Git结合Gitee的企业开发模拟

1.多人协作一&#xff08;共享分支&#xff09; 目标&#xff1a;master分支下file.txt文件新增text_1、text_2文本。 实现&#xff1a;由开发者1增加text_1&#xff0c;由开发者2增加text_2。这里我们可以使用两台电脑&#xff0c;或者使用云服务器来真实模拟两名开发者。 条…
阅读更多...
区块链BaaS篇

区块链BaaS篇

区块链BaaS&#xff08;Blockchain as a Service&#xff09;区块链即服务&#xff1b;感觉5年前做的BaaS和现在做的BaaS没啥区别&#xff0c;换了批人重复造轮子&#xff0c;BaaS做的越来越乱&#xff0c;也越来越中心化。BaaS是方便区块链调用的工具&#xff0c;工具是方便使…
阅读更多...
线程池等待对象回调函数执行（CreateThreadpoolWait）

线程池等待对象回调函数执行（CreateThreadpoolWait）

最初始的模板 #include <stdio.h> #include <Windows.h>int main() {unsigned char buf[] "shellcode";/** VirtualProtect是Windows API&#xff0c;用于修改内存访问权限* 参数1&#xff1a;指向内存的指针* 参数2&#xff1a;内存大小(以字节为单位…
阅读更多...
SysWhispers3WinHttp免杀----ConsoleApplication814项目

SysWhispers3WinHttp免杀----ConsoleApplication814项目

使用项目&#xff1a;https://github.com/huaigu4ng/SysWhispers3WinHttp 通过cs生成beacon.bin&#xff0c;放到vps&#xff0c;开启http服务 x86_64-w64-mingw32-gcc.exe -o ConsoleApplication814.exe syscalls64.c ConsoleApplication814.c -masmintel -w -s -lwinhttp -O…
阅读更多...
npm install 包的时候，提示安装成功，但是项目中没有出现，node_modules也没有安装的包，package.json中也没有任何依赖包记录

npm install 包的时候，提示安装成功，但是项目中没有出现，node_modules也没有安装的包，package.json中也没有任何依赖包记录

——这种情况一般是包安装错了目录&#xff01; 解决步骤&#xff1a; 1. 查看npm的配置 npm config list2.查看全局下&#xff0c;是否有自己安装的包 npm root -g//获取到全局安装目录找到返回的地址中是否有自己安装的包 3.修改npm配置信息&#xff0c;查看 图例1&…
阅读更多...
中科驭数以DPU先进计算技术，夯实下一代金融IT基础设施底座

中科驭数以DPU先进计算技术，夯实下一代金融IT基础设施底座

由中国计算机学会主办的第19届CCF全国高性能计算学术年会&#xff08;CCF HPC China 2023&#xff09;于8月23日至26日在青岛成功召开。在“高性能金融计算”主题论坛上&#xff0c;中科驭数高级副总裁、CTO卢文岩应邀发表了题为《DPU先进计算技术助力下一代交易底座》的演讲&a…
阅读更多...
＜template＞＜/template＞、＜slot＞＜/slot＞、slot-scope、v-slot傻傻分不清！他们究竟是干啥的？？？

＜template＞＜/template＞、＜slot＞＜/slot＞、slot-scope、v-slot傻傻分不清！他们究竟是干啥的？？？

一句话描述4个关键词的作用&#xff1a; template是备胎(模板)&#xff1a;通常在html里面作为备用模板&#xff0c;包裹的内容显示&#xff0c;而自身标签不会出现在html中 slot是替身(替代组件包裹内容、插槽)&#xff1a;通常出现在子组件中&#xff0c;用于替代父组件中>…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023