文章目录
- 前言
- 一、神经网络原理
- 1、输入层
- 2、全连接层
- 3、激活函数
- 4、损失函数
- 5、前向传播
- 6、反向传播
- 二、Python实战神经网络
- 1. 权重初始化技巧
- 2. 梯度问题技巧
- 3. 模型泛化技巧
- 总结
前言
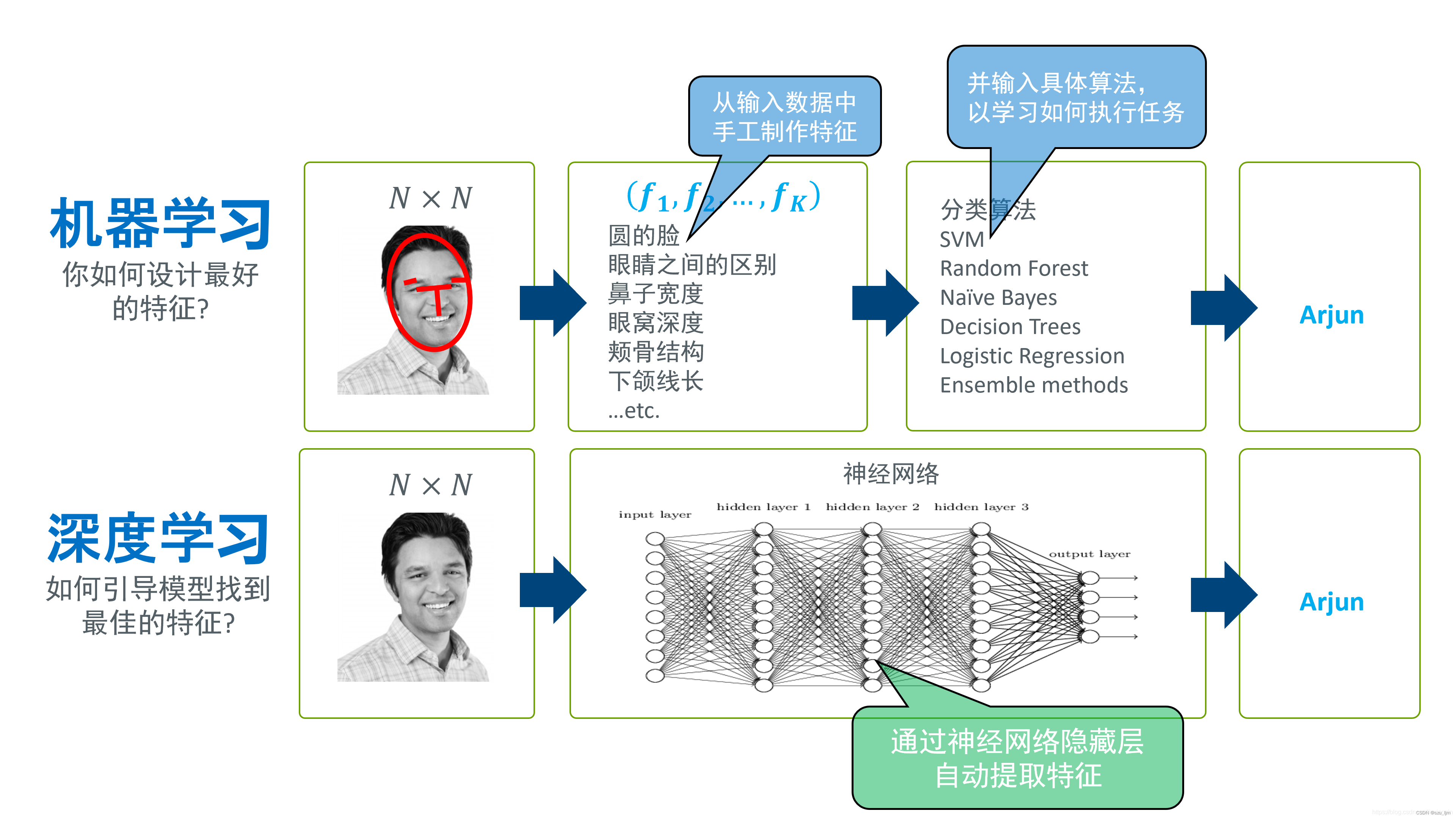
如果说机器学习是人工智能的皇冠,深度学习就是这顶皇冠上的明珠,深度学习的出现为人工智能领域的发展拉开了新的序幕。与常见的机器学习模型不同的是,深度学习的数据量更大,特征参数更多,但更重要的是深度学习不需要人为准备特征,神经网络会提取数据,并且不需要人为干预参数,学习过程会自动生成参数,调整参数,直到完成任务的效果达到最佳 。
以目标检测为例:机器学习需要规定图片的像素,长宽比例,物体轮廓,合格的参数等。而深度学习的卷积神经对图片卷积,池化提取各种特征,正向传播,反向传播调整参数,整个过程需要人为参与调整参数。
一、神经网络原理
1、输入层
神经网络的输入层是神经网络中的第一层,它负责接收输入数据并将其传递到神经网络的后续层中进行处理。输入层的神经元通常不进行任何计算或转换,它们只是简单地将输入数据传递到下一层。
输入层通常由一组神经元组成,每个神经元对应输入数据中的一个特征或变量。例如,在一个图像分类任务中,输入层的每个神经元可能对应一个像素点或者一个图像的特征。用MINST数据集训练神经网络模型时,MINST图像有784个像素,对应784个神经元组成的输入层。
2、全连接层
神经网络的全连接层,也称为密集连接层(Dense layer),是神经网络中隐藏层的常见类型。它的每个神经元都与前一层的所有神经元相连,因此也被称为全连接层。
在全连接层中,每个神经元都有一组权重 w w w 和一个偏置值 b b b ,这些权重和偏置值可以在训练过程中进行自适应调整,以使得神经网络可以更好地拟合训练数据。全连接层的输入是前一层的输出,经过权重和偏置的线性变换后,再经过一个非线性激活函数,得到输出结果。常见的激活函数包括sigmoid、ReLU、tanh等。
全连接层通常用于对数据进行特征提取和分类等任务,在不断的 w w w 和 b b b 线性组合和非线性变换中,全连接层能不断提取从低维到高维的特征。
3、激活函数
在神经网络中,激活函数主要起着增加模型的非线性分割能力、提高模型鲁棒性、缓解梯度消失问题的作用 ,可以对特征数据进行非线性映射和变换,比如 S i g m o i d Sigmoid Sigmoid函数可以将特征输入映射成概率,但在两侧会出现梯度消失的问题,会影响后续反向传播对权重矩阵进行更新的过程
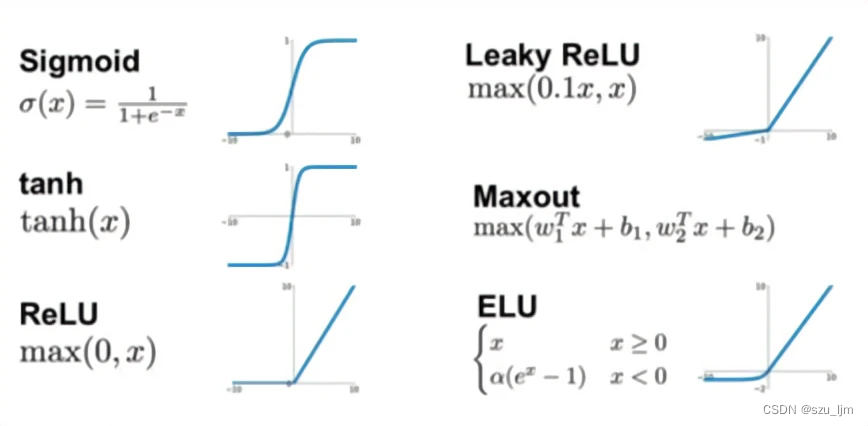
激活函数通过对权重 w w w 和偏置 b b b 的线性组合进行非线性映射可以输出激活值 a a a,例如ReLU激活函数的激活值 a a a 会成为下一层神经元的输入,以此类推
a = m a x ( 0 , w T x + b ) a = max(0, w^{T}x + b) a=max(0,wTx+b)
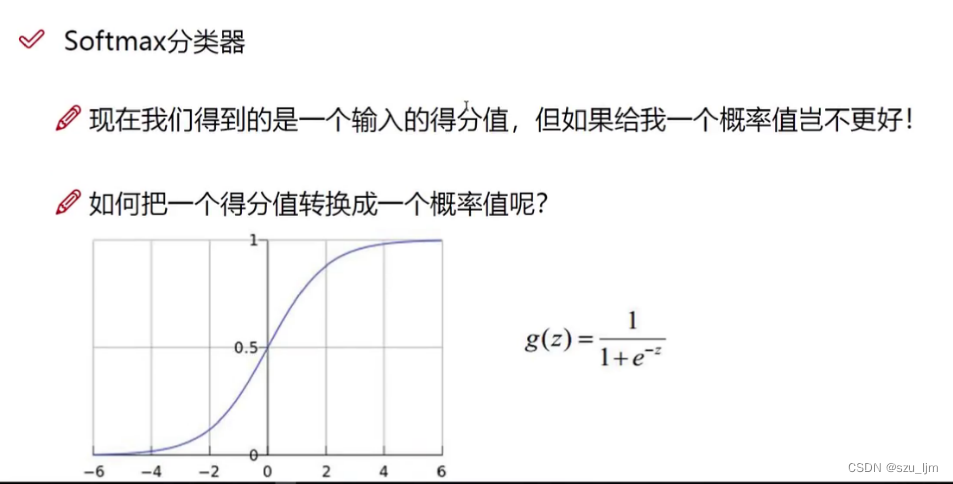
Softmax函数是一种常用的激活函数,通常用于多分类问题中。给定一个向量
z
=
(
z
1
,
z
2
,
.
.
.
,
z
k
)
z = (z_1, z_2, ..., z_k)
z=(z1,z2,...,zk),Softmax函数将其转化为一个概率分布向量
p
=
(
p
1
,
p
2
,
.
.
.
,
p
k
)
p = (p_1, p_2, ..., p_k)
p=(p1,p2,...,pk),其中每个元素
p
i
p_i
pi 表示在所有元素的指数函数归一化后,
z
i
z_i
zi 对应的概率值。Softmax函数的表达式如下:
p i = e z i ∑ j = 1 k e z j , f o r i = 1 , 2 , . . . , k p_i = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}}, \ \ \ \ \ \ for \ \ i=1,2,...,k pi=∑j=1kezjezi, for i=1,2,...,k
Softmax函数的输出是一个概率分布向量,其中每个元素都在 0 到 1 之间,且所有元素之和为 1。这样可以使得 Softmax 函数的输出可以直接用作多分类问题的预测结果。
4、损失函数
神经网络的损失函数,也称为目标函数或代价函数,是用于衡量神经网络预测结果与实际结果之间差距的函数。神经网络的目标是通过最小化损失函数来优化模型参数,使得神经网络可以更好地拟合训练数据,并在测试数据上实现较好的泛化能力。
神经网络的损失函数可以根据不同的任务类型和模型结构而不同。一些常见的损失函数有:均方误差(Mean Squared Error,MSE)、交叉熵损失函数(Cross-Entropy Loss)、对数损失函数(Log Loss)、Hinge Loss、KL 散度损失函数(Kullback-Leibler Divergence Loss)

平方损失函数最简单,平方损失函数计算出的误差值恒大于0。平方损失函数能放大网络的大误差带来的影响,缩小网络的小误差带来的影响。我们用
C
C
C 表达平方损失值 ,
y
i
y_{i}
yi 表示真实标签值,
y
^
i
\hat y_{i}
y^i 表示神经网络输出值,也就是神经元的激活值
a
a
a
C
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
C = \frac{1}{n} \sum_{i=1} ^{n} (y_{i} - \hat y_{i})^2
C=n1i=1∑n(yi−y^i)2
交叉熵损失函数可以降低神经元饱和对学习速度的影响,在计算上我们对 y i y_{i} yi 取对数,等价于对损失值取指数,所以在梯度下降时对 y i y_{i} yi 求偏导后更新的速率会变快,交叉熵损失越大,神经网络的学习速度就越快
C = − 1 n ∑ i = 1 n [ y i l n y ^ i + ( 1 − y i ) l n ( 1 − y ^ i ) ] C = -\frac{1}{n} \sum_{i=1}^n[y_{i} ln \hat y_{i} + (1 - y_{i}) ln(1 - \hat y_{i})] C=−n1i=1∑n[yilny^i+(1−yi)ln(1−y^i)]
5、前向传播
神经网络的前向传播是指从输入数据开始,通过一系列的计算和变换,最终得到神经网络的输出结果的过程。下面是一个简单的神经网络前向传播的过程:
输入层:将输入数据传递到神经网络的第一层,也称为输入层。
隐藏层:神经网络的中间层,通过一系列的计算和变换,将输入数据转换为更具有表达能力的特征表示,并将其传递到下一层。
输出层:神经网络的最后一层,将隐藏层的输出进一步处理,得到神经网络的最终输出结果。
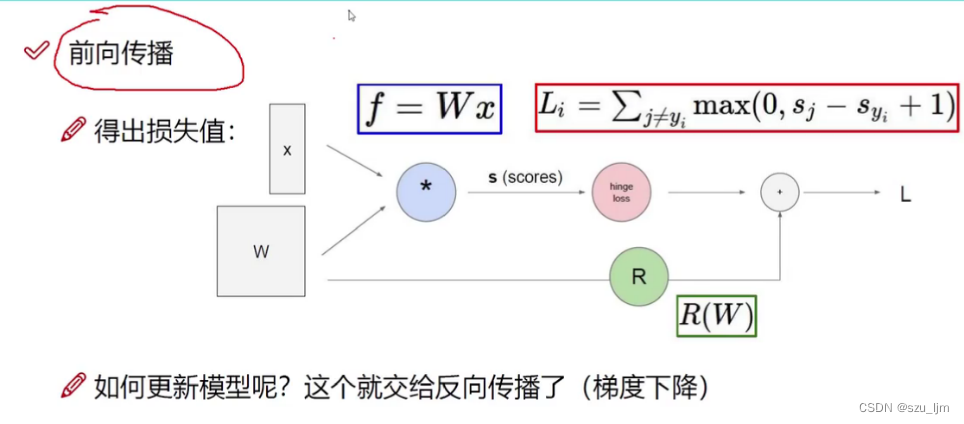
在每个层中,包含一个或多个神经元,每个神经元都有自己的权重和偏置,用于计算输入数据的加权和,并通过激活函数进行非线性变换。这些计算和变换的过程可以表示为以下公式:
z
i
=
∑
j
=
1
n
w
i
j
x
j
+
b
i
z_{i} = \sum^{n}_{j=1}w_{ij}x_{j} + b_{i}
zi=j=1∑nwijxj+bi
y
i
=
f
(
z
i
)
y_{i} = f(z_{i})
yi=f(zi)
其中, z i z_i zi表示第 i i i个神经元的加权和, w i j w_{ij} wij表示第 i i i个神经元与第 j j j个输入的权重, x j x_j xj表示第 j j j个输入, b i b_i bi表示第 i i i个神经元的偏置, f f f表示激活函数, y i y_i yi表示第 i i i个神经元的输出。
h
=
R
e
L
U
(
w
1
∗
x
+
b
1
)
h = ReLU(w1 * x + b1)
h=ReLU(w1∗x+b1)
y
=
w
2
∗
h
+
b
2
y = w2 * h + b2
y=w2∗h+b2
在前向传播的过程中,每个神经元的输出都会作为下一层神经元的输入,逐层传递,直到到达输出层,得到神经网络的最终输出结果。
6、反向传播
神经网络的反向传播(Backpropagation)是一种用于训练神经网络的优化算法,其基本思想是通过计算损失函数对神经网络参数的梯度来更新参数,使得神经网络的预测结果更加准确
反向传播的第一步是计算损失,将神经网络的输出结果与真实值进行比较,经过损失函数计算映射出损失值,反向传播想要达到的最终效果也就是降低整个网络预测结果的损失。
l
o
s
s
=
f
(
y
i
,
y
^
i
)
loss = f(y_{i}, \hat y_{i})
loss=f(yi,y^i)
L
=
(
y
−
t
)
2
L = (y - t)^2
L=(y−t)2
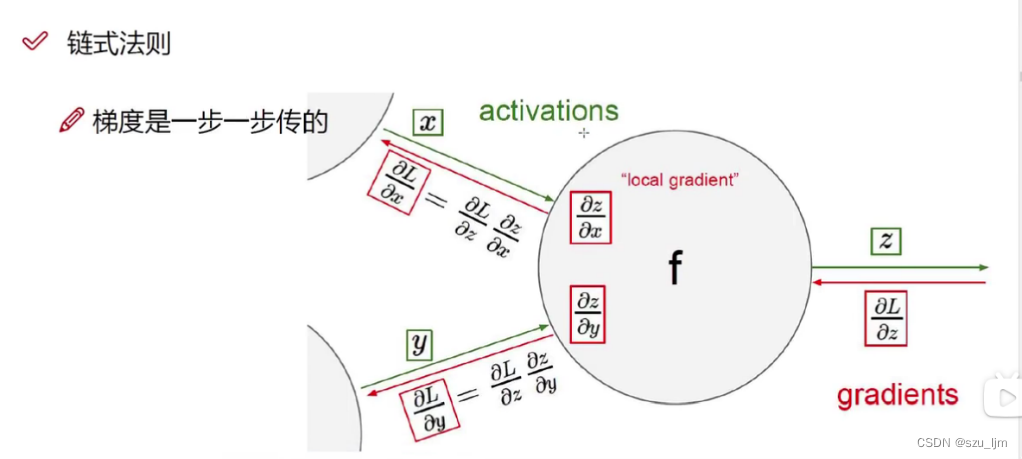
根据反向传播的链式求导法则,我们用损失函数
L
L
L 对网络参数求导,不同
L
a
y
e
r
s
Layers
Layers 之间的求导需要按照复合函数求导法则,进行梯度的链式计算
d
L
d
w
2
=
d
L
d
y
∗
d
y
d
w
2
\frac{dL}{dw_{2}} = \frac{dL}{dy} * \frac{dy}{dw_{2}}
dw2dL=dydL∗dw2dy
d
L
d
b
2
=
d
L
d
y
∗
d
y
d
b
2
\frac{dL}{db_{2}} = \frac{dL}{dy} * \frac{dy}{db_{2}}
db2dL=dydL∗db2dy
d
L
d
w
1
=
d
L
d
y
∗
d
y
d
h
∗
d
h
d
w
1
\frac{dL}{dw_{1}} = \frac{dL}{dy} * \frac{dy}{dh} * \frac{dh}{dw_{1}}
dw1dL=dydL∗dhdy∗dw1dh
d
L
d
b
1
=
d
L
d
y
∗
d
y
d
h
∗
d
h
d
b
1
\frac{dL}{db_{1}} = \frac{dL}{dy} * \frac{dy}{dh} * \frac{dh}{db_{1}}
db1dL=dydL∗dhdy∗db1dh
将所求的梯度乘上学习率
η
\eta
η 作为权重更新的步长来优化网络参数减小误差,学习率
η
\eta
η 过大会导致权重更新过快偏离最优解值,学习率
η
\eta
η 过小会导致网络更新学习速率低
w
2
′
=
w
2
−
η
∗
d
L
d
w
2
w2' = w2 - \eta * \frac{dL}{dw_{2}}
w2′=w2−η∗dw2dL
b
2
′
=
b
2
−
η
∗
d
L
d
b
2
b2' = b2 - \eta * \frac{dL}{db_{2}}
b2′=b2−η∗db2dL
w
1
′
=
w
1
−
η
∗
d
L
d
w
1
w1' = w1 - \eta * \frac{dL}{dw_{1}}
w1′=w1−η∗dw1dL
b
1
′
=
b
1
−
η
∗
d
L
d
b
1
b1' = b1 - \eta * \frac{dL}{db_{1}}
b1′=b1−η∗db1dL
前向传播和反向传播过程不断重复循环,就可以不断减小误差,提高正确率,获得学习效果比较好的网络模型
二、Python实战神经网络

初次用Python实战神经网络,我们调用keras和Tensorflow深度学习库作为开发接口,简化神经网络的训练过程,下面我们用到知名的mnist数据集做手写数字识别。
首先是导包,并将mnist数据集划分为训练集和验证集,接着将28*28的二位像素图拉伸成784的一维数组并将像素数据转为浮点数,然后开始搭建网络框架,第一层是有64个sigmoid神经元,第二层有10个softmax神经元输出概率,指定使用SGD梯度下降方法和交叉熵损失函数,设置好batch_size和epochs,将训练集扔进网络就可以开始训练了
import keras
from tensorflow.keras.optimizers import SGD
from keras.models import Sequential
from keras.datasets import mnist
from keras.layers import Dense, Activation
from keras.initializers import glorot_normal, glorot_uniform, Zeros, RandomNormal
import matplotlib.pyplot as plt
(X_train, y_train), (X_valid, y_valid) = mnist.load_data()
plt.figure(figsize=(12, 8))
for k in range(12):
plt.subplot(3, 4, k+1)
plt.imshow(X_train[k], cmap='Greys')
plt.axis('off')
plt.tight_layout()
plt.show()
X_train = X_train.reshape(60000, 784).astype('float32')
X_valid = X_valid.reshape(10000, 784).astype('float32')
X_train /= 255
X_valid /= 255
n_classes = 10
y_train = keras.utils.to_categorical(y_train, n_classes)
y_valid = keras.utils.to_categorical(y_valid, n_classes)
model = Sequential()
model.add(Dense(64, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
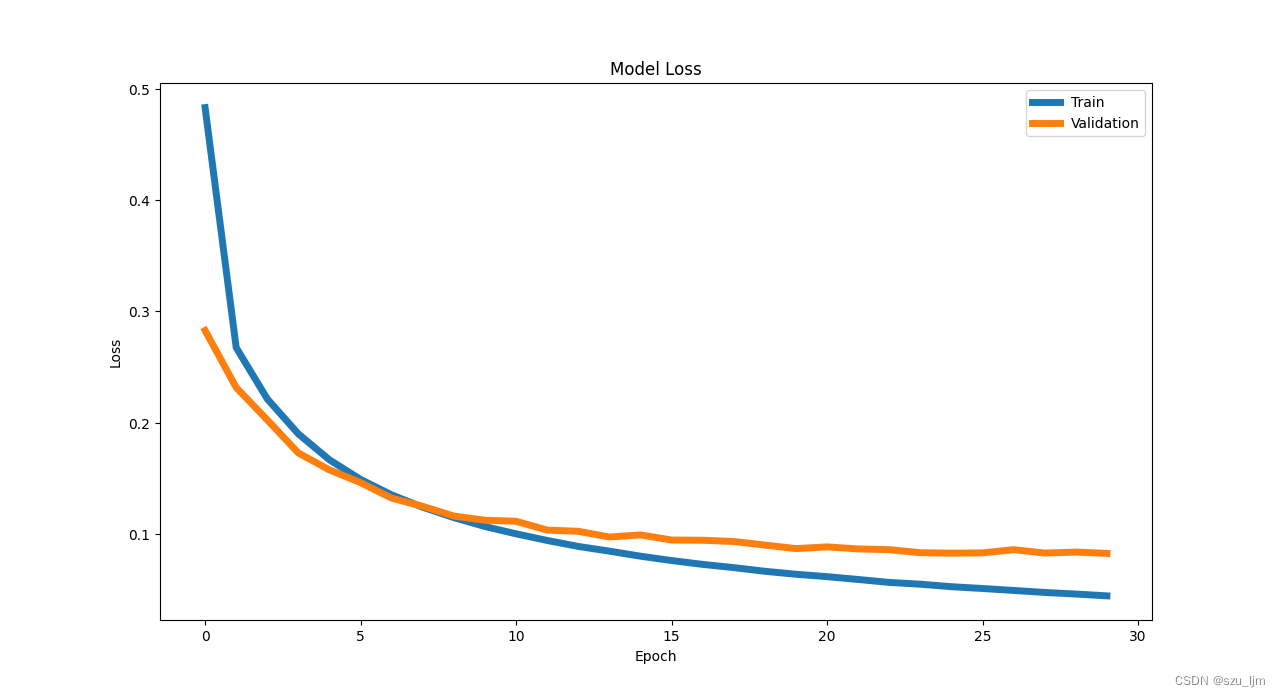
history = model.fit(X_train, y_train, batch_size=128, epochs=30, verbose=1, validation_data=(X_valid, y_valid))
plt.figure(figsize=(12, 8))
plt.plot(history.history['loss'], linewidth=5)
plt.plot(history.history['val_loss'], linewidth=5)
plt.title('Model Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.show()
1. 权重初始化技巧
在训练神经网络时,参数 w w w 和 b b b 是用随机值来初始化的,绝对值过大过小的 w w w 和 b b b 加权后 z z z 越接近无穷,导致激活值越趋近于0或1,梯度的变化率越小,神经元饱和更新速率越低。所以在权重初始化时,我们常采用Glorot正态分布对 w w w 进行采样,这样激活值分布在0.5附近较多,梯度变化最快,更新速率高,当然也可以采样Glorot均匀分布进行采样。
import keras
from keras.datasets import mnist
from tensorflow.keras.optimizers import SGD
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.initializers import glorot_normal, glorot_uniform, Zeros, RandomNormal, Ones
import matplotlib.pyplot as plt
(X_train, y_train), (X_valid, y_valid) = mnist.load_data()
X_train = X_train.reshape(60000, 784).astype('float32')
X_valid = X_valid.reshape(10000, 784).astype('float32')
X_train /= 255
X_valid /= 255
n_classes = 10
y_train = keras.utils.to_categorical(y_train, n_classes)
y_valid = keras.utils.to_categorical(y_valid, n_classes)
n_input = 784
n_dense = 128
b_init = Zeros()
w1_init = Ones()
w2_init = RandomNormal(stddev=1.0)
model1 = Sequential()
model2 = Sequential()
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w1_init, bias_initializer=b_init))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w2_init, bias_initializer=b_init))
model1.add(Activation('sigmoid'))
model2.add(Activation('sigmoid'))
model1.add(Dense(10, activation='softmax'))
model2.add(Dense(10, activation='softmax'))
model1.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
model2.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
history1 = model1.fit(X_train, y_train, batch_size=128, epochs=30, verbose=1, validation_data=(X_valid, y_valid))
history2 = model2.fit(X_train, y_train, batch_size=128, epochs=30, verbose=1, validation_data=(X_valid, y_valid))
plt.figure(figsize=(12, 8))
plt.plot(history1.history['loss'], linewidth=5)
plt.plot(history2.history['loss'], linewidth=5)
plt.title('Model Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(['w_ones_init', 'w_normal_init'], loc='upper right')
plt.show()
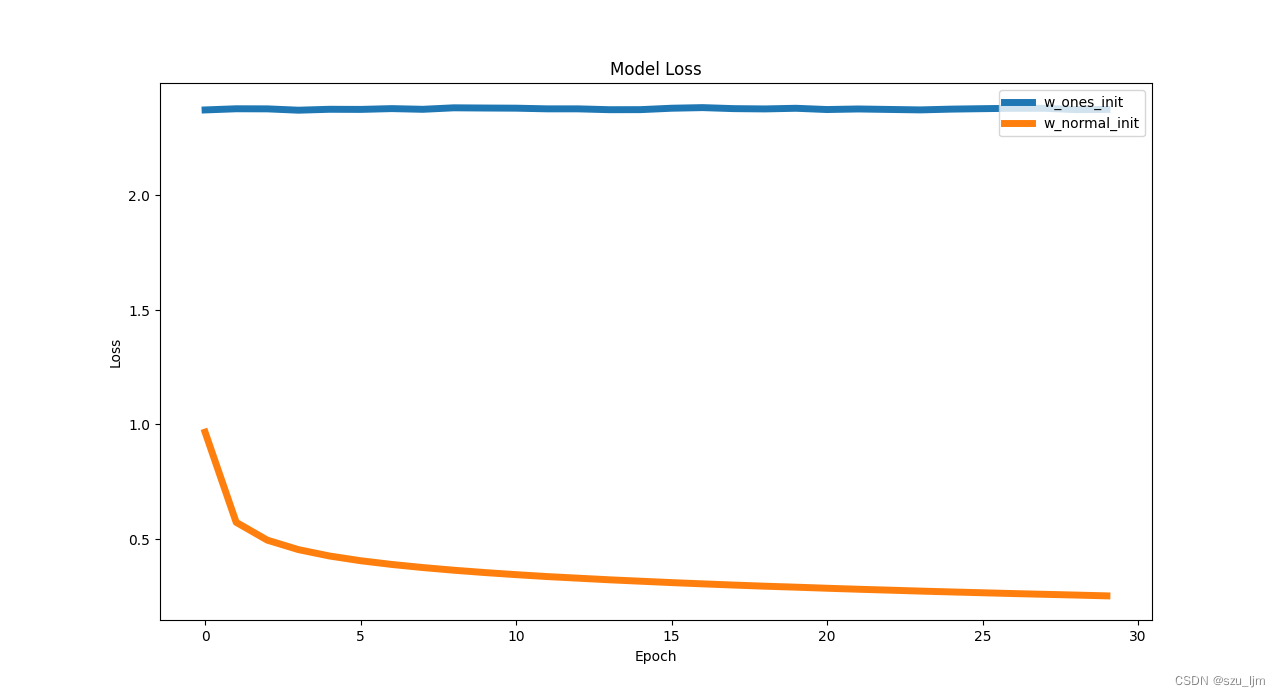
从上述对比实验可以发现,不同的权重初始化方法会影响网络学习效果,服从正态分布采样的
w
w
w 的模型
l
o
s
s
loss
loss 降低得更快,而
w
w
w 都初始化为1的模型
l
o
s
s
loss
loss 几乎难以下降
2. 梯度问题技巧
梯度问题主要分为梯度消失和梯度爆炸,而梯度消失问题更加普遍,刚刚我们也介绍了不合理的权重初始化会导致梯度消失的问题。按照反向传播的原理,离输出层越远的 L a y e r s Layers Layers 偏离理想化正态分布的可能性越高,更新效率越低。所以为了让每一层 L a y e r s Layers Layers 能够更好的学习,我们可以使用批量的归一化方法,对 L a y e r s Layers Layers 的激活值进行归一化让其逼近正态分布
import keras
from keras.datasets import mnist
from tensorflow.keras.optimizers import SGD
from keras.models import Sequential
from keras.layers import Dense, BatchNormalization
from keras.initializers import glorot_normal, glorot_uniform, Zeros, RandomNormal, Ones
import matplotlib.pyplot as plt
(X_train, y_train), (X_valid, y_valid) = mnist.load_data()
X_train = X_train.reshape(60000, 784).astype('float32')
X_valid = X_valid.reshape(10000, 784).astype('float32')
X_train /= 255
X_valid /= 255
n_classes = 10
y_train = keras.utils.to_categorical(y_train, n_classes)
y_valid = keras.utils.to_categorical(y_valid, n_classes)
n_input = 784
n_dense = 64
b_init = Zeros()
w_init = RandomNormal(stddev=1.0)
model1 = Sequential()
model2 = Sequential()
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='sigmoid'))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='sigmoid'))
model1.add(BatchNormalization())
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='sigmoid'))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='sigmoid'))
model1.add(BatchNormalization())
model1.add(Dense(10, activation='softmax'))
model2.add(Dense(10, activation='softmax'))
model1.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
model2.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
history1 = model1.fit(X_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(X_valid, y_valid))
history2 = model2.fit(X_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(X_valid, y_valid))
plt.figure(figsize=(12, 8))
plt.plot(history1.history['loss'], linewidth=5)
plt.plot(history2.history['loss'], linewidth=5)
plt.title('Model Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(['use batch_normalize', 'no batch_normalize'], loc='upper right')
plt.show()
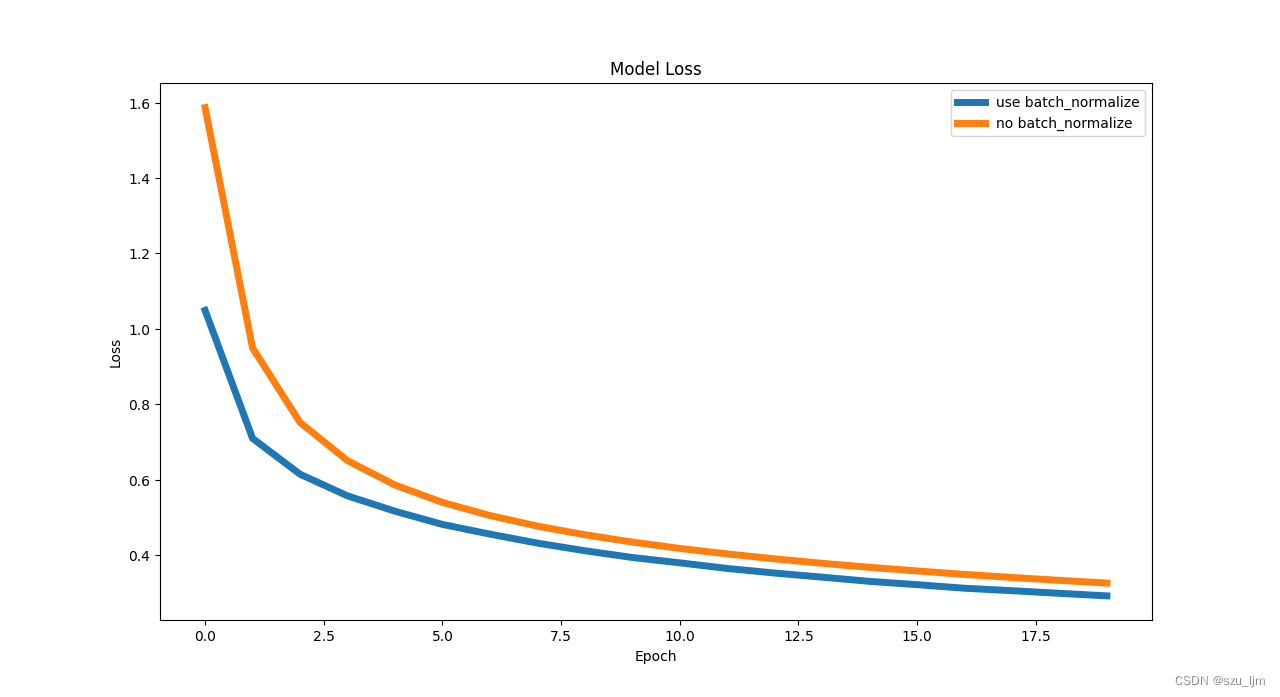
从上述对比实验可以发现,相同的权重初始化但使用BatchNormalization批量归一化方法会影响网络学习效果,对每层网络都进行批量归一化的模型
l
o
s
s
loss
loss 更小,而没有归一化的模型
l
o
s
s
loss
loss 相对较大
优化后的随机梯度下降(Stochastic Gradient Descent, SGD)是一种在传统SGD基础上进行改进的优化算法。经过改进的SGD方法可以更快地收敛,并具有更好的性能。以下是几种常见的优化后的SGD方法:
Momentum(动量):Momentum方法通过引入动量参数来加速收敛过程。它基于当前梯度和先前的更新方向来计算下一步的更新方向。动量参数决定了更新方向的权重,使得在梯度方向一致的情况下,更新幅度可以增加。这样可以在梯度方向波动较大的情况下,减少震荡,从而加速收敛。
Nesterov Accelerated Gradient(NAG):NAG是对Momentum方法的改进。与Momentum不同,NAG在计算梯度之前先进行一次"lookahead"更新,即先使用动量参数的方向进行一次更新,然后再计算梯度。这样可以获得更准确的梯度估计,从而提高了收敛速度和性能。
Adagrad:Adagrad根据参数的历史梯度信息来调整学习率。具体来说,Adagrad为每个参数维护一个逐元素平方的梯度累积量,并在更新时将其除以该累积量的平方根。这样可以使得学习率自适应地调整,对于频繁出现的梯度较大的参数,学习率会相应地减小,从而更加平缓地接近最优点。
RMSprop:RMSprop是对Adagrad方法的改进。Adagrad的一个问题是随着训练的进行,累积梯度平方的分母会越来越大,导致学习率过度下降。RMSprop通过引入衰减因子来解决这个问题,即对梯度平方做一个指数加权平均。这样可以限制累积梯度平方的增长,并提高算法的鲁棒性和收敛速度。
Adam:Adam是一种结合了动量和Adagrad/RMSprop的优点的优化算法。它综合考虑了梯度的一阶矩估计(均值)和二阶矩估计(方差),并在更新过程中自适应地调整学习率。Adam具有良好的收敛性和性能,在广泛的深度学习任务中被广泛使用。
3. 模型泛化技巧
神经网络在学习过程中容易出现过拟合现象,就是在训练集上表现不错,但在测试集却效果很差,没办法推广,所以模型的泛化能力和鲁棒性至关重要,我们可以通过正则化,数据增强,droupout等手段增强模型泛化能力,droupout的手段类似决策树中的剪枝策略,能有效降低过拟合程度
import keras
from keras.datasets import mnist
from tensorflow.keras.optimizers import SGD
from keras.models import Sequential
from keras.layers import Dense, BatchNormalization, Dropout
from keras.initializers import glorot_normal, glorot_uniform, Zeros, RandomNormal, Ones
import matplotlib.pyplot as plt
(X_train, y_train), (X_valid, y_valid) = mnist.load_data()
X_train = X_train.reshape(60000, 784).astype('float32')
X_valid = X_valid.reshape(10000, 784).astype('float32')
X_train /= 255
X_valid /= 255
n_classes = 10
y_train = keras.utils.to_categorical(y_train, n_classes)
y_valid = keras.utils.to_categorical(y_valid, n_classes)
n_input = 784
n_dense = 64
b_init = Zeros()
w_init = RandomNormal(stddev=1.0)
model1 = Sequential()
model2 = Sequential()
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model1.add(BatchNormalization())
model2.add(BatchNormalization())
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model1.add(BatchNormalization())
model2.add(BatchNormalization())
model1.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model2.add(Dense(n_dense, input_dim=n_input, kernel_initializer=w_init, bias_initializer=b_init, activation='relu'))
model1.add(BatchNormalization())
model1.add(Dropout(0.2))
model2.add(BatchNormalization())
model1.add(Dense(10, activation='softmax'))
model2.add(Dense(10, activation='softmax'))
model1.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model2.compile(loss='categorical_crossentropy', optimizer=SGD(learning_rate=0.1), metrics=['accuracy'])
history1 = model1.fit(X_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(X_valid, y_valid))
history2 = model2.fit(X_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(X_valid, y_valid))
plt.figure(figsize=(12, 8))
plt.subplot(121)
plt.plot(history1.history['loss'], linewidth=5)
plt.plot(history2.history['loss'], linewidth=5)
plt.title('Model Train Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(['use adam and dropout', 'no adam and dropout'], loc='upper right')
plt.subplot(122)
plt.plot(history1.history['val_loss'], linewidth=5)
plt.plot(history2.history['val_loss'], linewidth=5)
plt.title('Model Valid Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(['use adam and dropout', 'no adam and dropout'], loc='upper right')
plt.show()

从上述对比实验可以发现,使用dropoout方法和adam优化器会影响网络学习效果,无论在训练集还是测试集都会更好,adam优化器会让网络的更新学习速率更快,误差降低得更快,而dropoout方法降低了网络在测试集过拟合得风险,使得第一轮次的Valid Loss更小
总结
以上就是人工神经网络学习笔记的全部内容,本文简单介绍了神经网络的数学原理以及网络训练优化技巧。神经网络的概念受到了对生物神经系统的研究和理解的启发。神经网络的设计灵感来自于对大脑中神经元之间相互连接和信息传递的观察。神经网络是通过对生物神经系统的研究和理解得到的灵感,结合数学和计算机科学的方法构建的一种模型。它模拟了生物神经网络中神经元之间的连接和信息传递,通过学习和调整权重来实现对输入数据的处理和模式识别能力。