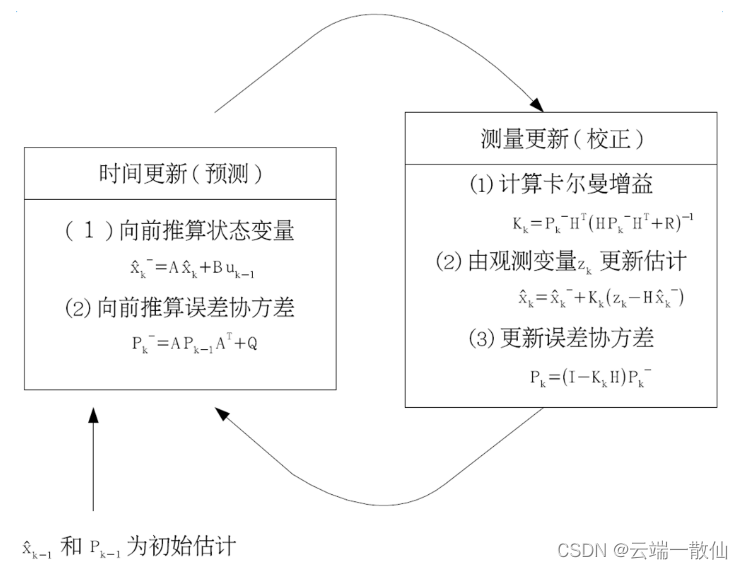
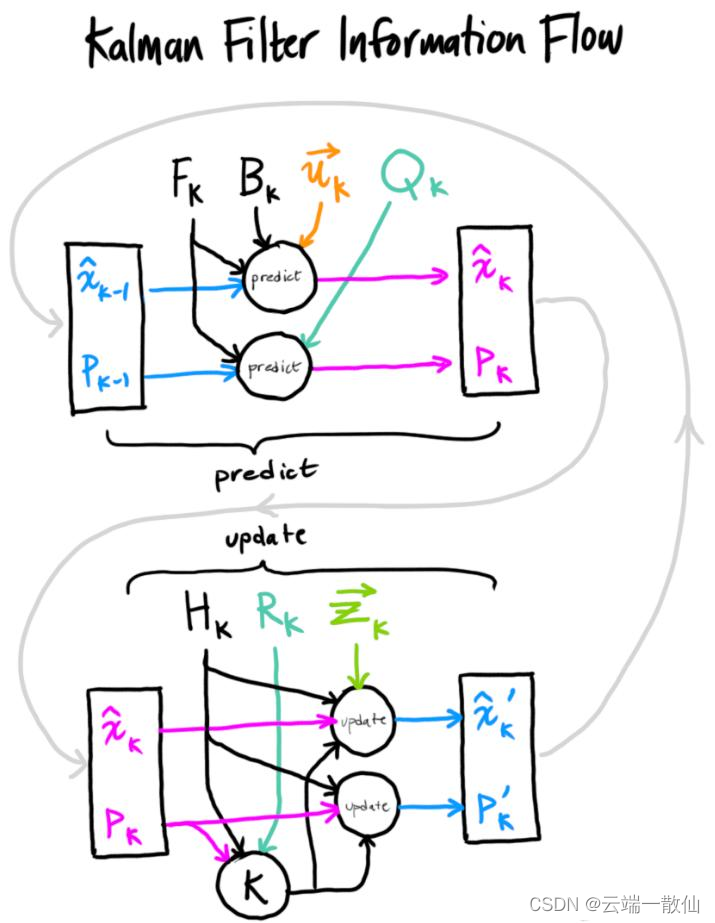
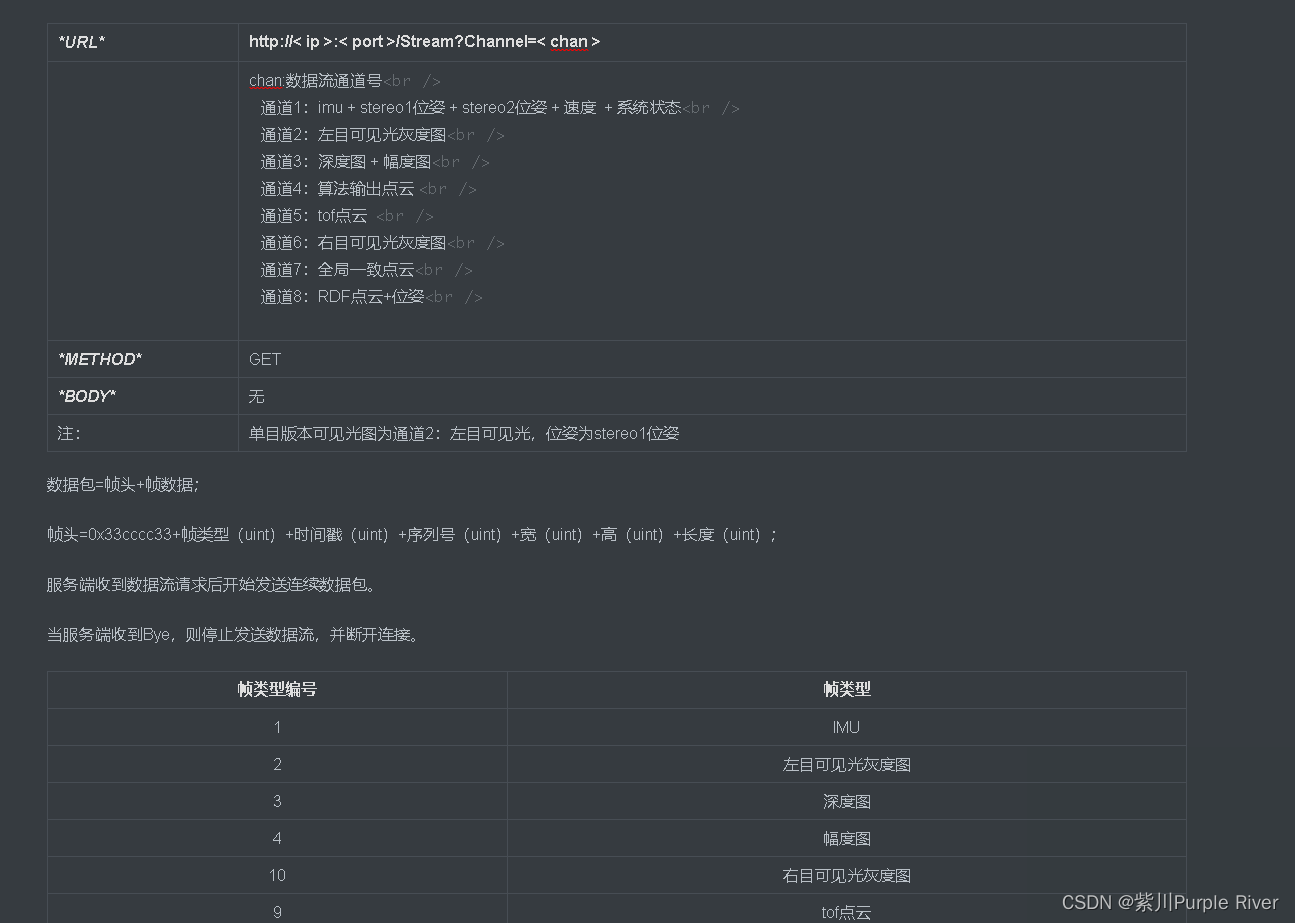
预测（prediction）

状态变量

$$x_k=A{x}_{k-1}+B{u}_{k-1}+w_{k-1}$$
其中n维向量$x_k$为k时刻的系统状态变量，n维向量 $x_{k-1}$是k-1时刻的系统状态变量。

$A$是状态转移矩阵或者过程增益矩阵，是$n\times n$阶方阵，它将k-1时刻状态和当前的k时刻状态联系起来。

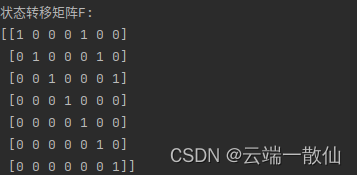
$B$是可选的控制输入$u\in R^l$的增益，在大多数实际情况下并没有控制增益，所以$B{u}_{k-1}$这一项很愉快的变成零了。

$w_{k-1}$是n维向量，代表过程激励噪声，它对应了中每个分量的噪声，是期望为0，协方差为Q的高斯白噪声，$w～N(0，Q)$

观测变量

$$z_k=H{x}_k+v_k$$
其中观测值$z_k$是m阶向量，状态变量$x_k$是n阶向量。对于目标检测，$z_k$就是检测结果转化后的值

观测矩阵$H$是$m\times n$阶矩阵，代表状态变量$x_k$对测量变量$z_k$的增益

观测噪声$v_k$是期望为0，协方差为R的高斯白噪声，$v_k～N(0,R)$

误差协方差

$${\hat{P}}_{\bar{k}}=A{\hat{P}}_{k-1}{A}^T+Q$$

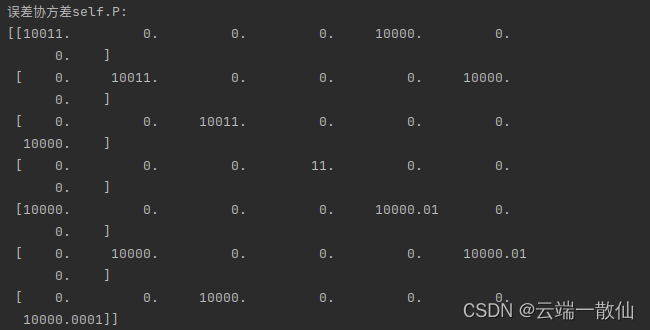
${\hat{P}}_{\bar{k}-1}$：表示k时刻的先验估计协方差，这个协方差矩阵只要确定了一开始的${\hat{P}}_0$，后面都可以递推出来，而且初始协方差矩阵${\hat{P}}_0$只要不是为0，它的取值对滤波效果影响很小，都能很快收敛。

${\hat{P}}_{\bar{k}}$：表示k时刻的后验估计协方差，是滤波结果之一。

$Q$：表示过程激励噪声的协方差，它是状态转移矩阵与实际过程之间的误差。这个矩阵是卡尔曼滤波中比较难确定的一个量，一般有两种思路：一是在某些稳定的过程可以假定它是固定的矩阵，通过寻找最优的Q值使滤波器获得更好的性能，这是调整滤波器参数的主要手段，Q一般是对角阵，且对角线上的值很小，便于快速收敛；二是在自适应卡尔曼滤波（AKF）中Q矩阵是随时间变化的。

更新（update/correction）

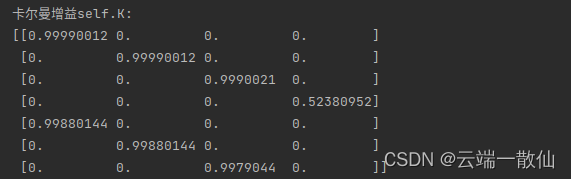
卡尔曼增益

$$K_k=\frac{{\hat{P}}_{\bar{k}}{H}^T}{H{\hat{P}}_{\bar{k}}{H}^T+R}$$

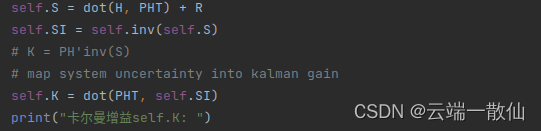
$H$：表示量测矩阵，是$m\times n$阶矩阵，它把m维测量值转换到n维与状态变量相对应。

$R$：测量噪声的协方差矩阵，这个值过大过小都会使滤波效果变差，且取值越小，收敛越快。

由观测变量$z_k$更新估计

$${\hat{x}}_k={\hat{x}}_{\bar{k}}+K_k(z_k-H{\hat{x}}_{\bar{k}})$$

${\hat{x}}_{\bar{k}}$：表示$k$时刻先验状态估计值，这是算法根据前次迭代结果（就是上一次循环的后验估计值）做出的不可靠估计。

${\hat{x}}_k$：表示k时刻后验状态估计值，也就是要输出的该时刻最优估计值，这个值是卡尔曼滤波的结果。

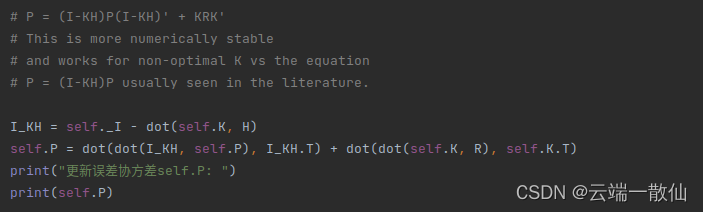
更新误差协方差

$${\hat{P}}_k=(I-K_{k}H){\hat{P}}_{\bar{k}}$$

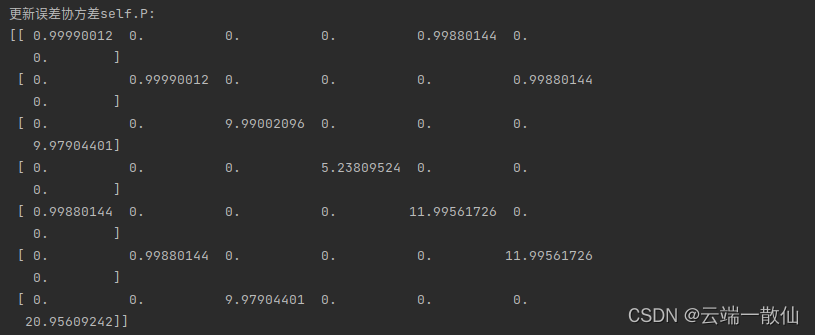
新的最佳估计是基于原最佳估计和已知外部影响校正后得到的预测。

新的不确定性是基于原不确定性和外部环境的不确定性得到的预测。