文章目录
- 前言
- 1. 括号匹配问题
- 2. 最小栈问题
- 3. 最大栈
- 总结
前言
提示:如果让我送给年轻人四个字,就是:量力而行。 量力而行不会失眠,不会啃老,不会为各种考试焦虑。顺其自然活得轻松。其实,量力而行最易大展宏图。
栈在常见的数据结构中也是比较常用的,一些经典的题目对于理解栈很有帮助,就那他们练手吧
1. 括号匹配问题
栈的典型题目,栈常用在括号匹配,表达式计算等等,我看就来看看这个最经典的问题:
参考题目介绍:20. 有效的括号 - 力扣(LeetCode)


对于这个题目来说,还是比较简单的,要处理的问题难题时判断符号是否一组,我们可以先用Hash将所有的符合存储下来,左半边就做key,右半边做value。遍历字符串的时候,遇到左半边符号就入栈,遇到右半边的符号就与栈顶的符号进行比较,不匹配就返回false;
public static boolean isValid(String s) {
if (s.length() < 2) {
return false;
}
HashMap<Character, Character> map = new HashMap<Character, Character>();
map.put('[', ']');
map.put('(', ')');
map.put('{', '}');
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (map.containsKey(c)) {
stack.push(c);
} else {
if (!stack.isEmpty()) {
// 拿到栈顶的左括号
Character left = stack.pop();
Character right = map.get(left);
if (right != c) {
return false;
}
} else {
return false;
}
}
}
return stack.isEmpty();
}
当然类似的题目还有很多,有难有易,可以多杀杀,挫挫锐气哈哈哈🤣,这里我就不一一举例🌰了
2. 最小栈问题
参考题目介绍:155. 最小栈 - 力扣(LeetCode)

不知到你会不会和我一样题目还没理解什么意思的,别慌,那我们就来看看,这个题要怎么解。我觉得本题的关键在于getMin()到底表示什么,我们可以画一个图;
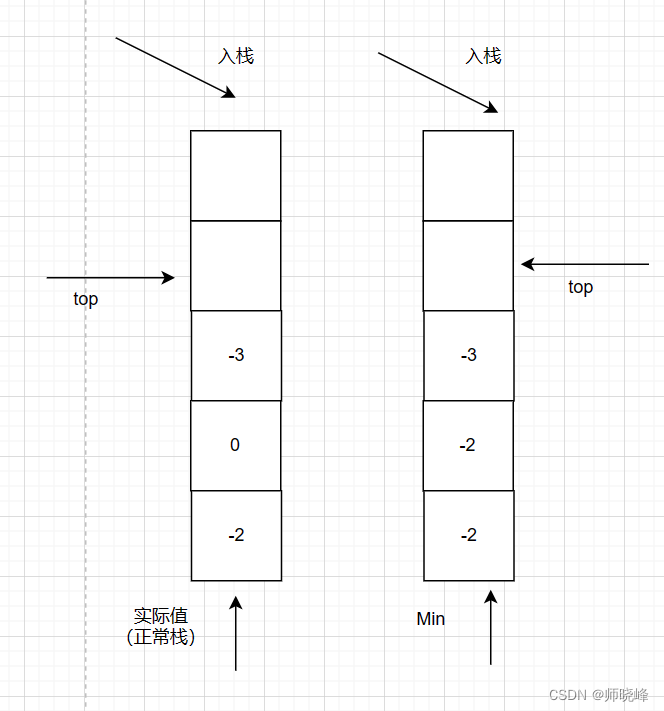
我们看到这个图,大致已经有了思路,Min栈内,中间-2元素,对它的理解就是解题的关键。
题目要求在常数时间内获取到栈中的最小值,也就是我们不能在getMin()的时候去计算,而是直接返回值,也就说只能在push和pop中做一些操作了。
栈的特性时先进后出,这个很重要,我们可以这么做,我们将元素(a)存入栈中的时候,就把当前的最小值(m)记录下来,也就是说如果a时栈顶,最小是就是m,我们可以直接返回。
这样的话我们就可以设计一个数据结构,使得每个元素a与其相应的最小值m时刻保持一致,所以我们需要一个辅助栈,与元素栈插入和删除保持一致,用来存储每个元素对应的最小值。
- 当元素要入栈的时候,我们取当前辅助栈的栈顶元素与之比较,该元素小,就将这个值存入辅助栈中;
- 当一个元素要出栈时,我们把辅助栈的栈顶元素一并出栈
这样的话,在任意时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
这样的话代码写起来就非常简单了🤣
class MinStack {
private static Stack<Integer> xStack;
private static Stack<Integer> minStack;
public MinStack() {
xStack = new Stack<>();
minStack = new Stack<>();
// 占位符
minStack.push(Integer.MAX_VALUE);
}
public void push(int val) {
xStack.push(val);
minStack.push(Math.min(val,minStack.peek()));
}
public void pop() {
xStack.pop();
minStack.pop();
}
public int top() {
return xStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/
有最小栈那会不会有最大栈呢?哈哈哈,他来了
3. 最大栈
参考题目介绍:716. 最大栈 - 力扣(LeetCode)
设计一个最大栈数据结构,及支持栈操作,有支持查找栈中最大元素。

这个题和上一题相反,处理方法上一致,一个普通的栈可以支持前三种操作,push(x),pop()和top(),这里我们需要考虑的是后面的操作peekMax()和popMax()。
对于peekMax(),我们可以用另一个栈来存储每个位置对应的最大值,比如第一个栈的元素为[2,1,5,3,9],那么第二个栈的元素就是[2,2,5,5,9]。在push(x)操作时,只需要将第二个栈顶元素和x的最大值入栈就行,而pop()操作只需要将第二个栈进行出栈。
对于popMax(),由于我们指导当前栈中最大元素值,我们就可以将两个栈同时出栈,并存储第一个栈出栈的所有值。当某个时刻第一个栈中的出栈元素等于当前栈中的最大值时,我们就找到了最大元素。此时我们将之前的第一个栈的所有元素重新入栈,并同步更新到第二栈中,就完成了popMax()操作;
代码展示如下:
import java.util.Stack;
class MaxStack {
public static Stack<Integer> xStack;
public static Stack<Integer> maxStack;
public MaxStack() {
xStack = new Stack<Integer>();
maxStack = new Stack<Integer>();
}
public void push(int val) {
xStack.push(val);
int max = maxStack.isEmpty() ? val : maxStack.peek();
maxStack.push(max > val ? max : val);
}
public int pop() {
maxStack.pop();
return xStack.pop();
}
public int top() {
return xStack.peek();
}
public int peekMax() {
return maxStack.peek();
}
public int popMax() {
int max = peekMax();
Stack<Integer> stack = new Stack<Integer>();
while(top() != max){
stack.push(pop());
}
pop();
while(!stack.isEmpty()){
push(stack.pop());
}
return max;
}
}
总结
提示:栈的操作有时需要一个辅助栈,来帮助解决问题。