目录
查找算法
一、顺序查找
二、二分法查找
三、插值查找法
四、斐波那契查找法
查找算法
查找算法根据数据量的大小,可以将其分为以下两种
- 内部查找:内部查找是指在内存或内部存储器中进行查找操作的算法。内部查找适用于数据量较小、存储在内存中或者访问速度较快的情况。常见的内部查找算法有顺序查找、二分法查找、插值查找等。
- 外部查找:外部查找是指在大规模数据集合或存储在外部磁盘等辅助存储介质中进行查找操作的算法。
查找的表格或数据是否变动分为以下两种
- 静态查找:静态查找是指在不改变被查找数据的情况下进行的查找操作。即被查找的表格或数据在查找过程中保持不变。静态查找适用于对静态或只读数据进行查找的场景。一旦建立好索引或者表格,就可以反复进行查找操作而不需要修改数据。常见的静态查找算法有顺序查找、二分法查找、插值查找等。
- 动态查找:动态查找是指在查找过程中可能会修改被查找数据的情况下进行的查找操作。即被查找的表格或数据在查找过程中可能被增加、删除或更新。动态查找适用于对动态数据进行查找的场景,需要实时地对数据变动做出响应。常见的动态查找算法有二叉搜索树、AVL树、红黑树等,这些树结构可以实现高效的查找同时支持动态数据的插入、删除。
一、顺序查找
图解:

算法原理:顺序查找,也称线性查找,是一种基本的查找算法。它逐个地从待查找的元素序列中进行比较,直到找到目标元素或遍历完整个序列为止。具体步骤如下:
- 从序列的第一个元素开始,依次与目标元素进行比较。
- 若当前元素等于目标元素,则查找成功,并返回相应的位置。
- 若当前元素不等于目标元素,则继续下一个元素进行比较。
- 若遍历完整个序列仍未找到目标元素,则查找失败。
案例代码:
public class javaDemo1 {
public static void main(String[] args) {
int data[] = new int[100];
int Target = 99;
int TargetIndex = -1;
Random random = new Random();
for (int i=0;i< data.length;i++){
data[i] = random.nextInt(100);
}
// 循序查找
for (int j=0;j< data.length;j++){
if (data[j] == Target){
TargetIndex = j;
break;
}
}
System.out.println(Arrays.toString(data));
if (TargetIndex!= -1){
System.out.println("找到数据啦,在第"+(TargetIndex+1)+"个数据处");
}else {
System.out.println("抱歉,并没有找到目标数据 喵");
}
}
}
算法总结:顺序查找的时间复杂度为O(n),其中n为待查找序列的长度。由于其简单直观的特点,适用于小规模数据或者无序的数据集合。
二、二分法查找
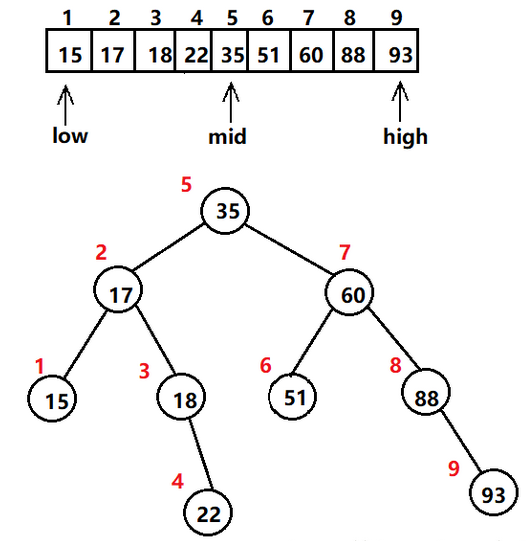
图解:

算法原理:二分法查找,也称折半查找,是一种高效的查找算法,要求待查找的序列必须是有序的。它通过不断缩小查找范围来快速定位目标元素。具体步骤如下:
- 将有序序列的首元素和尾元素分别作为左右边界。
- 计算中间位置mid,取得序列中间的元素。
- 若中间元素等于目标元素,则查找成功,并返回相应的位置。
- 若中间元素大于目标元素,则目标元素可能在左半部分,缩小范围为左边界到mid-1的序列。
- 若中间元素小于目标元素,则目标元素可能在右半部分,缩小范围为mid+1到右边界的序列。
- 重复以上步骤,直到找到目标元素或查找范围为空。
案例代码:
public class javaDemo2 {
public static void main(String[] args) {
int data[] = new int[10];
// 目标值与目标值对应的下角标
int Target = 3;
int TargetIndex = -1;
// 二分法的下界与上界
int low = 0;
int high = data.length-1;
int middle;
Random random = new Random();
for (int i=0;i< data.length;i++){
data[i] = random.nextInt(10);
}
// 形成有序数组
Arrays.sort(data);
// 二分法查找
while (low<=high){
middle = (low+high)/2;
if (data[middle]>Target){
high = middle-1;
}else if (data[middle]<Target){
low = middle + 1;
}else {
TargetIndex = middle;
break;
}
}
System.out.println(Arrays.toString(data));
System.out.println("目标值为"+Target);
if (TargetIndex!= -1){
System.out.println("找到数据啦,在第"+(TargetIndex+1)+"个数据处");
}else {
System.out.println("抱歉,并没有找到目标数据 喵");
}
}
}
算法总结:二分法查找的时间复杂度为O(log n),其中n为待查找序列的长度。由于每次都将查找范围缩小一半,因此效率较高。
三、插值查找法
图解:
算法原理:插值查找法是一种基于二分法的优化查找算法,它在有序序列中根据目标元素的估计位置进行查找,从而提高了查找速度。具体步骤如下:
- 计算目标元素相对于首尾元素的估计位置,即通过公式(target - arr[left]) / (arr[right] - arr[left]) * (right - left) + left 计算出插值位置mid。
- 若插值位置mid超出数组范围,或目标元素小于首元素或大于尾元素,则说明目标元素不存在。
- 若插值位置mid处的元素等于目标元素,则查找成功,并返回相应的位置。
- 若插值位置mid处的元素大于目标元素,则目标元素可能在左半部分,缩小范围为左边界到mid-1的序列。
- 若插值位置mid处的元素小于目标元素,则目标元素可能在右半部分,缩小范围为mid+1到右边界的序列。
- 重复以上步骤,直到找到目标元素或查找范围为空。
案例代码:
public class InsertSerach {
public static void main(String[] args) {
int data[] = new int[10];
int Target = 9;
int TargetIndex = -1;
int low = 0;
int high = data.length-1;
int middle;
Random random = new Random();
for (int i= 0;i< data.length;i++){
data[i] = random.nextInt(10);
}
// 实现数组排列有序
Arrays.sort(data);
// 插入查找
while (low<=high){
middle = low + (high - low) * (Target - data[low]) / (data[high] - data[low]);
if (data[middle]<Target){
low = middle +1;
}else if (data[middle]>Target){
high= middle -1;
}else {
TargetIndex = middle;
break;
}
}
System.out.println(Arrays.toString(data));
if (TargetIndex!= -1){
System.out.println("找到数据啦,在第"+(TargetIndex+1)+"个数据处");
}else {
System.out.println("抱歉,并没有找到目标数据 喵");
}
}
}算法总结:插值查找法的时间复杂度为O(log log n),其中n为待查找序列的长度。它适用于分布均匀的有序序列,但对于分布不均匀的序列效果可能不理想。
四、斐波那契查找法
图解:
算法原理:斐波那契查找法是一种改进的二分查找算法,它利用了黄金分割原理进行查找。首先,需要创建一个斐波那契数列,该数列中的每个元素都是前两个元素之和。
在使用斐波那契查找法时,首先要确定一个斐波那契数列的长度,使得该长度不小于待查找数组的长度。然后,根据斐波那契数列的长度确定两个斐波那契数值——F(k)-1和F(k-2)-1。
接着,在待查找的有序数组中,以F(k)-1位置的元素作为中间值进行比较:
- 若目标值等于中间值,则查找成功,并返回相应的位置。
- 若目标值小于中间值,则在中间值的左半部分继续斐波那契查找。
- 若目标值大于中间值,则在中间值的右半部分继续斐波那契查找。
每次比较后,根据查找范围的缩小情况,选择新的中间值进行下一次的比较,直到找到目标值或者查找范围为空。
案例代码:
public class FibonacciSearch {
public static void main(String[] args) {
int data[] = new int[10];
int Target = 9;
int TargetIndex = -1;
int low = 0;
int high = data.length - 1;
int middle = 0;
Random random = new Random();
for (int i = 0; i < data.length; i++) {
data[i] = random.nextInt(10);
}
Arrays.sort(data);
// 生成斐波那契数列
int[] fibonacci = generateFibonacci(data.length);
// 根据斐波那契数列确定数组长度的最接近值
int length = getClosestFibonacciNumber(data.length);
// 扩展数组长度至斐波那契数列长度
int[] extendedData = Arrays.copyOf(data, length);
for (int i = data.length; i < extendedData.length; i++) {
extendedData[i] = extendedData[data.length - 1];
}
while (low <= high) {
int k = fibonacci[middle - 1];
if (Target < extendedData[middle]) {
high = middle - 1;
middle = low + k - 1;
} else if (Target > extendedData[middle]) {
low = middle + 1;
middle = low + k;
} else {
TargetIndex = Math.min(middle, high);
break;
}
}
System.out.println(Arrays.toString(data));
if (TargetIndex != -1) {
System.out.println("找到数据啦,在第" + (TargetIndex + 1) + "个数据处");
} else {
System.out.println("抱歉,并没有找到目标数据 喵");
}
}
// 生成斐波那契数列
private static int[] generateFibonacci(int length) {
int[] fibonacci = new int[length];
fibonacci[0] = 1;
fibonacci[1] = 1;
for (int i = 2; i < length; i++) {
fibonacci[i] = fibonacci[i - 1] + fibonacci[i - 2];
}
return fibonacci;
}
// 获取斐波那契数列中与数组长度最接近的数值
private static int getClosestFibonacciNumber(int n) {
int a = 0;
int b = 1;
while (b <= n) {
int temp = b;
b = a + b;
a = temp;
}
return a;
}
}
算法总结:斐波那契查找法相比传统二分查找法的优点是,它能够更快地逼近目标值,并且避免了二分查找中取中间值时产生的整数溢出问题。但在某些情况下,斐波那契查找法的性能可能不如二分查找法,因此在实际应用中需要根据具体情况选择合适的查找算法。