文章目录

前言
一、今天学习了什么？
二、关于问题的答案
- 1.牛客网面经
- 2.美团后端一面
- 3.动态规划
总结

前言

提示：这里为每天自己的学习内容心情总结；

Learn By Doing，Now or Never，Writing is organized thinking.

先多，后少。

提示：以下是本篇文章正文内容

一、今天学习了什么？

牛客网的面经；
代码随想录的题目；

二、关于问题的答案

1.牛客网面经

阿里控股集团Java一面（51min）

Q：介绍一下HTTPS的三个具体步骤？

我的理解是应该是讲 HTTPS 的三次握手：

第一步：数字证书认证：

客户端向服务端发送 HTTPS 请求，等待服务器的确认；
服务器将公钥以 数字证书 的形式发送给客户端，保证公钥不被篡改和可信任；
服务端存储了 crt公钥和 crt私钥；
客户端验证证书的有效性；

第二步：获取对称密钥：

客户端用随机数和hash 签名生成一串对称的密钥，使用服务端的公钥对密钥加密；
客户端发送密钥给客户端；
服务端使用私钥解密，获得对称密钥；

第三步：传输加密数据：

服务端使用对称密钥，发送加密的数据；
客户端使用密钥解密和判断数据是否被篡改了；

Q：详细讲一下HTTPS证书验证的过程？

todo

Q：为什么不直接采用RSA，而是采用RSA+对称加密这样的机制？

我的理解是，RSA是一种非对称加密。client 和 server 的通信请求是十分频繁的，而非对称加密虽然对数据的安全性保护好，但是必须考虑到性能。使用非对称加密每次解密是一个很消耗性能和资源的操作，所以为了在安全和性能上达到平衡，使用非对称对通信密钥加密，在真正通信时使用对称加密解密的方式。

Q：线程池主要有哪些参数？

线程池主要有：

核心线程数；
最大线程数；
超时时间；
时间单位；
阻塞队列
线程工厂；
饱和策略；

Q：线程池的工作机制，拒绝策略有哪些，分别对应于哪些情况？

线程池的工作机制：

当一个任务到达线程池时，会判断线程池中的线程数量：
- 如果小于核心线程数，创建一个核心线程去执行任务；
如果核心线程数已满，需要判断阻塞队列是否已满：
- 如果阻塞队列未满，需要直接将任务放入阻塞队列中；
如果阻塞队列已满，需要判断线程池中的线程数和线程池中最大线程数之间的关系：
- 如果线程数小于最大线程数，创建一个救急线程用于执行任务；
如果线程数已经达到了最大线程数，根据指定的饱和策略去执行这个任务；

拒绝策略：

让当前线程暂停原来的任务，去执行这个任务；
丢弃任务，抛出异常；
直接丢弃任务，不抛出异常；
将阻塞队列中等待最久的，也就是下一个要执行的任务丢弃掉，然后将该任务放入阻塞队列中；

Q：面向过程和面向对象的理解？

面向过程，是将解决问题的办法抽象成为方法，每次遇到这种问题就直接调用方法；

面向对象，首先需要抽象成对象，然后将解决问题的办法抽象成对象的方法，解决问题是调用对象的方法。

面向对象更具有扩展性和复用性。

Q：讲一下JVM三个类加载器，Tomcat在类加载的具体流程？

三个类加载分别是：

顶层的 BootstrapClassLoader ，是采用 C 语言编写的，用于加载 JDK 的核心类库
扩展类加载器，用于加载扩展类库；
应用程序类加载器，用于加载应用程序路径下的所有类；

Tomcat 打破了双亲委派机制，首先会去加载 WEB 目录下的类。

Q：如果采用用户自定义的类加载器的话，它会出现什么样的问题？

我的理解是，如果用户重写了 loadClass() 方法，会打破双亲委派模型的机制。

JVM 在判断一个对象是否是同一个对象时，只有被同一个类加载器的同一个类才是相同的。可能存在两个类加载器加载了同一个类，在进行对象比较时，即使是同一个类，但是会被JVM认为是两个类。

Q：JVM有哪些调优的方法？

这个就说一下JVM调优思路和常见工具吧。

JVM 调优思路主要是从内存占用、高吞吐量或低延迟的角度来的。

使用 jps 查看JMV所有的进程状态、jmap 查看堆内存中每个类的实例数量和占用空间，jconsole图形化界面查看JVM各种使用情况。

Q：常见的排序算法，Java的Sort底层是怎么实现的？

冒泡、快排、归并、插入等；

底层是使用双轴快速排序实现的。

Q：详细讲一下快速排序当中具体怎么比较每个元素的（左右指针）？

有一个基准值，首先比较左指针的元素和基准值的大小：

小于基准值，就向右移动左指针；
大于等于基准值，就跳出循环；

然后比较右指针元素和基准值的大小：

大于基准值，就向左移动右指针；
小于基准值，就跳出循环；

此时，交换一次做右指针的元素，移动左右指针，然后重复上述操作，直至指针碰撞；

进行到这里时，一次快排完成，然后分别去左部分和右部分进行快排；

Q：Spring当中的Bean的作用域有哪些？

有singleton、prototype、request、session、application等；

Spring 中 Bean 的作用域通常有下面几种：

singleton :
- IoC 容器中只有唯一的 bean 实例；
- Spring 中的 bean 默认都是单例的，是对单例设计模式的应用。
prototype :
- 每次获取都会创建一个新的 bean 实例；
- 连续 getBean() 两次，得到的是不同的 bean 实例。
request :
- 请求 bean ；
- 仅 Web 应用可用；
- 每一次 HTTP 请求都会产生一个新的 bean，该 bean 仅在当前 HTTP request 内有效。
session :
- 仅 Web 应用可用；
- 会话 bean ；
- 每一次来自新 session 的都会产生一个新的 bean，该 bean 仅在当前 HTTP session 内有效。
application/global-session ：
- 仅 Web 应用可用；
- 应用 Bean ；
- 每个 Web 应用在启动时创建一个 Bean，该 bean 仅在当前应用启动时间内有效。
websocket ：
- 仅 Web 应用可用；
- 每一次 WebSocket 会话产生一个新的 bean。

Q：Springboot的启动流程？

启动一个 SpringBoot 工程，大概分为两步。

通过构造函数，创建一个 SpingApplication 实例：
- 会将，资源加载器（resourceLoader）和主方法类（primarySources）加载到主内存中；
- 确定 WEB 服务类型，默认是 servlet ，还有 NONE 、 REACTIVE ；
- 读取 META-INF/spring.factories 的配置类，进行装配；
- 定位 main 方法所在的类，就是启动类本身；
执行 SpringApplication.run() 方法：
- 构建计时器，用于记录 SpringBoot 的启动时间；
- 初始化监听器，并启动监听，用于监听 run() 方法的执行；
- 初始化环境；
- 打印 banner 和版本；
- 构造 Spring 容器，填充容器（环境、配置），初始化容器；
- 监听器监听到启动容器完成，计时器停止计时，打印启动时长；
- 监听器继续监听正在运行的容器；

Q：介绍一下ApplicationContext？

ApplicationContext 是 Spring 应用程序上下文，相当于是一个容器，负责创建、获取、管理 bean 。

是高级版本的 BeanFactory ，具有更多的功能，具有事件机制、解析消息支持国际化的能力等。

public interface ApplicationContext extends EnvironmentCapable, ListableBeanFactory, HierarchicalBeanFactory,
      MessageSource, ApplicationEventPublisher, ResourcePatternResolver {}

最重要的区别是：

BeanFactory 采用的是延迟加载，只有当需要使用到某个 bean 对象时，才会进行加载实例化。这个样子的缺点是，不能及时发现 Spring 的配置问题，如果 bean 的某一个属性没有注入，只有第一次调用 getBean() 时才会抛出异常。

而 ApplicationContext 是在加载时，就一次性创建了所有的 bean ，有利于检查依赖属性是否注入。在使用 bean 时，无需等待创建，直接拿取就可以使用。缺点就是，占用内存空间，应用程序配置的 bean 很多时，启动会比较慢。

并且 BeanFactory 通常以编程的方式被创建，而 ApplicationContext 是声明的方式去创建。

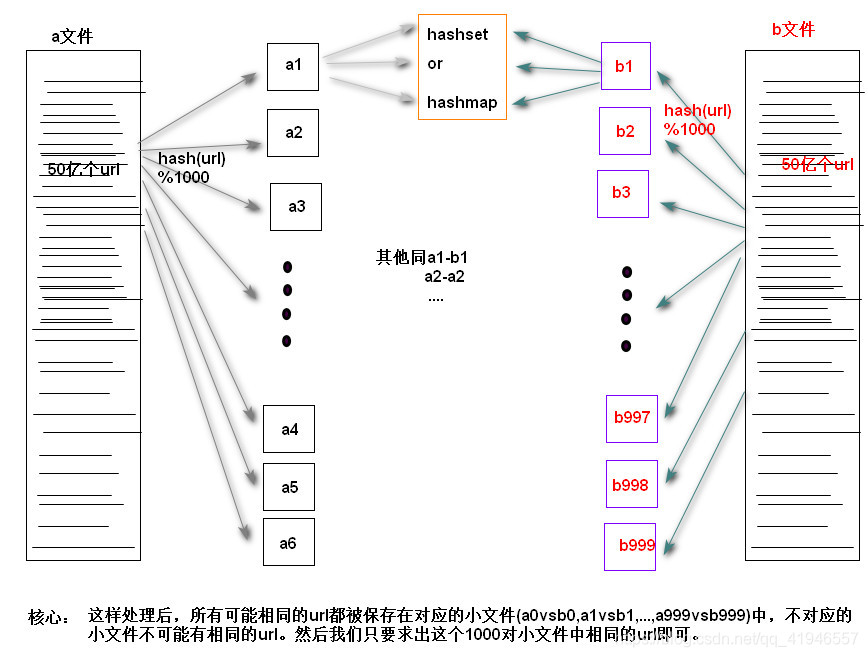
Q：有 A,B 两个文件（50亿个URL）每个URL具有64B的大小，4GB内存，怎么找到这两个文件所含有的公共URL？

也可以采用布隆过滤器，但是我个人认为不太好。

采用分治的思想：

利用一个 hash 函数，分别遍历 A，B 文件中的所有数据，将其拆分成小文件进行存储；
遍历 A 中的小文件，利用一个 hashSet 存储，然后同样遍历 B 小文件判断是否存在 Set 中存在该元素，如果是则表明是相同的 url ，进行存储即可。

2.美团后端一面

美团后端一面

Q：反射的理解，应用举例？

todo

Q：ThreadLocal原理，项目中用到了，又结合起来问了一些场景?

todo

Q：线程池核心参数?

todo

Q：丢弃策略一般使用什么比较好?

todo

Q：mysql索引，事务等等，说你知道的?

todo

Q：如何考虑索引效率问题，比如命中，索引大小，合理性问题等等?

todo

3.动态规划

300. 最长递增子序列（⭐⭐⭐）

    public int lengthOfLIS(int[] nums) {
        /**
         * 最长递增子序列的长度，严格递增
         * dp[i]，代表数组下标从[0，i]的最长递增子序列的长度
         * 每个元素的最长递增子序列的长度，最少为1
         */
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int res = 0;

        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                // 只有当nums[i] > nums[j] 时，才需要判断
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            res = Math.max(res, dp[i]);
        }

        return res;
    }

674. 最长连续递增序列（⭐⭐⭐⭐⭐）

    public int findLengthOfLCIS(int[] nums) {
        /**
         * 最长且连续递增的子序列，要求该序列中的每个元素都是递增的
         * dp[i]代表以元素下标i结尾时，最长且连续递增的子序列的长度
         */
        int length = nums.length;
        int res = 1;
        int[] dp = new int[length];
        dp[0] = 1;

        for (int i = 1; i < length; i++) {
            // 只有当当前元素大于前一个元素时，才计算
            if (nums[i] > nums[i - 1]) {
                dp[i] = dp[i - 1] + 1;
            } else {
                dp[i] = 1;
            }
            res = Math.max(dp[i], res);
        }

        return res;
    }

718. 最长重复子数组（⭐⭐⭐⭐⭐）

    public int findLength(int[] nums1, int[] nums2) {
        /**
         * 最长重复子数组：
         *  返回两个数组中 公共的、长度最长的子数组的长度
         *  dp[i][j]代表nums1[0,i-1]结尾和nums2[0,j-1]结尾的公共的、长度最长的子数组的长度
         */
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        int res = 0;

        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > res) {
                    res = dp[i][j];
                }
            }
        }

        return res;
    }

1143. 最长公共子序列

    public int longestCommonSubsequence(String text1, String text2) {
        /**
         * 一个字符串的子序列，可以删除某些字符，只需要保证相对顺序不变
         * dp[i][j]，表示text1下标末尾为[0,i-1]和text2下标为[0,j-1]的最长公共子序列
         */
        int m = text1.length();
        int n = text2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    // 如果两个字符相等
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    // 由于字符可以维持相对顺序，删除，所以不等的情况下，逻辑是这个样子的
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[m][n];

    }

1035. 不相交的线（⭐⭐⭐⭐⭐）- 第一眼毫无思路

    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        /**
         * 泪目了
         * 看似是求两个数组中的最大连接线数，其实是求两个数组的最长公共子序列
         */
        int m = nums1.length;
        int n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[m][n];

    }

53. 最大子数组和

    public int maxSubArray(int[] nums) {
        /**
         * dp[i] ，是以数组下标为 i 结尾的最大和
         */
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = nums[0];

        for (int i = 1; i < nums.length; i++) {
            // 判断当前值和之前的大小
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            res = dp[i] > res ? dp[i] : res;
        }

        return res;
    }

392. 判断子序列（⭐⭐⭐⭐⭐）- 这个真的有点难，注意画图推导

    public boolean isSubsequence(String s, String t) {
        /**
         * dp[i][j] 是以 i-1 结尾的s，是否是 j-1 结尾的子序列
         */
        int m = s.length();
        int n = t.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }

        return dp[m][n] == s.length();
    }

583. 两个字符串的删除操作

    public int minDistance(String word1, String word2) {
        /**
         * 我的思路是，找到word1和word2的最长子序列的长度
         */
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        int length = dp[m][n];
        return word1.length() + word2.length() - 2 * length;
    }

115. 不同的子序列

    public int numDistinct(String s, String t) {
        /**
         * dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
         */
        int m = s.length();
        int n = t.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            dp[i][0] = 1;
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }

        return dp[m][n];
    }