01背包问题（二维）

视频讲解：带你学透0-1背包问题！| 关于背包问题，你不清楚的地方，这里都讲了！| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili

01背包问题（一维、滚动数组）

视频讲解：带你学透01背包问题（滚动数组篇） | 从此对背包问题不再迷茫！_哔哩哔哩_bilibili

leetcode 416. 分割等和子集

题目链接：416. 分割等和子集 - 力扣（LeetCode）

视频链接：动态规划之背包问题，这个包能装满吗？| LeetCode：416.分割等和子集_哔哩哔哩_bilibili

题目概述

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

思路

可以把本题当成01背包问题，本题可以这样去想：把集合里所给的每个元素当成一个物品，每个元素不能重复使用，每个元素的数值既是重量也是价值，背包容量为target，如果dp[target]==target，说明背包装满。

依旧是动规五部曲：

1.确定dp数组以及下标的含义

dp[j]表示：背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。

2.确定递推公式

递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])

3.dp数组初始化

dp[0]==0，如果题中所给的都是正整数的话，剩下的都初始化为0就好了，如果有负数，就初始化为负无穷。

4.确定遍历顺序

第一层for循环是遍历物品，第二层for循环是遍历背包（并且是倒序遍历）。

5.打印dp数组

 

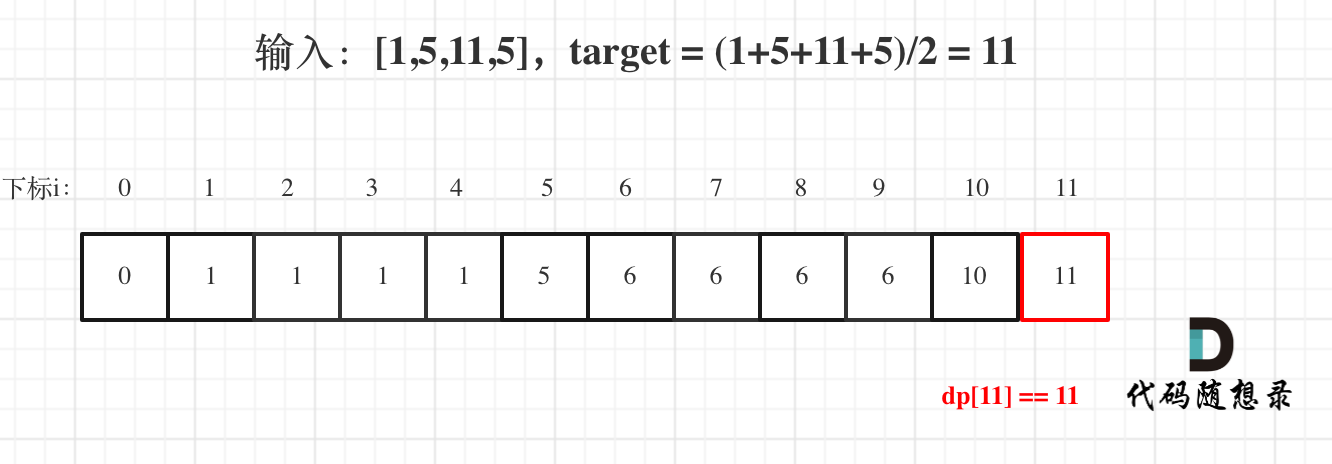
代码实现

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        vector<int> dp(10001,0);
        for(int i = 0;i < nums.size();i++) {
            sum += nums[i];
        }
        if(sum % 2 == 1) return false;
        int target = sum / 2;
        for(int i = 0;i < nums.size();i++) {
            for(int j = target;j >= nums[i];j--) {
                dp[j] = max(dp[j],dp[j - nums[i]] + nums[i]);
            }
        }
        if(dp[target] == target) return true;
        return false;

    }
};