2023/8/27周报

摘要

论文阅读

1、标题和现存问题

2、过度平滑和度量方法

3、处理过坡

4、实验结果

深度学习

1、解决可视化问题

2、CART算法

总结

摘要

本周在论文阅读上，阅读了一篇Pairnorm:解决GNNS中的过平滑问题的论文。PairNorm 的核心思想是在图卷积层之间引入节点对之间的特征差异。它通过在图卷积层的输出上引入额外的正则化项，来鼓励节点对之间的特征差异。具体来说，PairNorm 会对同一图卷积层的不同节点对之间的特征进行归一化，使得每对节点的特征差异保持一定的距离。这篇论文通过引入 PairNorm 正则化方法，成功地解决了图神经网络中的过度平滑问题，提升了模型的表示能力和性能。在深度学习上，解决了上周遗留下来的可视化问题和再次学习了CART算法。

This week, in terms of paper reading, reviewing a paper titled "PairNorm: Mitigating Over-Smoothing in Graph Neural Networks." The core idea of PairNorm is to introduce feature differences between node pairs in between graph convolutional layers. It achieves this by adding an additional regularization term to the outputs of graph convolutional layers to encourage feature disparities among node pairs. Specifically, PairNorm normalizes the features between different node pairs within the same graph convolutional layer, ensuring a certain distance in feature differences between each pair of nodes. By introducing the PairNorm regularization method, this paper successfully addresses the issue of over-smoothing in graph neural networks, thereby enhancing the model's representation capacity and performance. In terms of deep learning, tackling the visualization problem left from last week and revisited the CART algorithm.

论文阅读

1、标题和现存问题

标题：Pairnorm:解决GNNS中的过平滑问题

现存问题：gnn的一个关键问题是其深度限制。据观察，深度叠加层通常会导致 gnn(如GCN和GAT)的性能显著下降，甚至超过几个(2-4)层。这种下降与许多因素有关;包括反向传播中逐渐消失的梯度，由于参数数量的增加而出现的过拟合，以及称为过平滑的现象。图卷积是一种拉普拉斯平滑，并证明了在多次使用拉普拉斯平滑后，(连通的)图中节点的特征会收敛到相似的值——这个问题被称为“过平滑”。实际上，过度平滑会导致不同类之间的节点表示难以区分，从而影响分类性能。

2、过度平滑和度量方法

过度平滑指的是在多层图神经网络中，节点特征在不同层之间逐渐趋于相似，失去了节点之间的差异性，导致模型在节点分类和预测任务中的性能下降。

过度平滑现象的原因。主要观点包括：

线性层的传播效应：在多层图神经网络中，由于每一层的信息传递都是基于前一层的线性组合，信息传递会逐渐减弱，导致节点特征在不同层之间趋于一致。
信息聚合的稀疏性：随着层数增加，节点特征的信息会通过多次的聚合传递，使得节点之间的差异性逐渐减少，最终导致节点特征过于平滑。
初始特征的影响：节点初始特征在多层传播中会逐渐被稀释，如果初始特征差异性较小，经过多层传播后差异性会进一步减小，导致过度平滑。

文章提出的度量方法旨在衡量图神经网络（GNNs）中节点特征的平滑程度，以帮助检测和分析过度平滑的现象。这种度量方法有助于理解模型在不同层之间特征的变化情况，进而评估模型对节点之间差异性的保持能力。

通过衡量节点特征的平滑程度，可以识别出在多层GNN中是否存在过度平滑的问题。如果节点特征在不同层之间过于趋同，失去了差异性，那么就可能存在过度平滑，这可能导致模型性能下降。通过度量节点特征的平滑程度，研究者可以更好地理解模型的行为，并在设计和调整模型时采取相应的措施来缓解过度平滑问题。

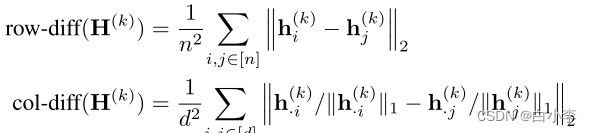
row-diff测度是节点特征(即表示矩阵的行)之间所有两两距离的平均值，量化了节点的超平滑，而col-diff是(L1-归一化 1)列，并量化特征超平滑。

SGC通过将多层GCN中的复杂卷积操作简化为邻接矩阵的幂操作，实现了特征的传播和聚合。这种简化的操作降低了模型的复杂性，同时减少了超平滑的影响。SGC通过只使用一层卷积，将邻接矩阵的幂函数作为卷积核，从而避免了多层卷积导致的过度平滑问题。

因此，SGC研究超平滑的目的是通过简化模型结构和操作，减轻多层GCN中的超平滑问题，从而提高模型的表现和泛化能力。

3、处理过坡

建立了图卷积和一个优化问题之间的联系，即图正则化最小二乘：

上面公式中的优化问题有助于更深入地研究图卷积的过平滑问题。理想情况下，希望在相同的集群中获得平滑，但是避免平滑来自不同集群的节点。上面公式中的目标通过图形正则化项只规定了第一个目标。因此，当反复使用卷积时，它容易出现过平滑。为了解决这个问题并同时实现这两个目标，我们可以添加一个负数项，例如断开连接的对之间的距离之和，如下所示。

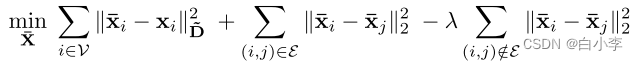
这里 λ是一个平衡标量，以考虑两个目标的不同体积和重要性。在文章中，我们采取了不同的路线。我们提出了一种通用而有效的“补丁”，称为 PAIRNORM，而不是一个全新的图卷积算子，它可以应用于任何形式的有过平滑潜力的图卷积。

提出的PAIRNORM(带有输入~ X和输出X˙)可以被写成一个两步、中心和规模的归一化过程:

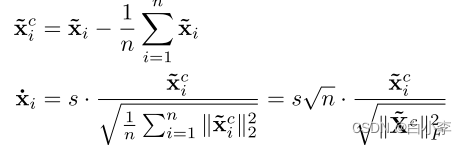
PAIRNORM的说明，包括定心和缩放步骤：

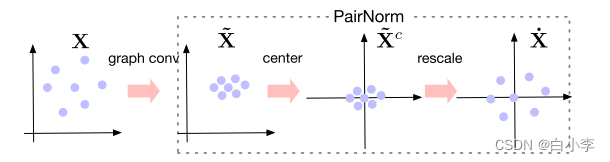
原始与pairnorm增强GCN和GAT模型在Cora上层数增加的性能比较。

如果任务需要大量的层来实现其最佳性能，那么更多地使用 PAIRNORM会使任务受益。为此，研究了“缺失特征设置”，即节点的子集缺少特征向量。将该任务的这种变体称为缺失向量的半监督节点分类(SSNC-MV)。

下图展示了SGC、GCN和GAT模型在Cora 上随层数增加的性能，其中我们从所有未标记的节点中去除特征向量，即 p = 1。与那些没有 PAIRNORM的模型相比，使用 PAIRNORM的模型获得了更高的测试精度，它们通常可以达到更多的层。

4、实验结果

数据集：Cora、Citeseer、Pubmed、Coauthor。

将 PAIRNORM应用于SGC对SSNC-MV的全局性能增益。pairnormn 增强的SGC在缺失0%以上的情况下表现类似或更好，而在大多数其他设置下，特别是在缺失率较大的情况下，它的表现明显优于普通 SGC。

对相同设置下的GCN和GAT采用PAIRNORM-SI，并将其与剩余(跳过)连接技术进行比较。

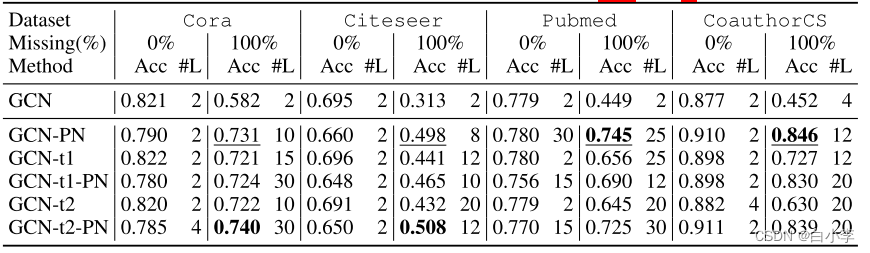
GCN和GAT模型表现出相似的趋势:

(1)在 SSNC-MV 条件下，随着缺失率的增加，香草模型的性能下降;

(2)剩余连接和PAIRNORM-SI 都能使模型更深入，并提高性能；

(3) GCN-PN和GAT-PN实现的性能是可比的或比仅仅使用跳跃;

(4)通过使用跳跃和PAIRNORM-SI 可以进一步提高性能(尽管是轻微的)。

PAIRNORM计算速度快，不需要改变网络结构，也不需要任何额外的参数，可以应用于任何GNN。在真实的分类任务上的实验表明了 PAIRNORM的有效性，当任务受益于更多的层时，它提供了性能提升。

深度学习

1、解决可视化问题

导入必要的库：
- 代码开始时导入了所需的库，如pandas、pyecharts和os。
读取数据：
- 代码使用pd.read_excel从Excel文件读取数据。数据似乎以年份为行，城市为列的形式组织。
创建时间轴和地图图表：
- 代码使用Timeline(init_opts=opts.InitOpts(...))初始化时间轴。这为时间轴设置了一些初始选项，如宽度、高度、主题和页面标题。
- 然后，它遍历数据中的每个年份，并为每个年份创建地图图表。对于每个年份：
  - 从DataFrame中获取该年份的CO数据作为一行。
  - 将城市名称与其相应的CO浓度级别结合起来。
  - 使用pyecharts库创建一个Map图表，并将数据添加到其中。
  - 设置各种图表选项，包括标题和CO浓度级别到颜色的可视映射。
将地图添加到时间轴：
- 在循环内，它使用timeline.add()方法将每个地图图表添加到时间轴，指定图表和相应的时间点（年份）。
时间轴配置：
- 在添加所有地图图表到时间轴后，它使用timeline.add_schema()配置时间轴设置。这启用了自动播放，并设置了帧之间的播放间隔。
渲染时间轴：
- 使用timeline.render()将时间轴渲染为HTML文件。
- 使用os.system()命令在默认的网络浏览器中打开生成的HTML文件。

import pandas as pd
from pyecharts.charts import Map
from pyecharts import options as opts
from pyecharts.charts import Timeline
import os
if __name__ == '__main__':
    # 读取数据
    data = pd.read_excel('./显示结果表/真实结果单独表（前15行）/CO_表(真实).xlsx', index_col=0)
    years = data.index.tolist()
    cities = data.columns.tolist()
    # 创建地图示例
    map_chart = Map()
    timeline = Timeline(init_opts=opts.InitOpts(
            width='1300px',
            height='830px',
            theme="广西CO变化",
            page_title="广西CO变化",
    ))

    for k, year in enumerate(years):
        row = data.iloc[k,].tolist()
        economic_data = list(zip(cities, row))
        map = (Map().add(year, economic_data, "广西").set_global_opts(
            title_opts=opts.TitleOpts(title="广西CO变化(2020年)_真实"), visualmap_opts=opts.VisualMapOpts(
                                              # max_=1,
                                              # range_color=["#FFFFFF", "#FFCC00", "#CC0000"],  # 这里修改颜色，低、中、高
                                              pieces=[{'min': 0.3980778753757477, 'max': 0.5579649806022644, 'label': "0.39-0.55", 'color': '#9ecae1'},
                                                      {'min': 0.5581204891204834, 'max':   0.6000000238418579, 'label':"0.55-0.60" , 'color': '#6baed6'},
                                                      {'min':0.6000000238418579, 'max':  0.643344521522522, 'label': "0.60-0.64", 'color': '#4292c6'},
                                                      {'min': 0.647230863571167, 'max':  0.699999988079071, 'label': "0.64-0.69", 'color': '#2171b5'},
                                                      {'min': 0.699999988079071, 'max': 0.800000011920929, 'label': "0.69-0.80", 'color': '#08519c'},
                                                      {'min':0.800000011920929, 'max': 0.8999999761581421, 'label': "0.80-0.89",
                                                       'color': '#ffaaaa'},
                                                      {'min': 0.8999999761581421, 'max':  1.277964234352112, 'label': "0.89-1.28",
                                                       'color': '#e64b50'},
                                                      ],
                                              is_piecewise=True,
                                              pos_bottom="10%", pos_left="25%",
                                              ))
        )
        print(f"Adding map for year: {year}")
        timeline.add(chart=map, time_point=year)
    timeline.add_schema(is_auto_play=True, play_interval=500)


    timeline.render("./html/真实html/Reality_CO.html")
    os.system("html/真实html/Reality_CO.html")

2、CART算法

CART（Classification and Regression Trees，分类与回归树）算法是一种常用的决策树算法，用于解决分类和回归问题。CART算法通过递归地将数据集分割成子集，并在每个子集上构建最佳拟合的树结构。在分类问题中，每个叶节点代表一个类别，而在回归问题中，每个叶节点代表一个数值。

CART算法的基本原理：

树的构建： 算法从根节点开始，选择一个特征和一个阈值，将数据集分成两个子集。该过程是通过选择一个特征和一个切分点，将数据集分为两部分，以最小化切分后的子集的不纯性度量（如Gini指数、熵等）。
递归分割： 每个子集都被递归地继续切分，直到满足终止条件。终止条件可以是达到指定的最大深度、数据集的大小小于某个阈值，或子集的不纯性达到一定程度。
叶节点： 一旦停止分割，每个子集被赋予一个叶节点，并用于表示一个类别（在分类问题中）或一个数值（在回归问题中）。
剪枝： 构建好的树可能存在过拟合的问题，因此需要进行剪枝操作。剪枝是通过移除一些节点和子树，来减少模型的复杂度，以提高泛化能力。
预测： 使用构建好的决策树对新数据进行预测。从根节点开始，根据特征值的判定条件，沿着树的分支向下移动，最终到达叶节点，该叶节点的值即为预测结果。

CART算法在分类问题中可以使用基尼指数（Gini index）或熵（Entropy）来衡量不纯性，从而选择最佳的特征和切分点。在回归问题中，通常使用均方误差（Mean Squared Error，MSE）来度量拟合程度。

import numpy as np

# 定义一个决策树节点类
class DecisionNode:
    def __init__(self, feature_index=None, threshold=None, value=None, left=None, right=None):
        self.feature_index = feature_index   # 特征索引
        self.threshold = threshold           # 切分阈值
        self.value = value                   # 叶节点值（类别）
        self.left = left                     # 左子树
        self.right = right                   # 右子树

# 定义一个CART分类器类
class CARTClassifier:
    def __init__(self, max_depth=None):
        self.max_depth = max_depth

    # 计算基尼不纯度
    def gini(self, y):
        unique_labels, counts = np.unique(y, return_counts=True)
        p = counts / len(y)
        gini_score = 1 - np.sum(p ** 2)
        return gini_score

    # 根据特征和阈值切分数据集
    def split(self, X, y, feature_index, threshold):
        left_mask = X[:, feature_index] <= threshold
        right_mask = ~left_mask
        left_X, left_y = X[left_mask], y[left_mask]
        right_X, right_y = X[right_mask], y[right_mask]
        return left_X, left_y, right_X, right_y

    # 找到最佳切分特征和阈值
    def find_best_split(self, X, y):
        m, n = X.shape
        best_gini = float('inf')
        best_feature = None
        best_threshold = None

        for feature_index in range(n):
            thresholds = np.unique(X[:, feature_index])
            for threshold in thresholds:
                left_X, left_y, right_X, right_y = self.split(X, y, feature_index, threshold)
                gini_left = self.gini(left_y)
                gini_right = self.gini(right_y)
                gini_score = (len(left_y) / m) * gini_left + (len(right_y) / m) * gini_right

                if gini_score < best_gini:
                    best_gini = gini_score
                    best_feature = feature_index
                    best_threshold = threshold

        return best_feature, best_threshold

    # 递归地构建决策树
    def build_tree(self, X, y, depth=0):
        if depth >= self.max_depth:
            value = np.argmax(np.bincount(y))
            return DecisionNode(value=value)

        best_feature, best_threshold = self.find_best_split(X, y)
        if best_feature is None:
            value = np.argmax(np.bincount(y))
            return DecisionNode(value=value)

        left_X, left_y, right_X, right_y = self.split(X, y, best_feature, best_threshold)
        left_subtree = self.build_tree(left_X, left_y, depth + 1)
        right_subtree = self.build_tree(right_X, right_y, depth + 1)

        return DecisionNode(feature_index=best_feature, threshold=best_threshold,
                            left=left_subtree, right=right_subtree)

    # 训练模型
    def fit(self, X, y):
        self.tree = self.build_tree(X, y)

    # 预测单个样本
    def predict_one(self, node, x):
        if node.value is not None:
            return node.value
        if x[node.feature_index] <= node.threshold:
            return self.predict_one(node.left, x)
        else:
            return self.predict_one(node.right, x)

    # 预测多个样本
    def predict(self, X):
        predictions = [self.predict_one(self.tree, x) for x in X]
        return np.array(predictions)

# 生成一些随机数据用于演示
np.random.seed(0)
X = np.random.rand(100, 2)
y = (X[:, 0] + X[:, 1] > 1).astype(int)

# 创建CART分类器实例并训练
cart_classifier = CARTClassifier(max_depth=3)
cart_classifier.fit(X, y)

# 预测并输出结果
test_data = np.array([[0.2, 0.8], [0.8, 0.2]])
predictions = cart_classifier.predict(test_data)
print("Predictions:", predictions)