原视频:https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili:Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili
Houdini版本:19.5
1、概述
递归是一种直接或者间接地调用自身的算法,一般计算机中的递归算法实现不适用于Houdini的Vex(通过函数或子过程来完成)。详情可见后面谢尔宾斯基三角的例子。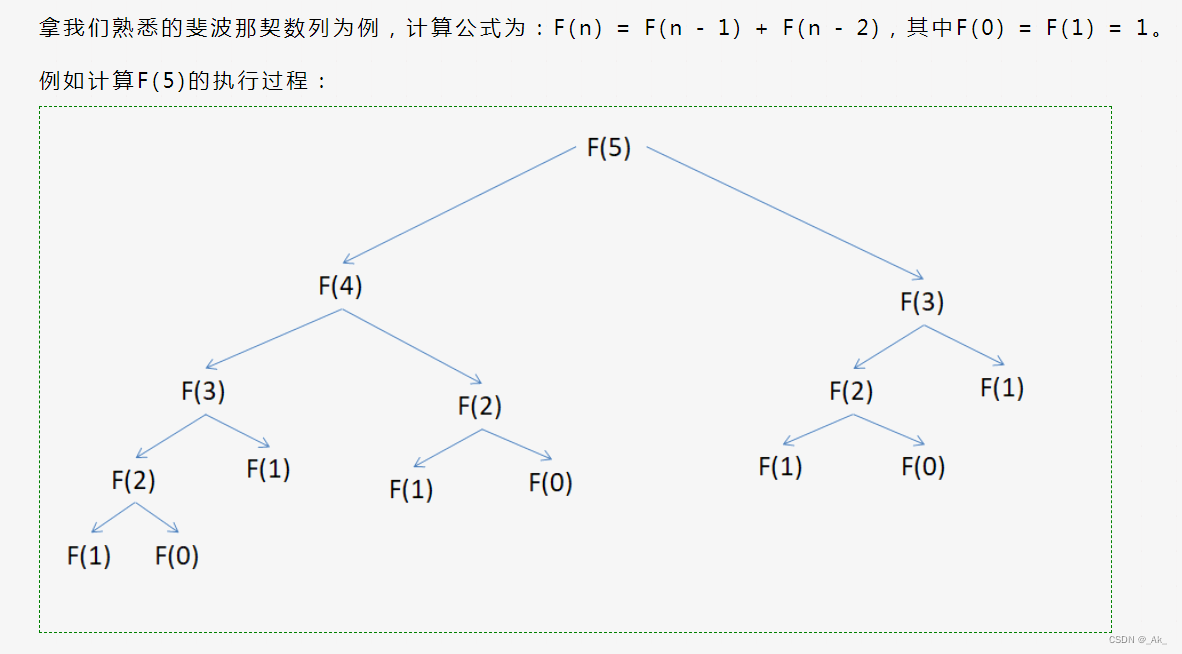
图片来自@bky2016的文章,感兴趣可以去看看。
本章主要使用以下几种方式实现递归:
A)、For-Each节点,
B)、For-Each节点 + VEX,
C)、Solver解算器,
D)、纯VEX(复杂),
提前剧透:B、C两种方法计算最快,
关于For-each节点,可以看这知乎@ZeTii的Houdini 中for-each 和for-loop 节点文章。
2、螺旋线与回归
用上面的四种方法分别实现一根螺旋线,
①节点连接及设置如下,(代码节点的通道值自行设置),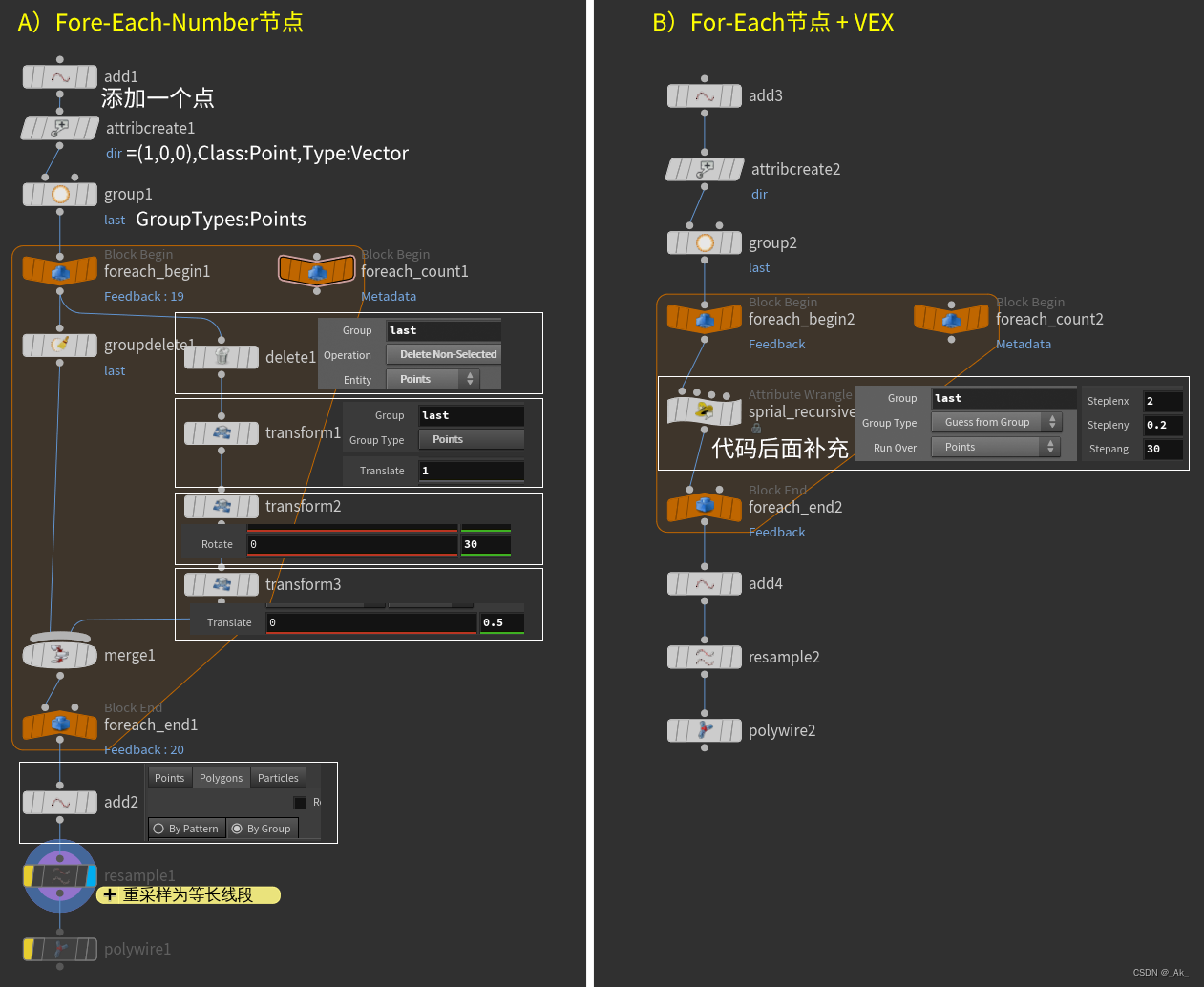
②补充,节点代码如下,
// B——sprial_recursively节点代码
float steplenx = chf('steplenx');
float stepleny = chf('stepleny');
float stepang = chf('stepang');
vector pos = @P;
pos = pos + v@dir * steplenx; // pos沿X位移
matrix mat = ident();
rotate(mat, radians(stepang), set(0,1,0));
pos *= mat;
pos += set(0,1,0) * stepleny; // pos沿Y位移,即高度
int newpoint = addpoint(0, pos);
setpointattrib(0, 'dir', newpoint, v@dir);
//盲猜在For-Each循环内,除了第一次,其它循环不能访问外部属性
setpointgroup(0, 'last', newpoint, 1);
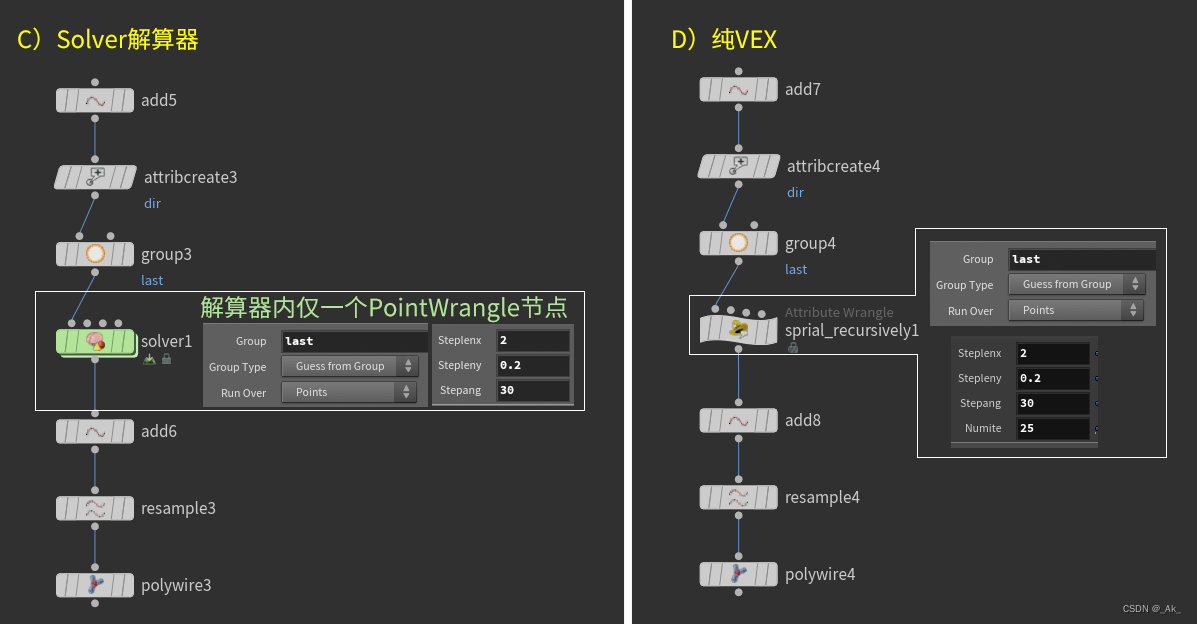
setpointgroup(0, 'last', @ptnum, 0);// C——解算器Solver内代码
//与上面一样// D——sprial_recursively1节点代码
vector pos = @P;
for(int i=0; i<chi('numite'); i++){
float steplenx = chf('steplenx');
float stepleny = chf('stepleny');
float stepang = chf('stepang');
pos = pos + v@dir * steplenx; // pos沿X位移
matrix mat = ident();
rotate(mat, radians(stepang), set(0,1,0));
pos *= mat;
pos += set(0,10) * stepleny; // pos沿Y位移,即高度
int newpoint = addpoint(0, pos);
//属性设置不用啦,可以直接访问了
}3、谢尔宾斯基三角与递归
谢尔宾斯基三角形是这样子的,
本节主要用下面的方法实现谢尔宾斯基三角,(当然,也有其它方法),
For-Each实现方法,
其它三种实现原理大概如下,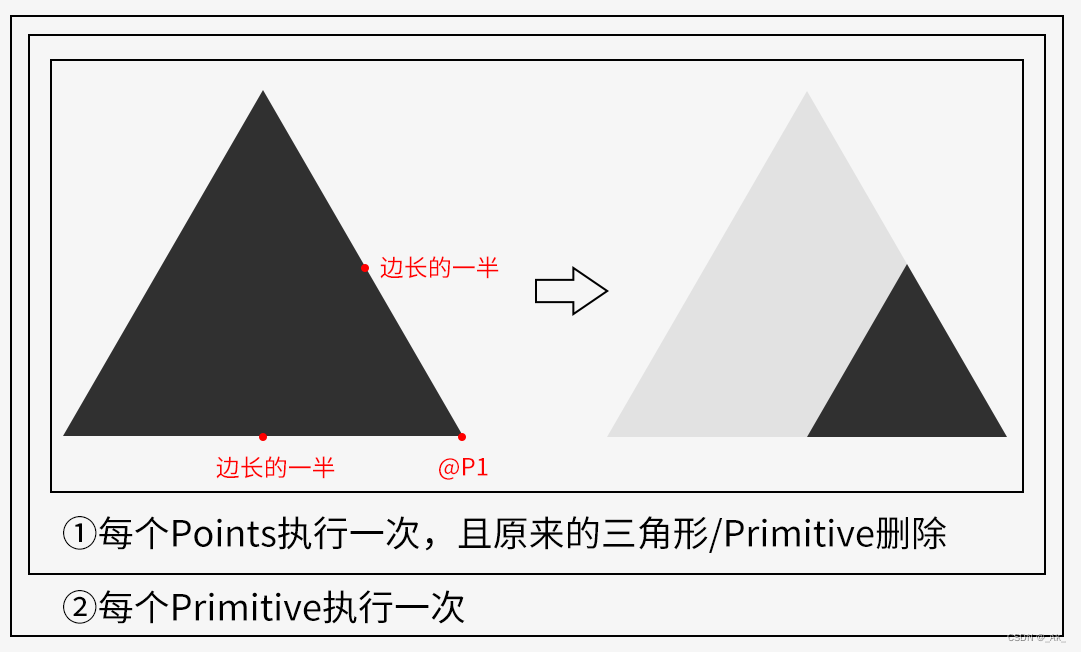
①节点连接及设置如下,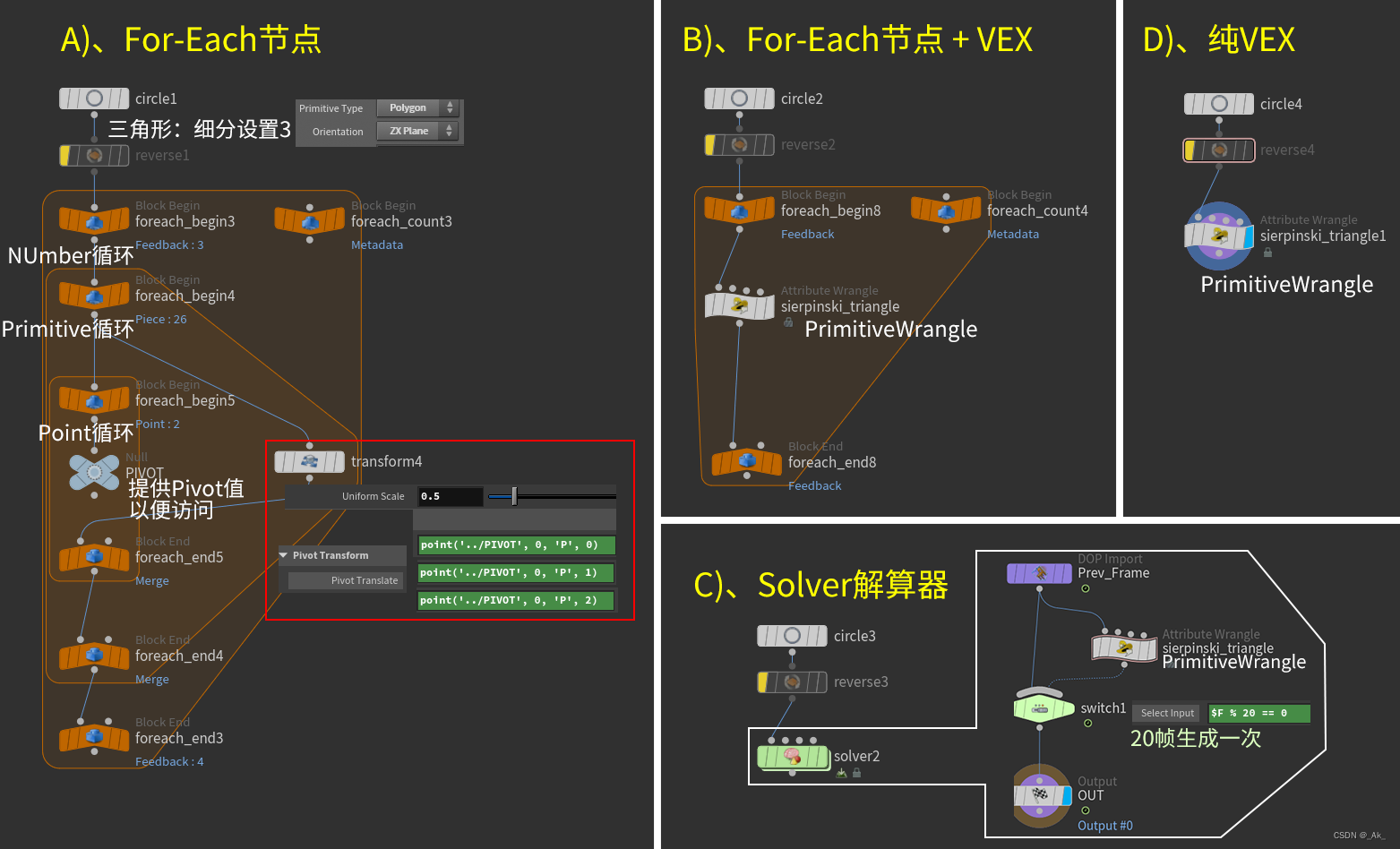
②补充,节点代码如下,
// B——sierpinski_triangle节点代码
int pts[] = primpoints(0, @primnum);
for(int i=0; i<len(pts); i++){
int pt = pts[i];
vector pos = point(0, 'P', pt);
int triprim = addprim(0, 'poly');
for(int n=0; n<len(pts); n++){
int npt = pts[n];
vector npos = point(0, 'P', npt);
npos -= pos;
npos *= 0.5;
npos += pos;
int newpoint = addpoint(0, npos);
addvertex(0, triprim, newpoint);
}
}
removeprim(0, @primnum, 1);// C——解算器Solver内代码
//与上面一样// D——sierpinski_triangle1节点内代码
int pts[] = primpoints(0, @primnum);
vector positions[] = array();
for(int i=0; i<len(pts); i++){
vector pos = point(0, 'P', pts[i]);
append(positions, pos);
}
for(int t=0; t<chi('numite'); t++){
int numtri = len(positions) / 3;
vector newpositions[] = array();
for(int s=0; s<numtri; s++){
for(int i=0; i<3; i++){
vector pos = positions[s * 3 + i];
for(int n=0; n<3; n++){
vector npos = positions[s * 3 + n];
npos -= pos;
npos *= 0.5;
npos += pos;
append(newpositions, npos);
}
}
}
positions = newpositions;
}
removeprim(0, @primnum, 1);
int numtri = len(positions) / 3;
for(int s=0; s<numtri; s++){
int tri = addprim(0, 'poly');
for(int i=0; i<3; i++){
vector pos = positions[s * 3 + i];
int npt = addpoint(0, pos);
addvertex(0, tri, npt);
}
}4、性能测试:谢尔宾斯基三角
性能测试点这里,不懂去看视频(1h45min)。
结果: 谢尔宾斯基三角11次迭代花费时间,
5、2D L-系统树与递归
分叉分形,为下一节的3D树打基础,老规矩先上结果,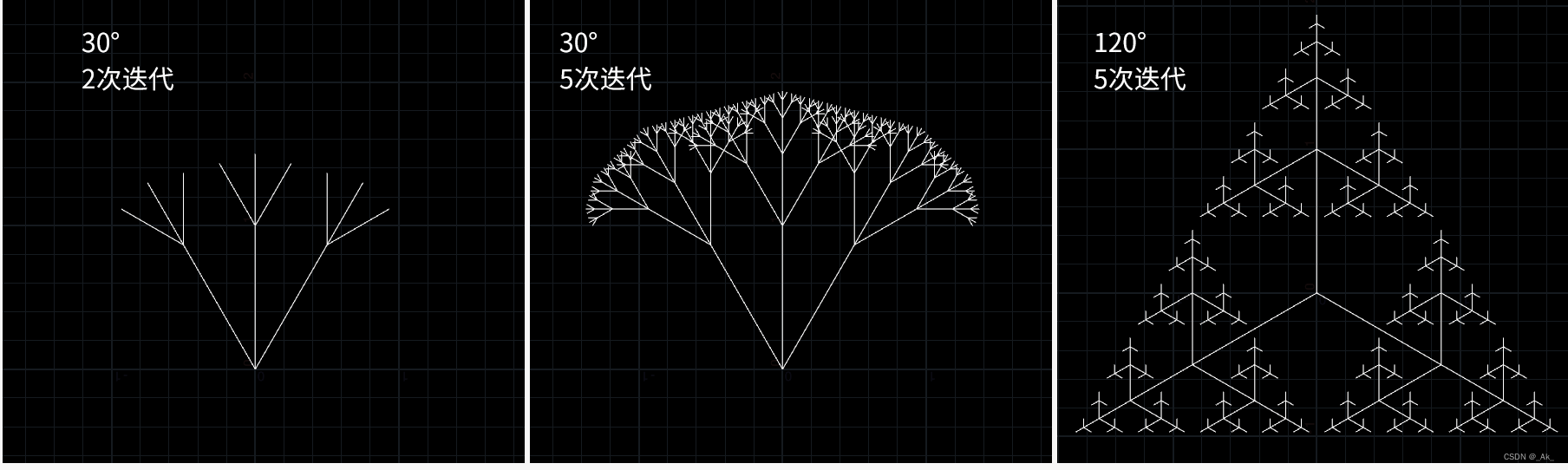
eg.①节点设置及连接如下, 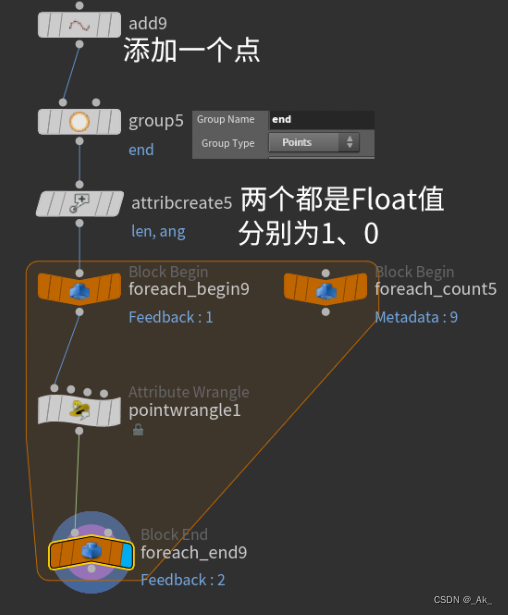
②补充,pointwrangle1节点代码如下,
float branchang = radians(chf('branchang')); //范围设 0~120
for(int i=0; i<3; i++){
float a = -branchang + i * branchang + f@ang; //妙鸭 三个角度
vector dir = set(1,0,0);
matrix mat = ident();
rotate(mat, a, set(0,1,0));
dir *= mat;
vector newpos = @P + dir * f@len;
int newpt = addpoint(0, newpos);
int line = addprim(0, 'polyline', @ptnum, newpt);
//设置属性以便访问
setpointgroup(0, 'end', newpt, 1);
setpointattrib(0, 'len', newpt, f@len * 0.5); //长度每次变短
setpointattrib(0, 'ang', newpt, a);
}
setpointgroup(0, 'end', @ptnum, 0);6、3D L-系统树与递归
大概是使用下面这种方法实现的,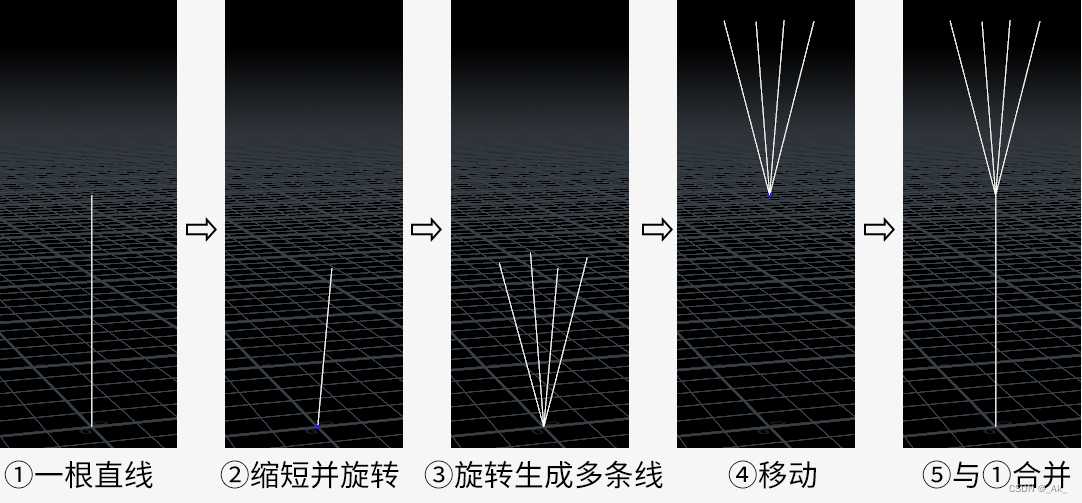
eg.①先上结果:(加各种随机参数、角度等等) ,
②节点连接及设置为,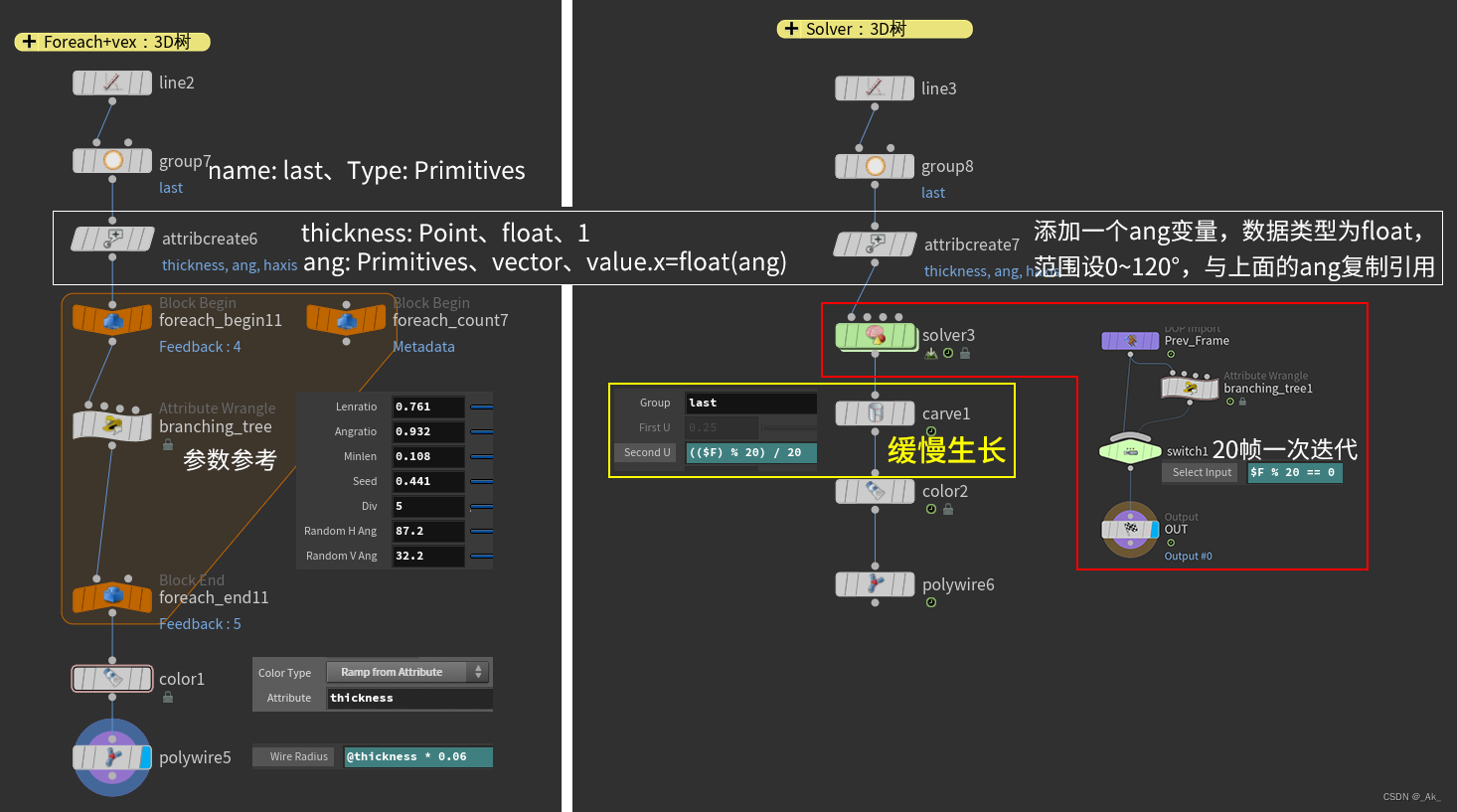
③ 类型为Primitives的branching_tree节点Group设为:last,完整代码为,(上面两个代码一样),
float branchang = radians(f@ang); // 分叉角度
float lenratio = chf('lenratio'); // 长度比例
float angratio = chf('angratio'); // 角度比例
float minlen = chf('minlen'); // 最小长度
int div = chi('div');
float seed = chf('seed');
int pts[] = primpoints(0, @primnum);
int pt1 = pts[0];
int pt2 = pts[1];
vector pos1 = point(0, 'P', pt1);
vector pos2 = point(0, 'P', pt2);
vector vaxis = normalize(pos2 - pos1); //水平轴
vector haxis = v@haxis; //垂直轴
float len = distance(pos1, pos2);
float thickness = point(0, 'thickness', pt2);
if(len < minlen){
return;
}
float range = radians(chf('random_h_ang'));
float randang = rand(seed * @primnum + 33.5);
randang = fit01(randang, -range, range);
matrix mat = ident();
rotate(mat, branchang + randang, haxis);
vector npos = pos2;
npos -= pos1;
npos *= mat;
npos *= lenratio;
for(int i=0; i<div; i++){
vector npos2 = npos;
float vang = $PI * 2.0 / div * i;
float range2 = radians(chf('random_v_ang'));
float randang2 = rand(seed * @primnum + 45.5 + i * 50.83);
randang2 = fit01(randang2, -range2, range2);
matrix mat2 = ident();
rotate(mat2, vang + randang2, vaxis);
npos2 *= mat2;
npos2 += pos2;
vector newhaxis = haxis;
newhaxis *= mat2;
int newpt = addpoint(0, npos2);
setpointattrib(0, 'thickness', newpt, thickness * lenratio);
int newline = addprim(0, 'polyline', pt2, newpt);
setprimgroup(0, 'last', newline, 1);
setprimattrib(0, 'haxis', newline, haxis);
setprimattrib(0, 'ang', newline, degrees(branchang * angratio));
}
setprimgroup(0, 'last', @primnum, 0);7、矩形细分与递归
摆烂,但还是记录下,毕竟最后一个了。
本次实现下面这种细分,
eg.①最终结果,
②节点连接及设置,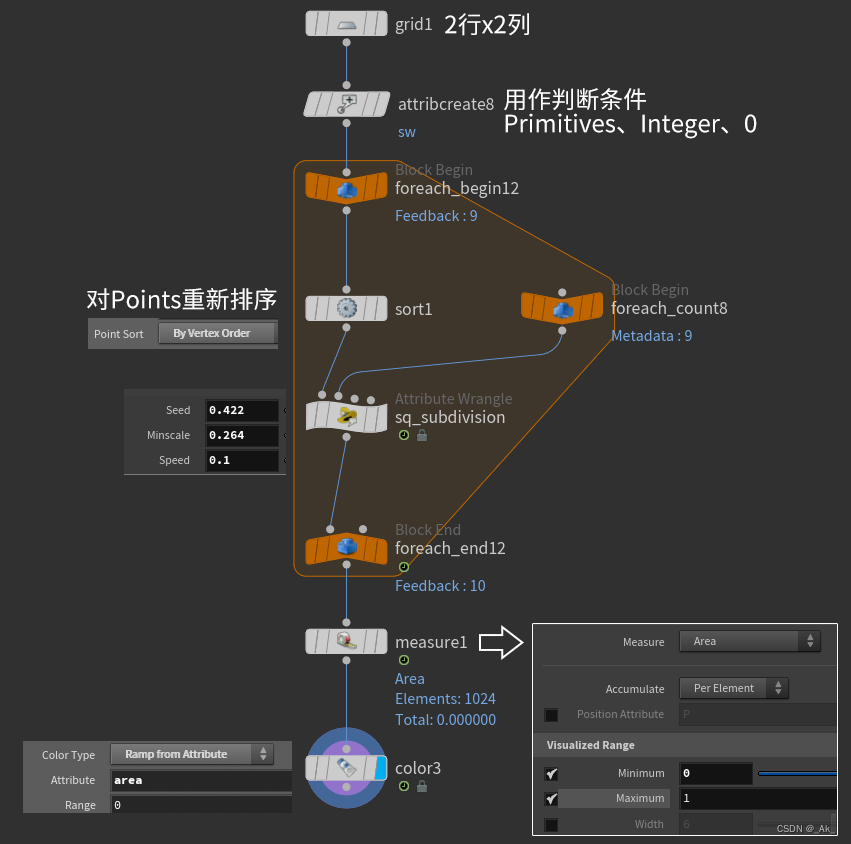
③ 类型为Primitives的sq_subdivision节点代码为,
int ite = detail(1, 'iteration');
int pts[] = primpoints(0, @primnum);
int sw = 1 - i@sw; // switch
float seed = chf('seed') + ite * 43.2 +@primnum * 4.6;
float randval = rand(seed);
float minscale = chf('minscale');
randval = fit01(randval, minscale, 1.0 - minscale);
randval += fit01(noise(seed + @Frame* chf('speed')), -minscale, minscale);
for(int i=0; i<2; i++){
int newprim = addprim(0, 'poly');
setprimattrib(0, 'sw', newprim, sw);
for(int n=0; n<len(pts); n++){
int pt = pts[n];
vector pos = point(0, 'P', pt);
vector opos = point(0, 'P', pts[0]); //第一个点
vector mpos = point(0, 'P', pts[2]); //第二个点,对角线的点
vector odir = pos - opos;
vector mdir = pos - mpos;
vector dir = set(0,0,0);
vector cpos = set(0,0,0);
if(sw == 0){
if(i == 0){
odir.x = odir.x * randval;
dir = odir;
cpos = opos;
}else{
mdir.x = mdir.x * (1.0 - randval);
dir = mdir;
cpos = mpos;
}
}else{
if(i == 1){
odir.z = odir.z * randval;
dir = odir;
cpos = opos;
}else{
mdir.z = mdir.z * (1.0 - randval);
dir = mdir;
cpos = mpos;
}
}
vector newpos = cpos + dir;
int newpt = addpoint(0, newpos);
addvertex(0, newprim, newpt);
}
}
removeprim(0, @primnum, 1);![HTML总结2 [转]](https://img-blog.csdnimg.cn/3d8a28eb78b04b62bbddd62cc1b8b2ed.png)