自定义绘制之图片

canvar.drawBitmap() ,BitMapFactory

  private fun getBitmap(width: Int): Bitmap? {
        val option = BitmapFactory.Options()
        option.inJustDecodeBounds = true
        BitmapFactory.decodeResource(resources, R.mipmap.android111,option)
        option.inJustDecodeBounds = false
        option.inDensity = option.outWidth
        option.inTargetDensity  = width
        return BitmapFactory.decodeResource(resources,R.mipmap.android111,option)
    }

加载本地图片优化版

inJustDecodeBounds  读取上下左右以及大小 等 信息

drawBitmap(bitmap,left,top,paint)

drawOval(left,top,right,bottom) 画椭圆

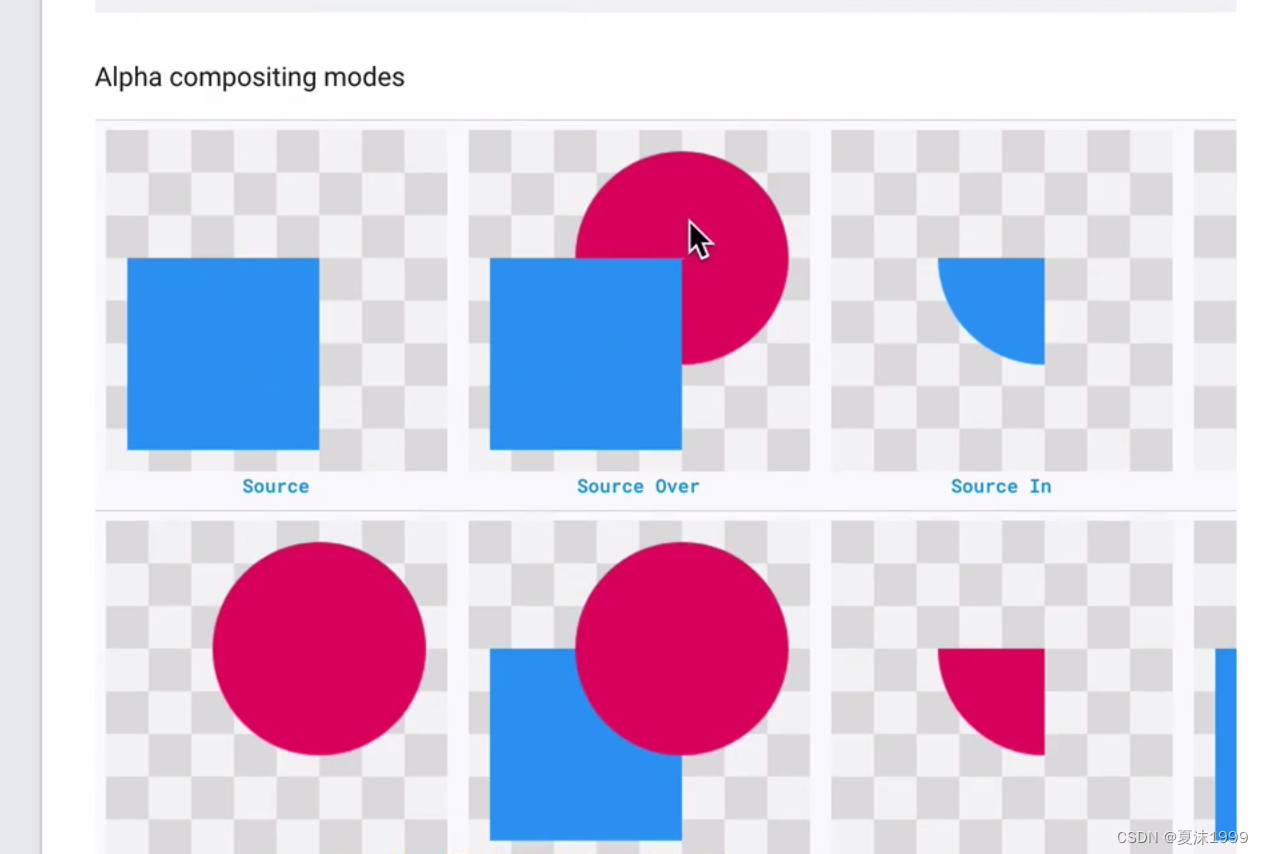
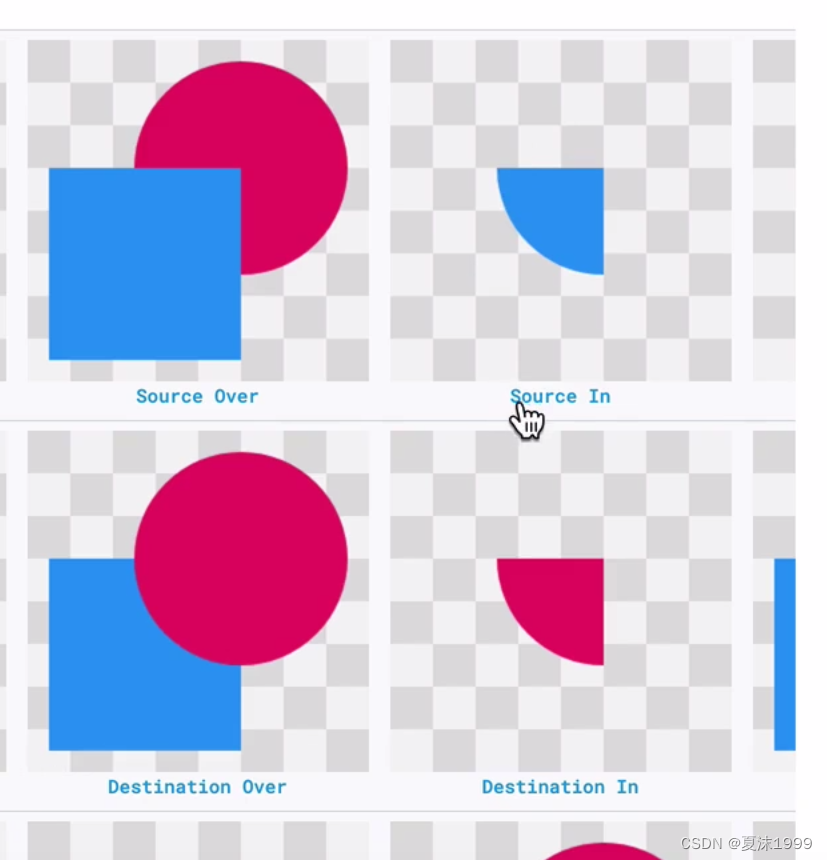
paint.setXfremode() // 现在只剩一种 PorterDuffXfermode

val count = canvar.saveLayer(bounds,paint) 挖空的区域 返回ocunt

bounds = RectF() 

cavar.restoreToCouint 还原位置 

tips:使用完成后 最好恢复一下

paint.xfermode = null
canvas.restoreToCount(count)

 

 

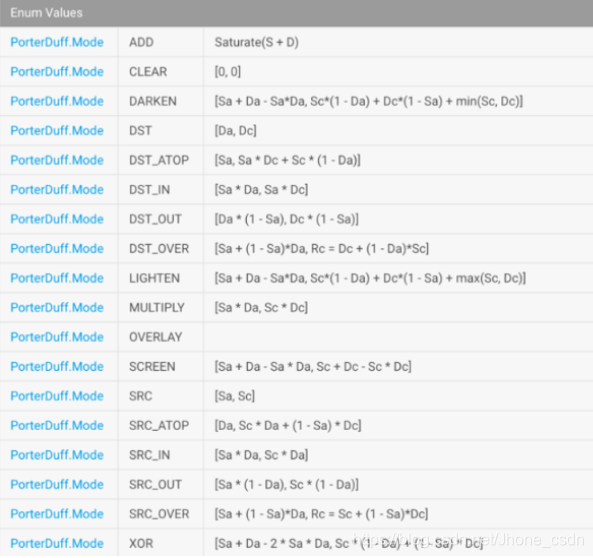
算法

 

 

canvar.drawOval(left,top,right,bottom,paint) 绘制圆形 椭圆

canvar.drawRect(left,top,right,bottom,paint) 绘制方形

Mode: SRC_IN,SRC,SRC_OVAL等,绘制时会根据范围进行判断进行绘制,可能出现与Mode方式不同的结果,透明区域也要计算