本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。
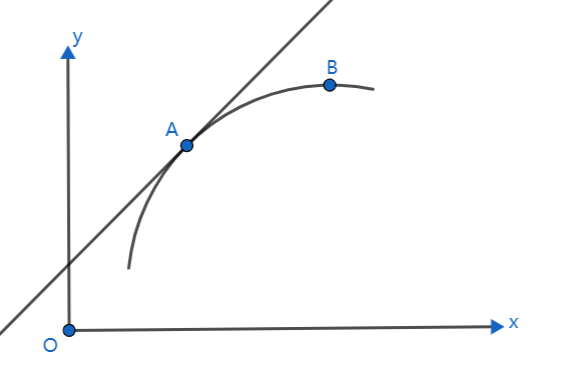
如上图所示。
设
y
=
f
(
x
)
,
x
=
φ
(
t
)
,
y
=
ψ
(
t
)
当
t
=
t
0
时,
x
=
x
0
,
y
=
y
0
,即点
A
坐标为
(
x
0
,
y
0
)
点
A
处的导数
f
′
(
x
0
)
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
t
→
0
ψ
(
t
0
+
Δ
t
)
−
ψ
(
t
0
)
φ
(
t
0
+
Δ
t
)
−
φ
(
t
0
)
=
lim
Δ
t
→
0
ψ
(
t
0
+
Δ
t
)
−
ψ
(
t
0
)
Δ
t
/
φ
(
t
0
+
Δ
t
)
−
φ
(
t
0
)
Δ
t
=
lim
Δ
t
→
0
ψ
(
t
0
+
Δ
t
)
−
ψ
(
t
0
)
Δ
t
/
lim
Δ
t
→
0
φ
(
t
0
+
Δ
t
)
−
φ
(
t
0
)
Δ
t
=
ψ
′
(
t
0
)
φ
′
(
t
0
)
因此点
A
处的切线向量可表示为
(
ψ
′
(
t
0
)
,
φ
′
(
t
0
)
)
而切线方程为
y
−
y
0
=
ψ
′
(
t
0
)
φ
′
(
t
0
)
(
x
−
x
0
)
,即
y
−
y
0
ψ
′
(
t
0
)
=
x
−
x
0
φ
′
(
t
0
)
同理可得空间直线的点向式方程为:
y
−
y
0
ψ
′
(
t
0
)
=
x
−
x
0
φ
′
(
t
0
)
=
z
−
z
0
ω
′
(
t
0
)
如上图所示。\\ 设y=f(x),x=\varphi(t),y=\psi(t) \\ 当t=t_0时,x=x_0,y=y_0,即点A坐标为(x_0,y_0) \\ 点A处的导数f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\varphi(t_0+\Delta t)-\varphi(t_0)} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\lim_{\Delta t \to 0}\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)} \\ \,\\ 因此点A处的切线向量可表示为(\psi^\prime(t_0),\varphi^\prime(t_0)) \\ 而切线方程为y-y_0=\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)}(x-x_0),即\frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)} \\ \,\\ 同理可得空间直线的点向式方程为:\\ \frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)}=\frac{z-z_0}{\omega^\prime(t_0)}
如上图所示。设y=f(x),x=φ(t),y=ψ(t)当t=t0时,x=x0,y=y0,即点A坐标为(x0,y0)点A处的导数f′(x0)=Δx→0limΔxΔy=Δt→0limφ(t0+Δt)−φ(t0)ψ(t0+Δt)−ψ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δtφ(t0+Δt)−φ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δt→0limΔtφ(t0+Δt)−φ(t0)=φ′(t0)ψ′(t0)因此点A处的切线向量可表示为(ψ′(t0),φ′(t0))而切线方程为y−y0=φ′(t0)ψ′(t0)(x−x0),即ψ′(t0)y−y0=φ′(t0)x−x0同理可得空间直线的点向式方程为:ψ′(t0)y−y0=φ′(t0)x−x0=ω′(t0)z−z0
专题:平面、空间直线参数方程下的切线斜率问题
news2026/3/5 8:56:41
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/934822.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
拼多多开放平台的API接口可以获取拼多多电商数据。以下是API接口流程
使用拼多多开放平台的API接口可以获取拼多多电商数据。以下是一般的API接口流程:
1. 注册开发者账号:首先,您需要在拼多多开放平台注册一个开发者账号。通过开发者账号,您可以获得API密钥和其他必要的信息。
2. 鉴权与认证&…
最详细的Django安装与启动
Django安装与配置
Python支持版本:
Django 3.2支持的Python版本为3.6、3.7、3.8和3.9,而Django 4.1只支持Python 3.8、3.9和3.10。
因为考虑到新的python版本更新和新的mysql数据库版本,由此使用 python3.8和Django 4.1和MYSQL8.0
Django…
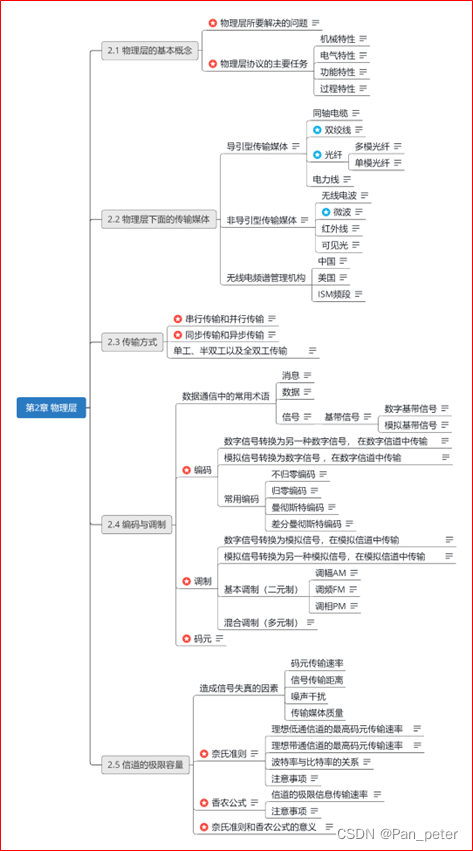
计算机网络-笔记-第二章-物理层
目录
二、第二章——物理层
1、物理层的基本概念
2、物理层下面的传输媒体
(1)光纤、同轴电缆、双绞线、电力线【导引型】
(2)无线电波、微波、红外线、可见光【非导引型】
(3)无线电【频谱的使用】 …
统计学补充概念-17-线性决策边界
概念
线性决策边界是一个用于分类问题的线性超平面,可以将不同类别的样本分开。在二维空间中,线性决策边界是一条直线,将两个不同类别的样本分隔开来。对于更高维的数据,决策边界可能是一个超平面。 线性决策边界的一般形式可以表…
如何查看友商的Camera配流情况
有时候,我们想看下竞品友商机器上,使用到camera的app 申请的分辨率情况。
如果只是抓logcat日志,我们可能没法从中获取到有效信息,毕竟一般出货的机器版本,基本已经把大部分相关日志都给关闭了。
那有没其它方式&…
画出你的数据故事:Python中Matplotlib使用从基础到高级
摘要: Matplotlib是Python中广泛使用的数据可视化库,它提供了丰富的绘图功能,用于创建各种类型的图表和图形。本文将从入门到精通,详细介绍Matplotlib的使用方法,通过代码示例和中文注释,帮助您掌握如何在不…
java练习8.100m小球落地
题目: 如一个小球从100米高度自由落下,每次落地后就反跳回原高度的一半。
那么求它在第10次落地时,共经过多少米?第10次反弹多高? public static void main(String[] args) {/*假如一个小球从100米高度自由落下,每次落…
五种重要的 AI 编程语言
推荐:使用 NSDT场景编辑器 助你快速搭建3D应用场景 简而言之:决定从哪种语言开始可能会令人生畏。
不用担心!本文将解释 AI 中使用的最流行编程语言背后的基础知识,并帮助您决定首先学习哪种语言。对于每种语言,我们将…
如何通过开源项目学习编程?
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…
[LitCTF 2023]Flag点击就送!
进入环境后是一个输入框,可以提交名字 然后就可以点击获取flag,结果回显提示,需要获取管理员 可以尝试将名字改为admin 触发报错,说明可能存在其他的验证是否为管理员的方式 通过抓包后,在cookie字段发现了 特殊的东西…
服务器安全-修改默认ssh端口
防火墙先打开指定端口,要不修改后连不上(端口需要在65535之内)
firewall-cmd --list-ports
firewall-cmd --add-port54111/tcp --permanent
firewall-cmd --reload--------------------
先让两个端口同时存在,等配置成功后关闭22端口
vim /etc/ssh/sshd_config重启sshd
service…
2023年最新版Windows环境下|Java8(jdk1.8)安装教程
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【JavaSE_primary】 jdk1.8的下载和使用总共分为3个步骤: jdk1.8的下载、jdk1.8的安装、配置环境变量。 目录 一、jdk1.8下载…
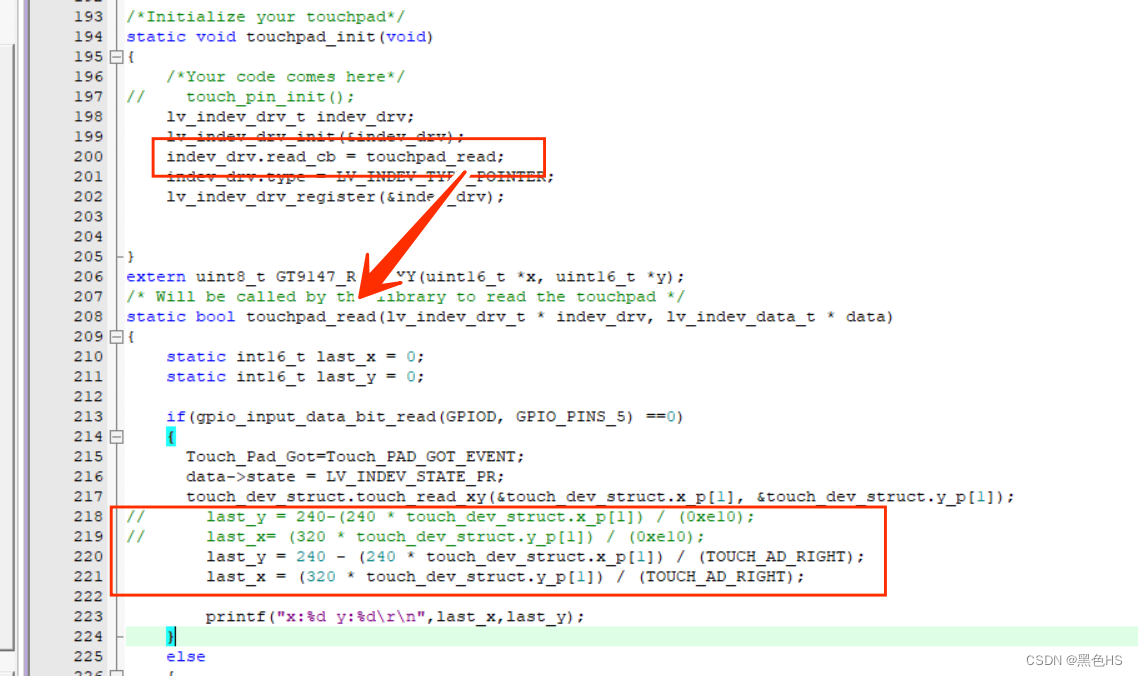
GUI GUIDER生成的GUI移植到雅特力MCU平台过程详解(ST/GD/国民/极海通用)
好记性不如烂笔头,既然不够聪明,就乖乖的做笔记,温故而知新。 本文档用于本人对知识点的梳理和记录 一、前言
上一篇我们有介绍NXP GUI Guider工具如何制作和调试GUI,GUI神器 NXP GUI GUIDER开发工具入门教程https://blog.csdn.n…
寄存柜让物品存储变得更简单
寄存柜是一种提供临时性物品寄存服务的设备,通常用于超市、商场、机场、火车站、学校、影院、体育馆等公共场所为用户提供便捷的寄存服务。 寄存柜的种类: 1.行李寄存柜:专门用于旅行者寄存行李和物品的柜子,通常位于机场、火车站…
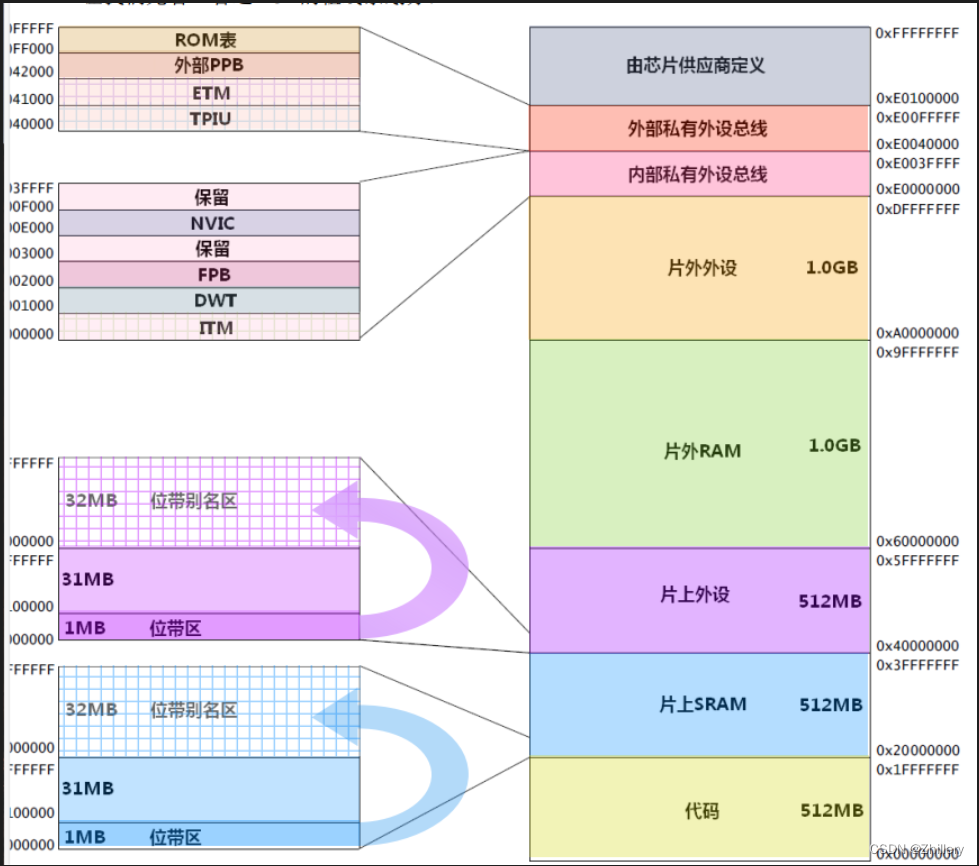
【Cortex-M3权威指南】学习笔记3 - 存储系统
目录 存储系统存储器映射存储器各种访问属性存储器的缺省访问许可位带操作非对齐数据传输互斥访问端模式 存储系统 存储器映射
CM3 预定义存储器映射简图(CM3 的地址空间是 4GB ) 片上 SRAM:大小 512MB,拥有 1MB 位带区ÿ…
SAP MTS案例教程STO公司间采购前台操作
目录 本章介绍 2 STO主数据操作 3 新增公司间物料(部件公司) 3 新增公司间供应商(整机公司) 9 新增公司间客户(部件公司) 13 STO 计划MRP相关操作 17 新增STO公司间采购订单(整机公司) 17 部件公司计划…
uvm_sequence_library 中添加sequence类型的两种方式
uvm_sequence_library是从uvm_sequence扩展而来的,它是一个容纳了一系列其它sequences类型的容器,在启动时,它会根据模式从这系列sequences中选择并执行它们。如果处于UVM_SEQ_LIB_RAND模式,它的select_rand属性将会随机并作为选择…
集合框架-(Collection/Map)
1.单列集合
1.1基础概要
集合中存储的是对象的地址信息,想要输出对象的信息,需要在具体的类中重写toString()方法 Collection代表单列集合,每个元素数据只包含一个值 List集合:添加的元素可以是有序、可…
时序预测 | MATLAB实现DBN-SVM深度置信网络结合支持向量机时间序列预测(多指标评价)
时序预测 | MATLAB实现DBN-SVM深度置信网络结合支持向量机时间序列预测(多指标评价) 目录 时序预测 | MATLAB实现DBN-SVM深度置信网络结合支持向量机时间序列预测(多指标评价)效果一览基本描述程序设计参考资料 效果一览 基本描述 MATLAB实现DBN-SVM深度置信网络结合支持向量机…






![[LitCTF 2023]Flag点击就送!](https://img-blog.csdnimg.cn/229f00f8cc464f40a38838a3aa128f78.png)