树型结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合
- 树是递归定义的。
- 树形结构中,子树之间不能有交集,否则就不是树形结构
树与非树

概念(重要)



树的表示形式
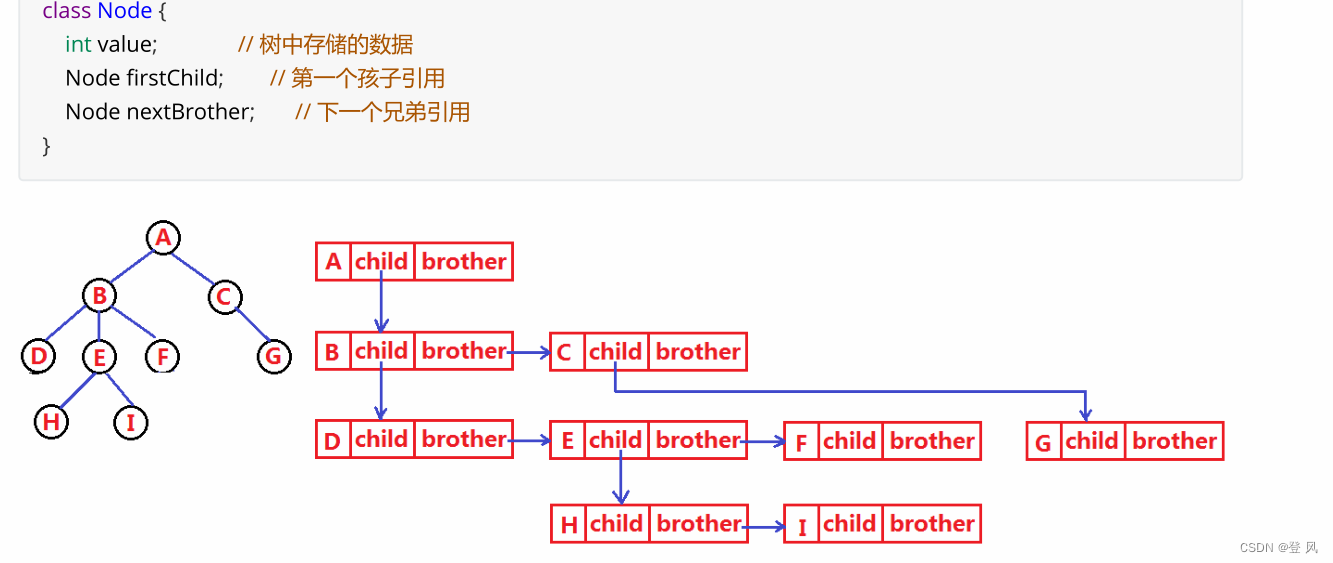
最常用的孩子兄弟表示法
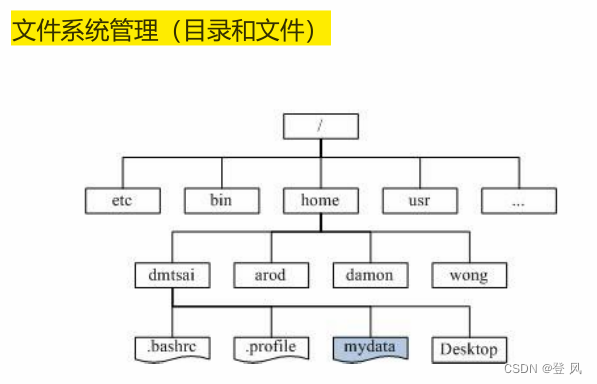
树的应用
二叉树
概念
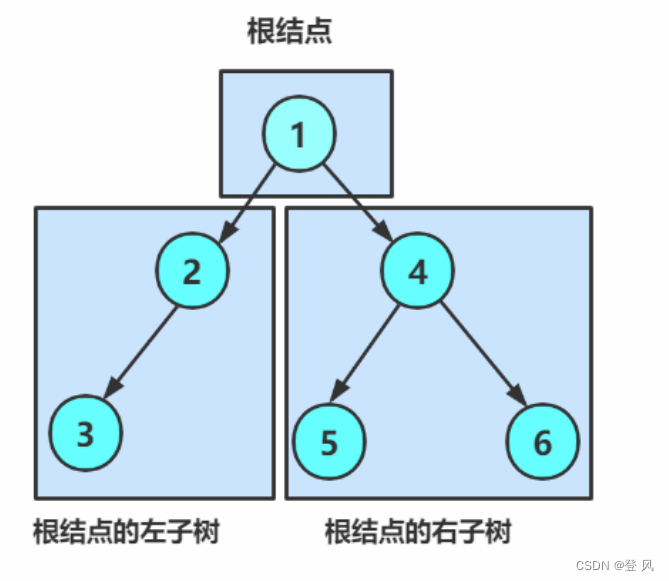
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
 1. 二叉树不存在度大于2的结点
1. 二叉树不存在度大于2的结点
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
两种特殊的二叉树
满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。
如果一棵二叉树的层数为K,且结点总数是(2^k)-1 ,则它就是满二叉树。
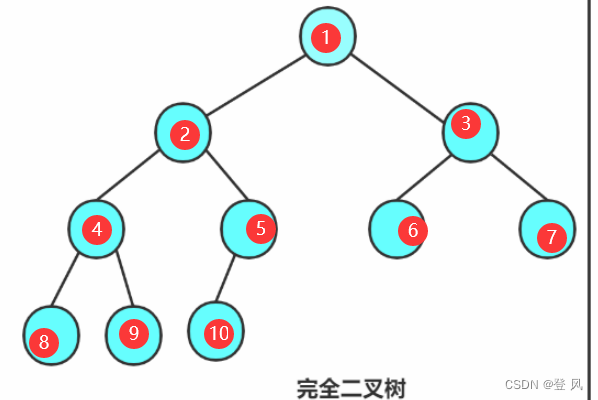
完全二叉树: 对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。如下

二叉树的性质










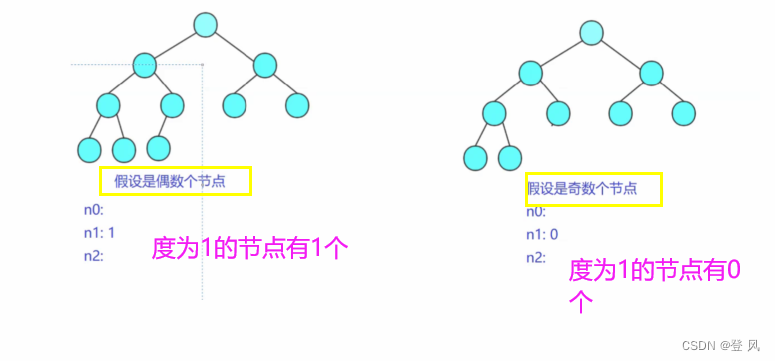



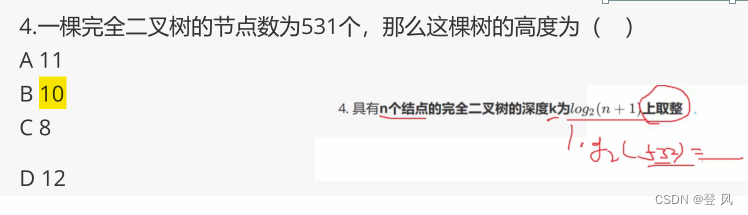
二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式

这里我们使用孩子表示法
二叉树的基本操作
简单的创建一棵树
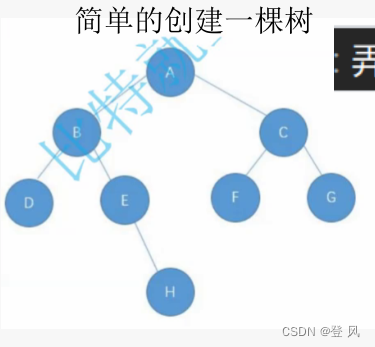
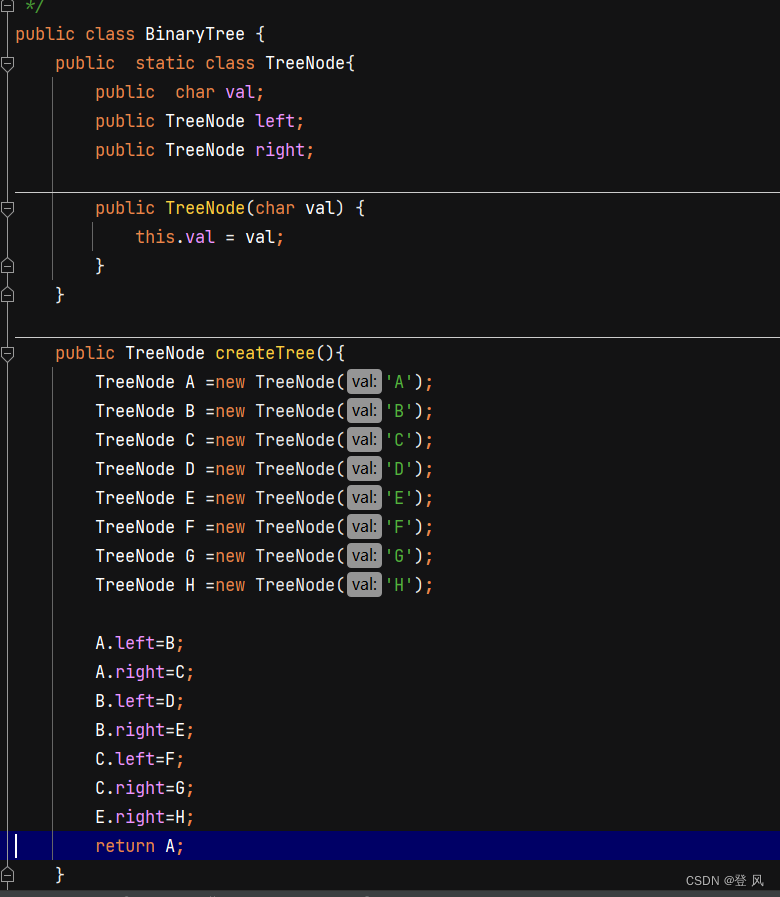
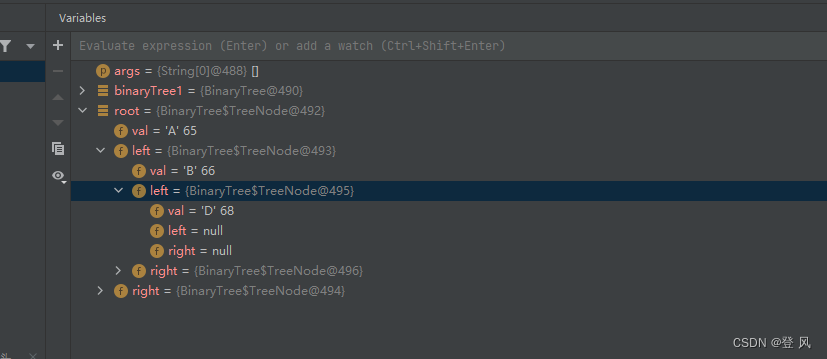
二叉树的遍历
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点。

遇到左子树和右子树都不打印,遇到根时才打印
前序遍历
根,左子树,右子树
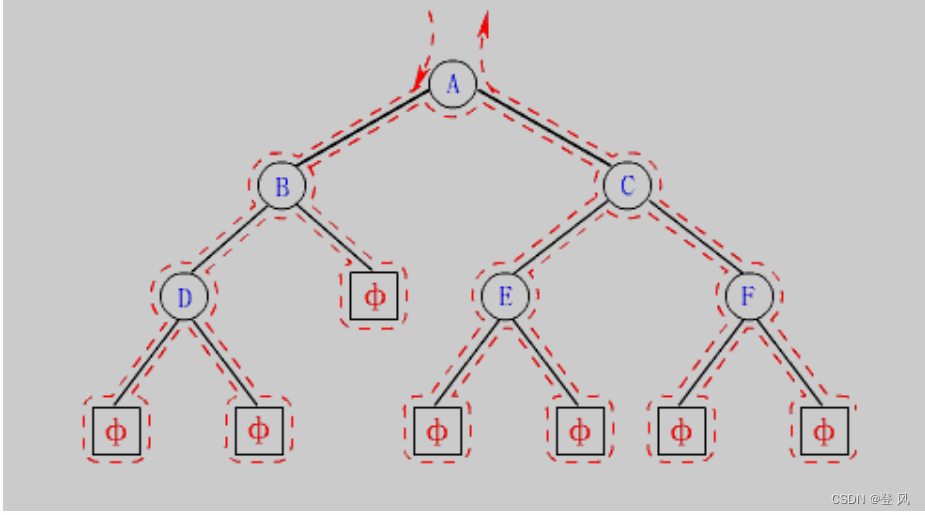
首先进入的是根,则打印根A;然后走左子树,左子树的第一个节点B又可以看作是根,打印根B;之后再走左子树,左子树的第一个节点是D,D又可以看作是根,打印D;走左子树,左子树为null,走右子树,右子树为null;则以D为根的这棵树结束。返回到D。D作为上一次的左子树,走右子树,右子树为null;则以B为根的这棵树结束,返回到B。B作为上上一次的左子树,走右子树C,C又可以看作是根,则打印C;之后走左子树…依次如此。
上述前序遍历的结果是A,B,D,C,E,F
中序遍历
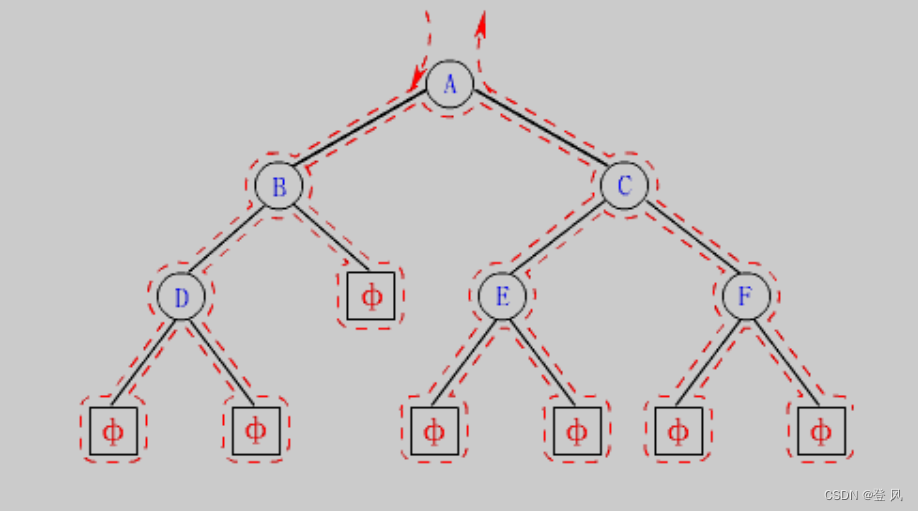
左子树,根,右子树
中序遍历的结果是:D,B,A,E,C,F
后序遍历
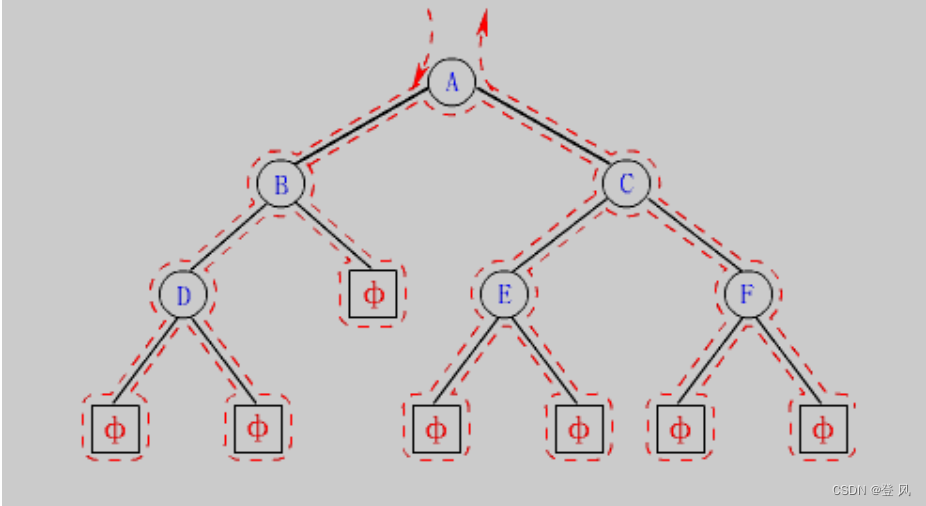
左子树,右子树,根
上述后序遍历的结果是:D,B,E,F,C,A

层序遍历
层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层
上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

上述层序遍历的结果为:A,B,C,D,E,F

完全二叉树可以保证前k-1层为全满状态
于是
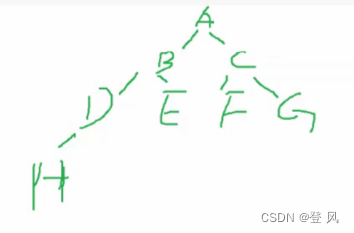
前序遍历为:A,B,D,H,E,C,F,G

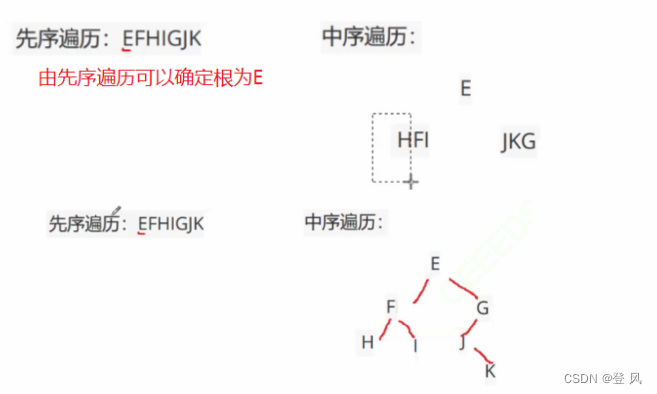

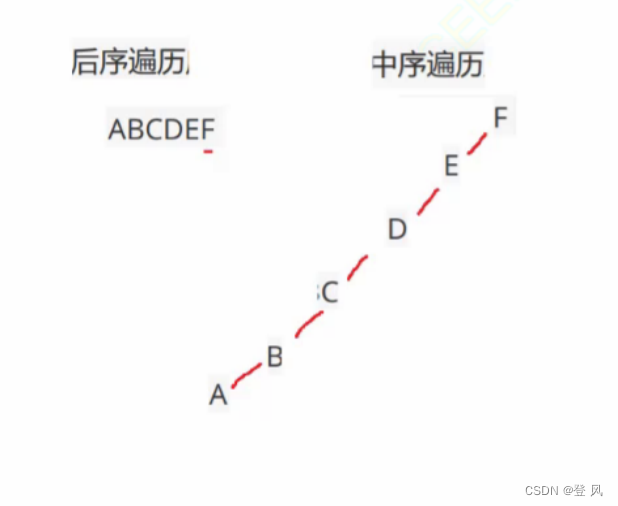
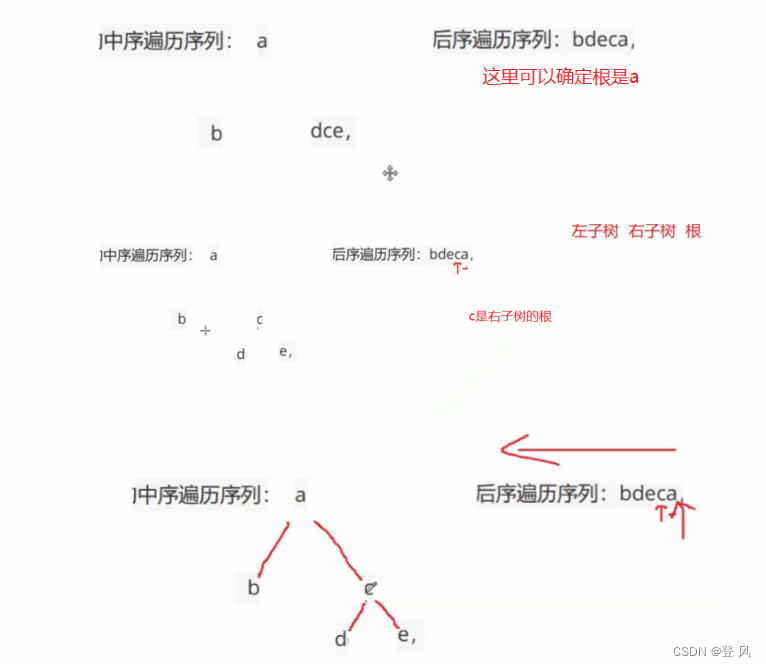 选D
选D

二叉树的基本操作
前序遍历
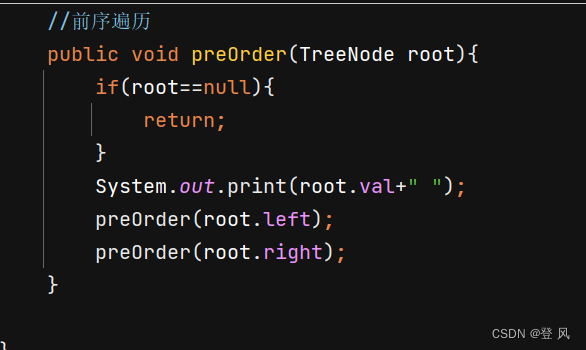
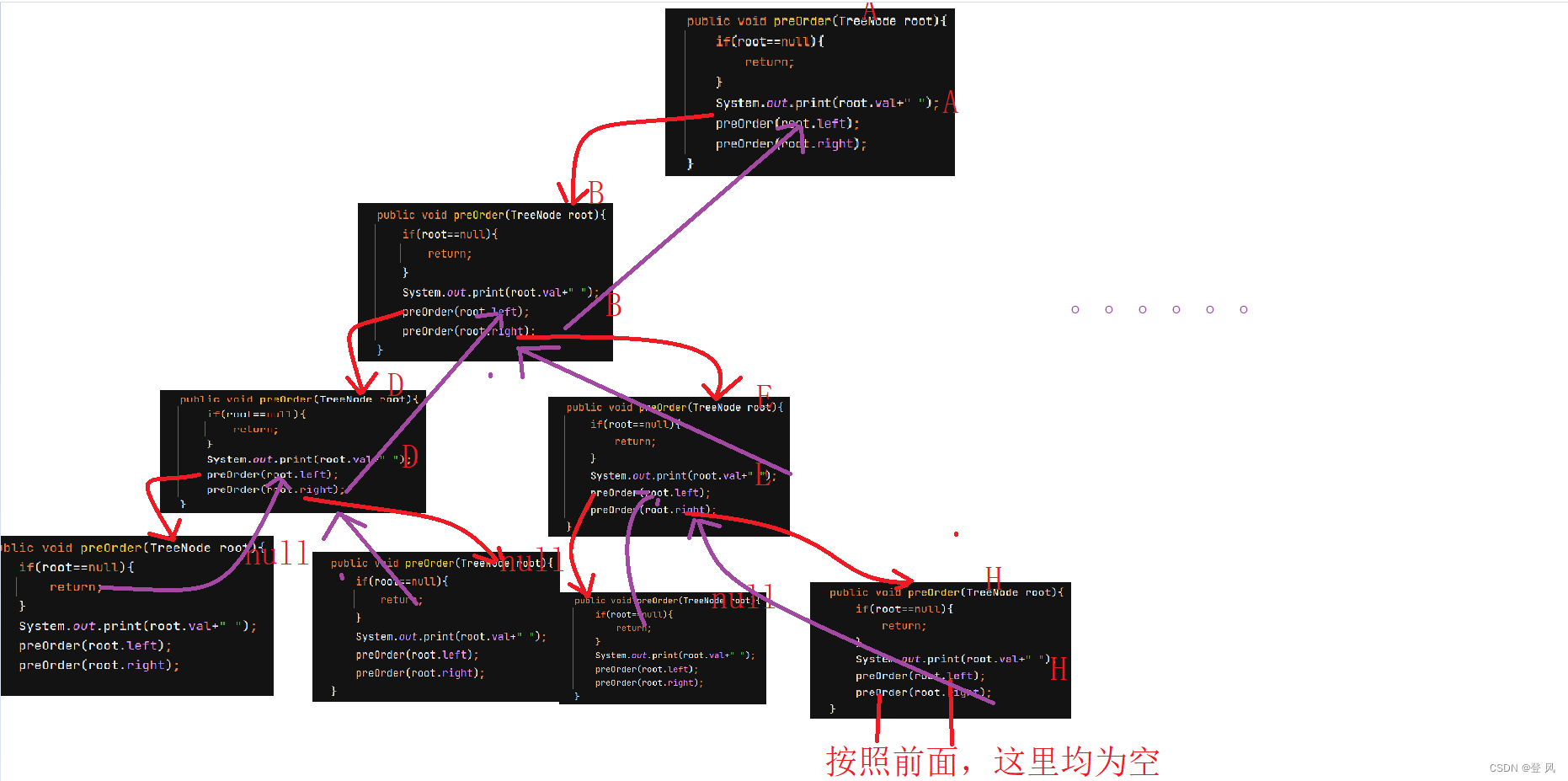
带有返回值的前序遍历


结果如下:
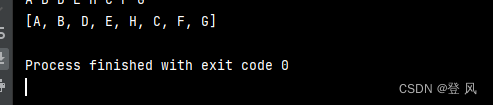
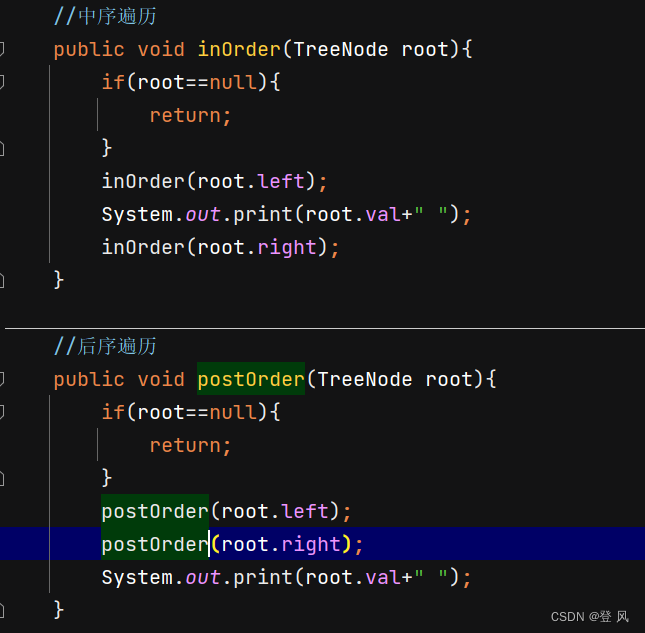
三种遍历的区别在于具体在什么时机去打印元素
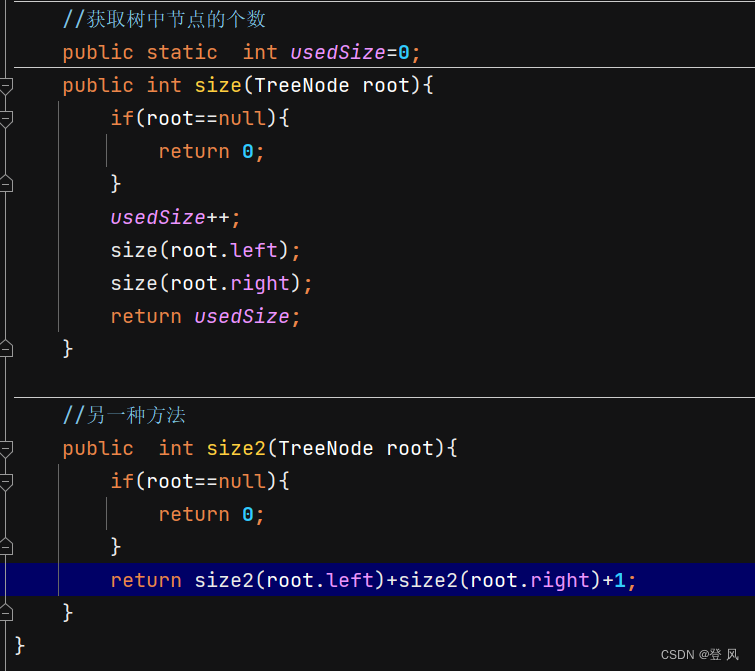
获取树中节点的个数

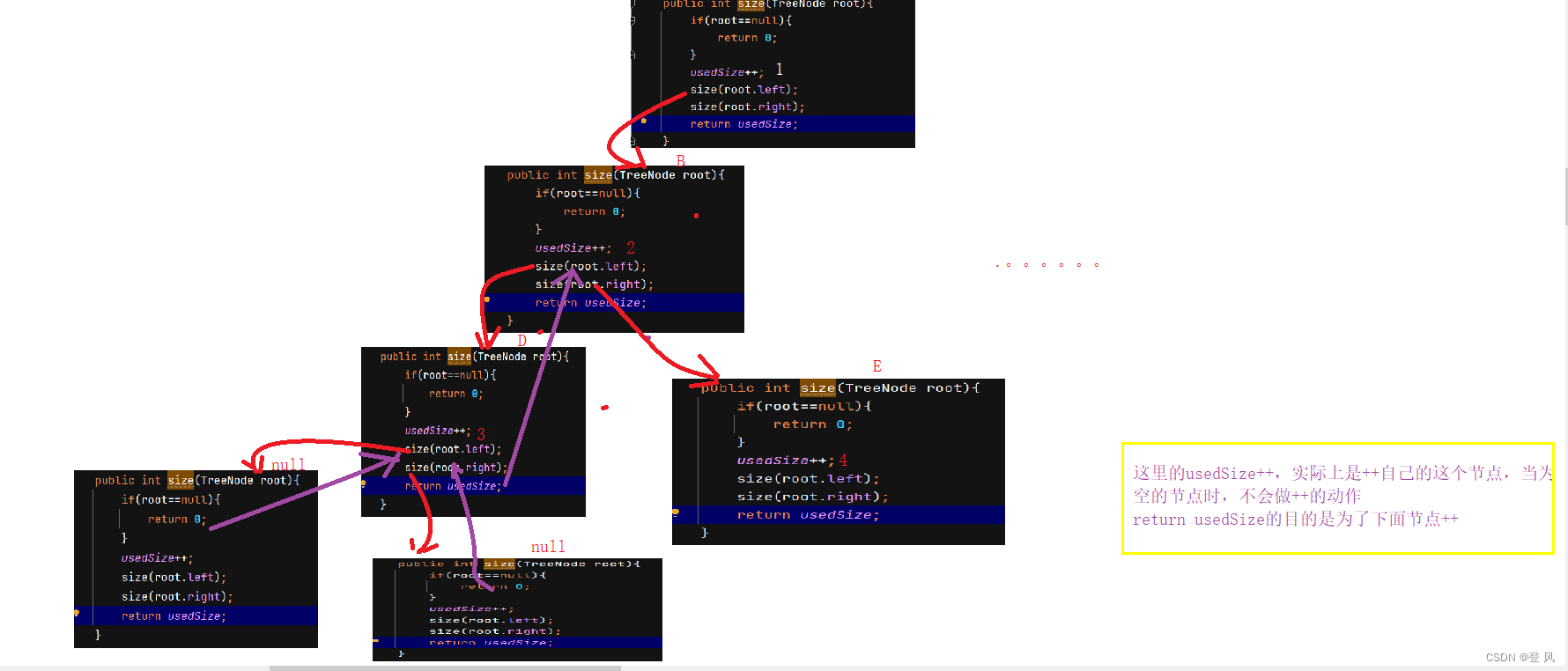
结果如下

获取叶子节点的个数

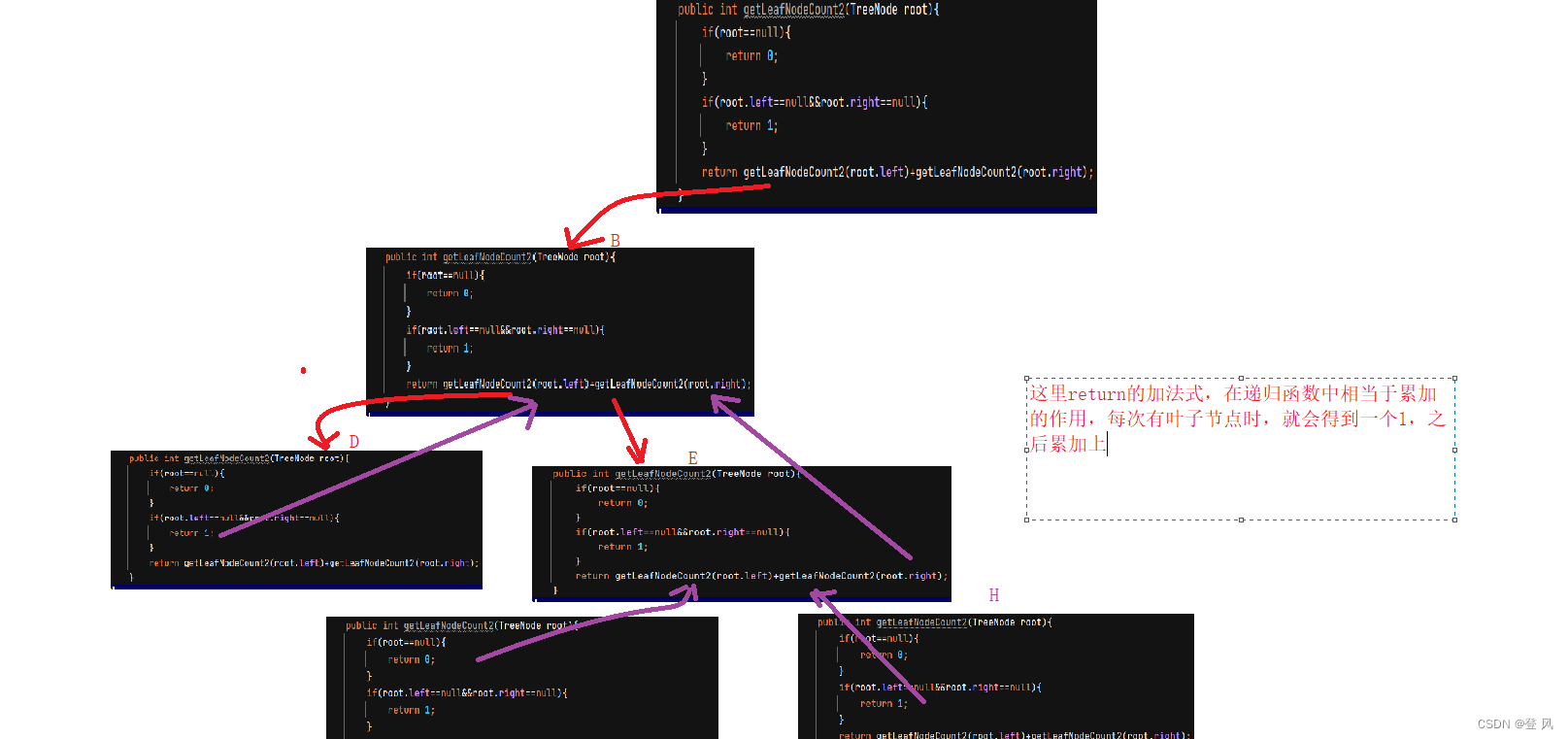

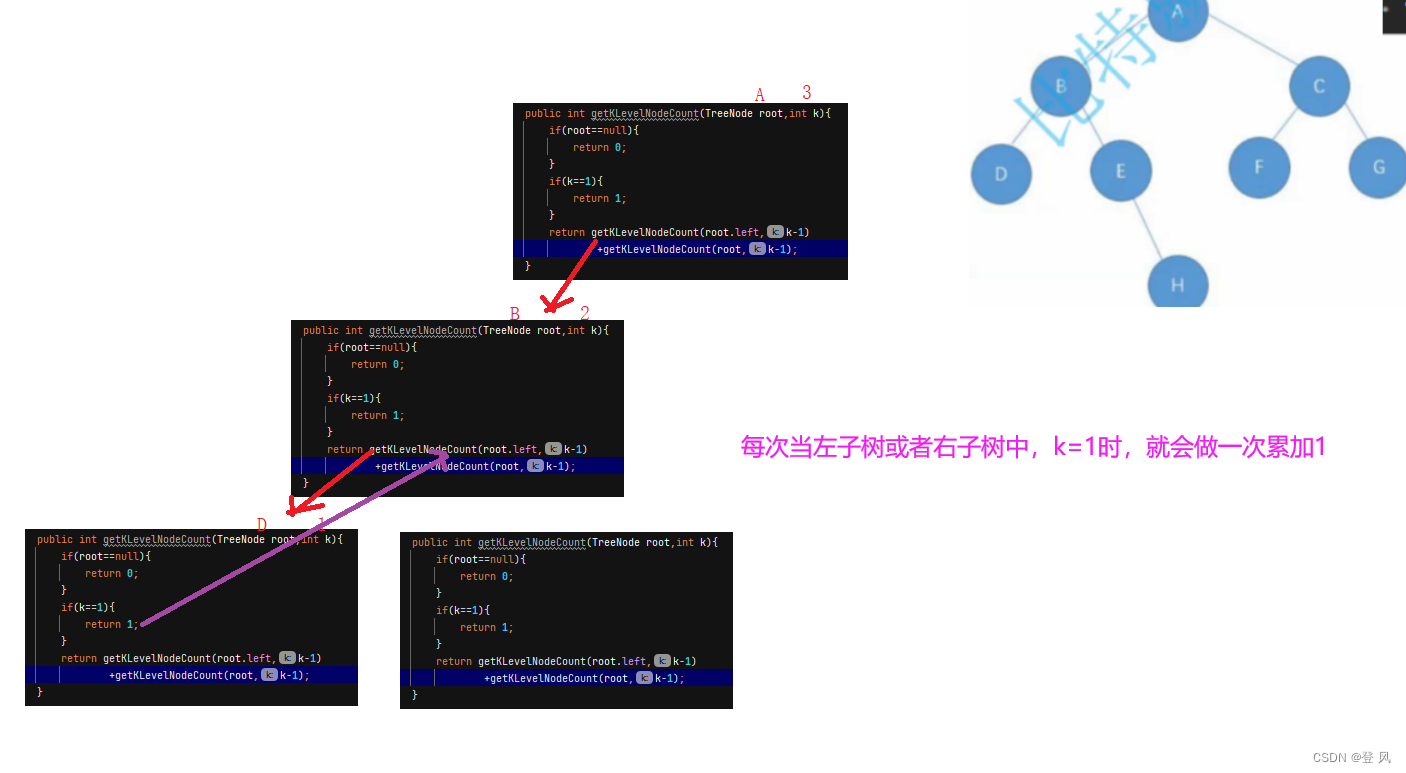
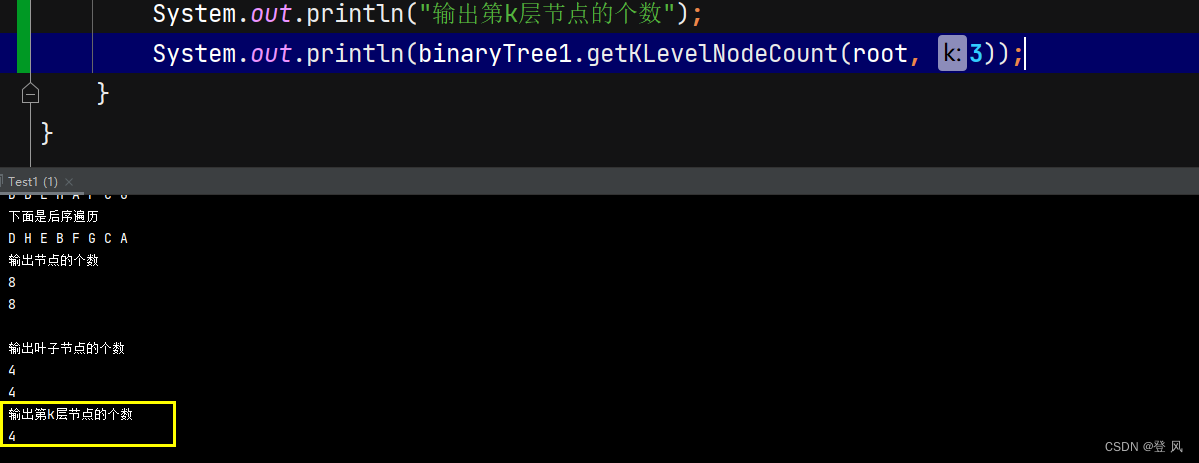
获取第K层节点的个数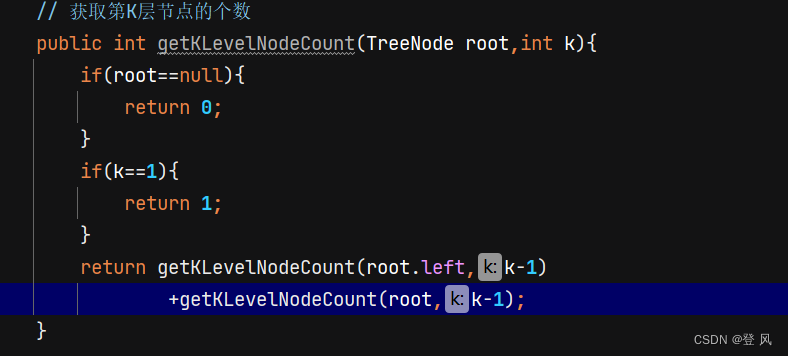






![Vue3 [Day11]](https://img-blog.csdnimg.cn/454dfbf535164b378fb15c4f22c78773.png)