有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

提示:

• 1 <= points.length <= 105
• points[i].length == 2
• ≤xstart ≤ x ≤ xend≤

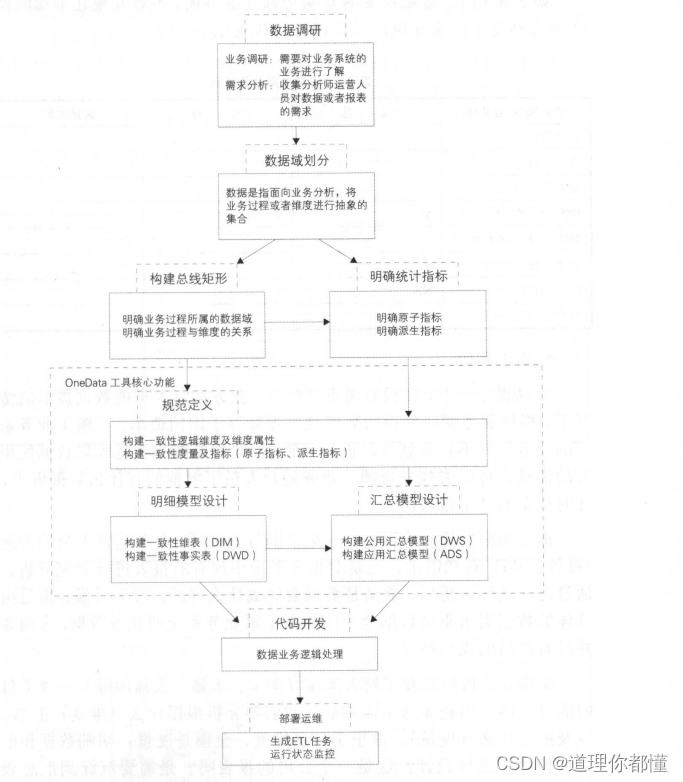
解法（贪心算法 -- 难度[高]）：

class Solution {

    public int findMinArrowShots(int[][] points) {

        if(points.length == 0) return 0;

        // 从第1个气球开始，第0个气球本身就需要一只箭
        int res = 1;

        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if(o1[0] < o2[0]){
                    return -1;
                }
                return 1;
            }
        });

        for (int i = 1; i < points.length; i++) {
            // 前后不相交
            if(points[i-1][1] < points[i][0]){
                res++;
            }else{
                // 相交，移动区间(让一只箭射穿最多个气球)
                points[i][1] = Math.min(points[i-1][1], points[i][1]);
            }
        }

        return res;
    }
}

细节：

对比函数越界，注意区间

 ≤xstart ≤ x ≤ xend≤

是 int 的边界，如果使用传统的o1[0] - o2[0]，当两个都是负结尾或者正结尾，会发生溢出，因此使用大于小于判断。

Arrays.sort(points, new Comparator<int[]>() {
    @Override
    public int compare(int[] o1, int[] o2) {
        if(o1[0] < o2[0]){
            return -1;
        }
        return 1;
    }
});