codeforce 894

news2024/11/15 10:51:41

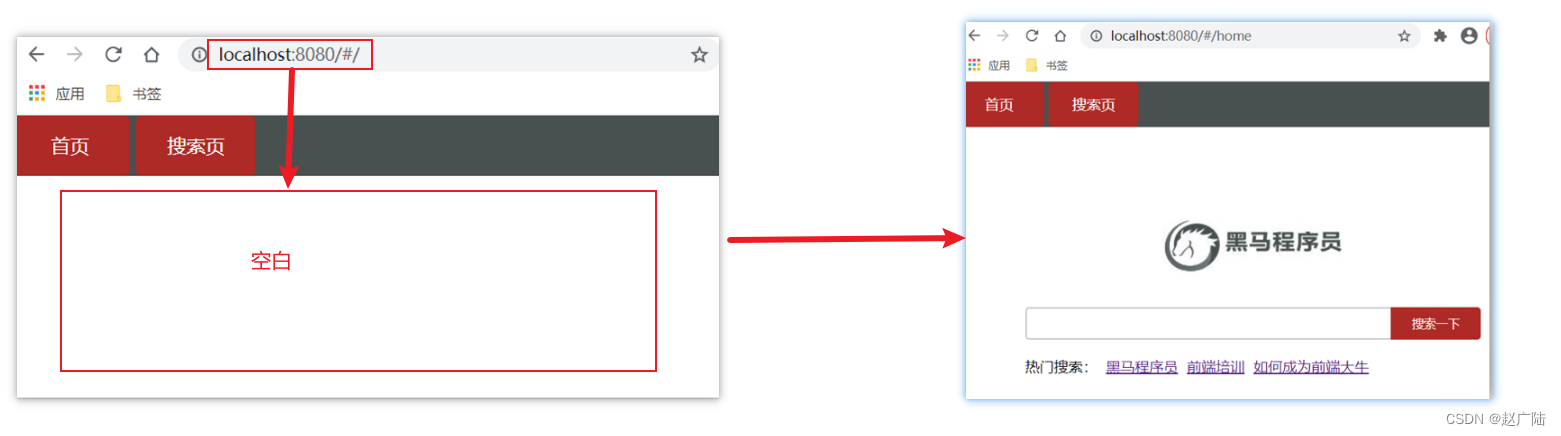
A. Gift Carpet （模拟）

题意：
给出n*m的矩阵，从左到右每列最多取一个字母，问能否取出"vika"
思路：
直接模拟。

const int N=1e6+10;
char g[25][25];
void solve(){
    int n,m; cin>>n>>m;
    string s="vika";
    for(int i=0;i<n;i++){
        getchar();
        for(int j=0;j<m;j++){
            g[i][j]=getchar();
        }
    }
    int j=0;
    bool flag=true;
    for(char c:s){
        bool ok=false;
        for(;j<m;j++){
            for(int i=0;i<n;i++){
                if(g[i][j]==c){
                    ok=true;
                    break;
                }
            }
            if(ok) {
                j++;
                break;
            }
        }
        if(!ok) {
            flag=false;
            break;
        }
    }
    if(flag) printf("YES\n");
    else printf("NO\n");
}
int main(){
    int t; cin>>t;
    while(t--){
        solve();
    }
}

B. Sequence Game （构造）

题意：
假设有一个序列a1…an, 我们要根据题目给出的序列b1…bm猜出序列a1…an。b1…bm是这样来的：

b1 == a1
遍历a2…an，如果发现 ${a_{i-1}<=a_{i}}$ ，则将 ${a_i}$ 加入b序列。

比如a序列是 $4, 3, 2, 6, 3, 3$ ，那么对应的b序列是 $4, 6, 3$ 。现在给出b序列，要求输出a序列。

思路：
构造出一个符合条件的序列即可。a序列如果是 $4, 6, 6, 3$ ，那么就能得到 $4, 6, 3$ 这样的b序列。

const int N=2e5+10;
int a[N];
void solve(){
    int n; cin>>n;
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    vector<int> res;
    res.push_back(a[0]);
    for(int i=1;i<n;i++){
        if(a[i-1]>a[i]) res.push_back(a[i]);
        res.push_back(a[i]);
    }
    printf("%d\n",res.size());
    for(int i=0;i<res.size();i++){
        if(i==0) printf("%d",res[i]);
        else printf(" %d",res[i]);
    }
    printf("\n");
}
int main(){
    int t; cin>>t;
    while(t--){
        solve();
    }
}

C. Flower City Fence （模拟）

题意
给出一个序列 $a 1.. an$ ，那么在xy坐标轴上面可以形成一个柱状图：
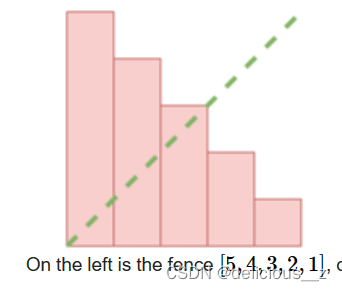
在这里插入图片描述
然后题目问你，如果把它转置之后（行转成列，列变成行）是否能得到一样的柱状图。

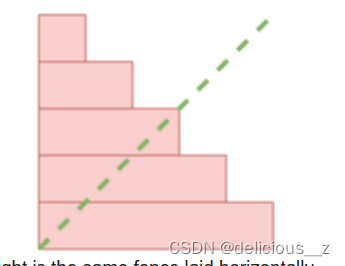
思路
令转置之前的高度序列为 $H_{1}, H_2 ... H_n$ ，
转置之后的高度序列为 $h_1,h2...h_m$
然后比较这两个序列是不是相同就可以了。

const int N=2e5+10;
int a[N];
void solve(){
    int n; cin>>n;
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    if(a[0]!=n){
        printf("NO\n");
        return;
    }
    vector<int> b(n);
    int p=n;
    for(int h=0;h<n;h++){
        for(;p>=0;){
            if(a[p-1]>h) break;
            else p--;
        }
        b[h]=p;
    }
    bool ok=true;
    for(int i=0;i<n;i++){
        if(a[i]!=b[i]){
            ok=false;
            break;
        }
    }
    if(ok) printf("YES\n");
    else printf("NO\n");
}
int main(){
    int t; cin>>t;
    while(t--){
        solve();
    }

D. Ice Cream Balls

题意
两个材料可以制作出一种冰淇淋。例如：
以 ${1,1,2}$ 为原材料，能制作出 ${1,1}$ 和 ${1,2}$ 两种不同类型的冰淇淋。
现在假设有x个材料，刚好能制作出n冰淇淋。题目给出n，求x。

思路
我们将n*(n-1)/2的序列打印出来看，能发现一些规律：

2*(2-1)/2=1
3*(3-1)/2=3
4*(4-1)/2=6
5*(5-1)/2=10
6*(6-1)/2=15
7*(7-1)/2=21
8*(8-1)/2=28
9*(9-1)/2=36
10*(10-1)/2=45
11*(11-1)/2=55

${1,2}$ 可以制作出1种；
${1,2,3}$ 可以制作出3种；
${1,2,3,4}$ 可以制作出6种。
但是题目给出的n有可能不是 $n * (n - 1) /2$ ，比如要制作5种，那么就得构造 $1, 2, 3, 2, 3$ ，那么n=5对应的x就是5。
也就是说n=5的时候，

我们先找到x=3，由于 $3 * (3 - 1) /2 = 3$ ，还差2种
那么x=3+2=5.

关于n=5的时候怎么找到x=3，我这里用了二分，但是看别人的题解好像不用二分直接从1开始暴力找也行。

void solve(){
    ll n; cin>>n;
    ll l=1,r=1e10;
    ll ans=0;
    while(l<=r){
        ll mid=(l+r)/2;
        if(mid*(mid-1)/2 <= n){
            ans=mid;
            l=mid+1;
        } else {
            r=mid-1;
        }
    }
    ans+=(n-ans*(ans-1)/2);
    printf("%lld\n",ans);
}
int main(){
    int t; cin>>t;
    while(t--){
        solve();
    }
}