回归预测 | MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测

news2024/11/17 12:52:55

回归预测 | MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测

效果一览

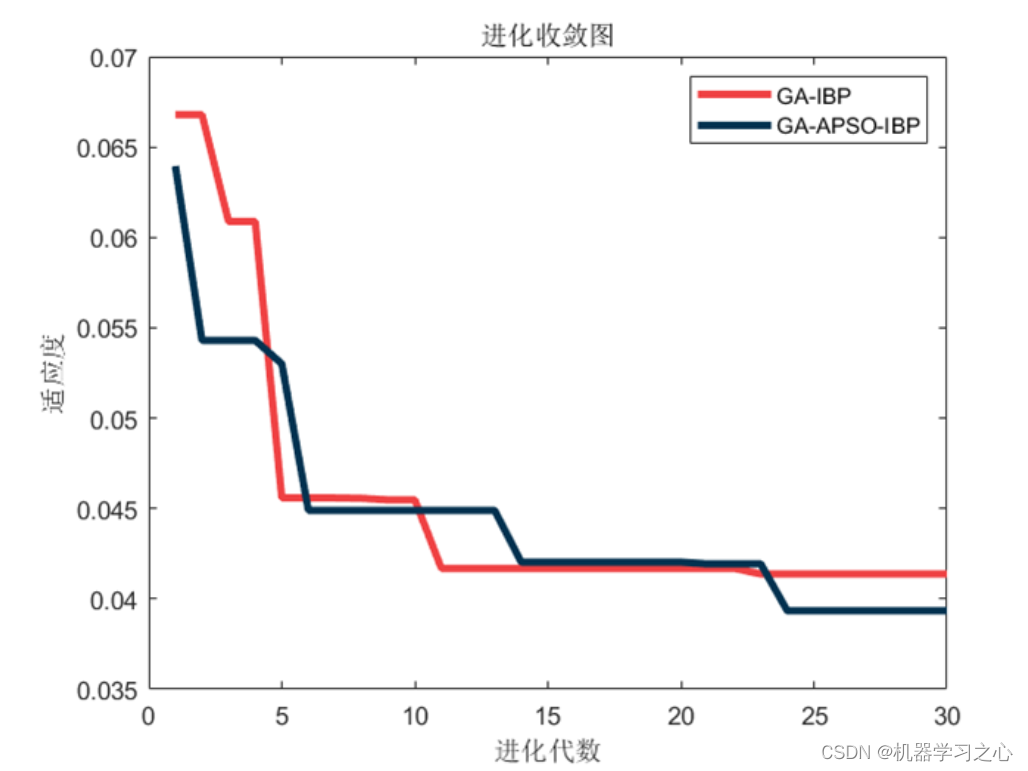
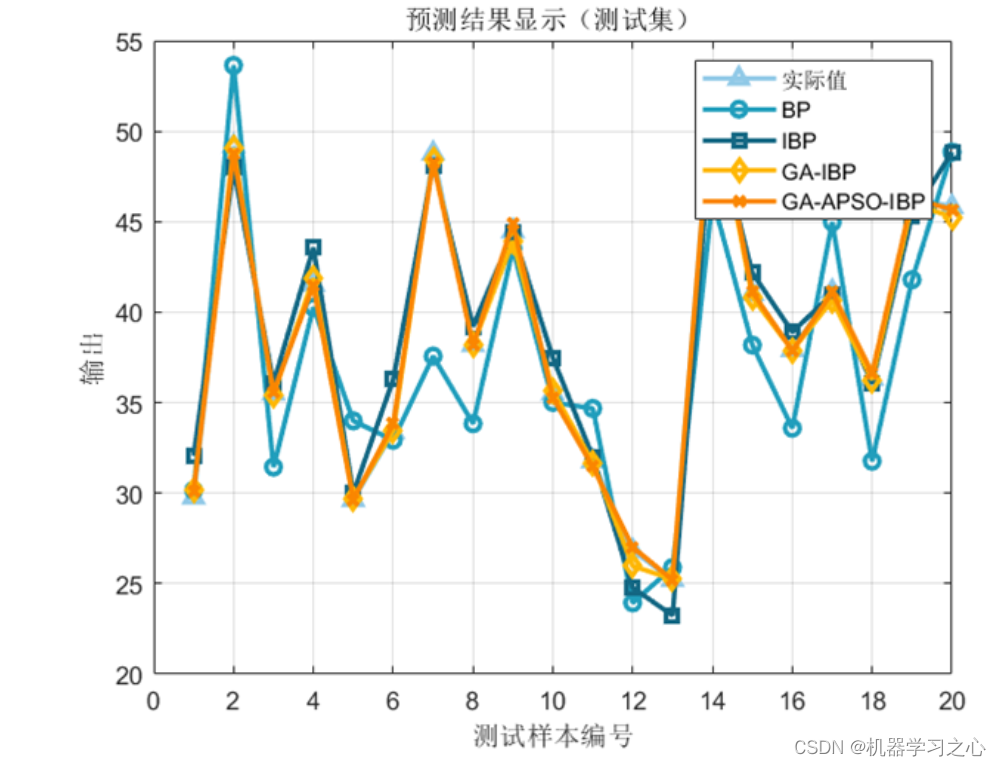
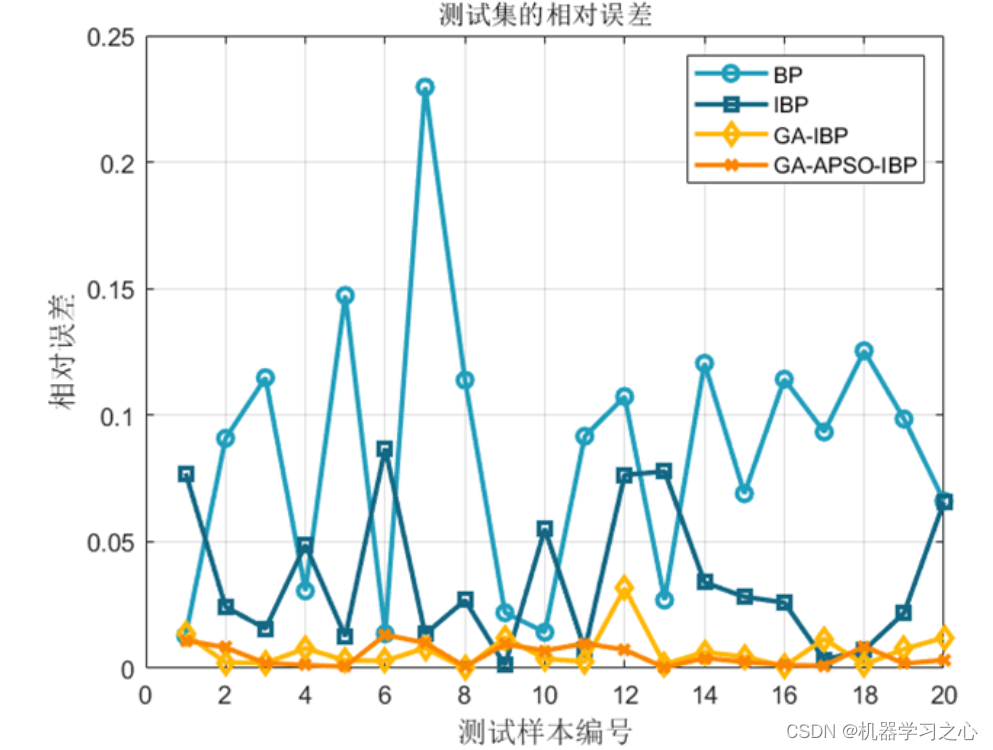
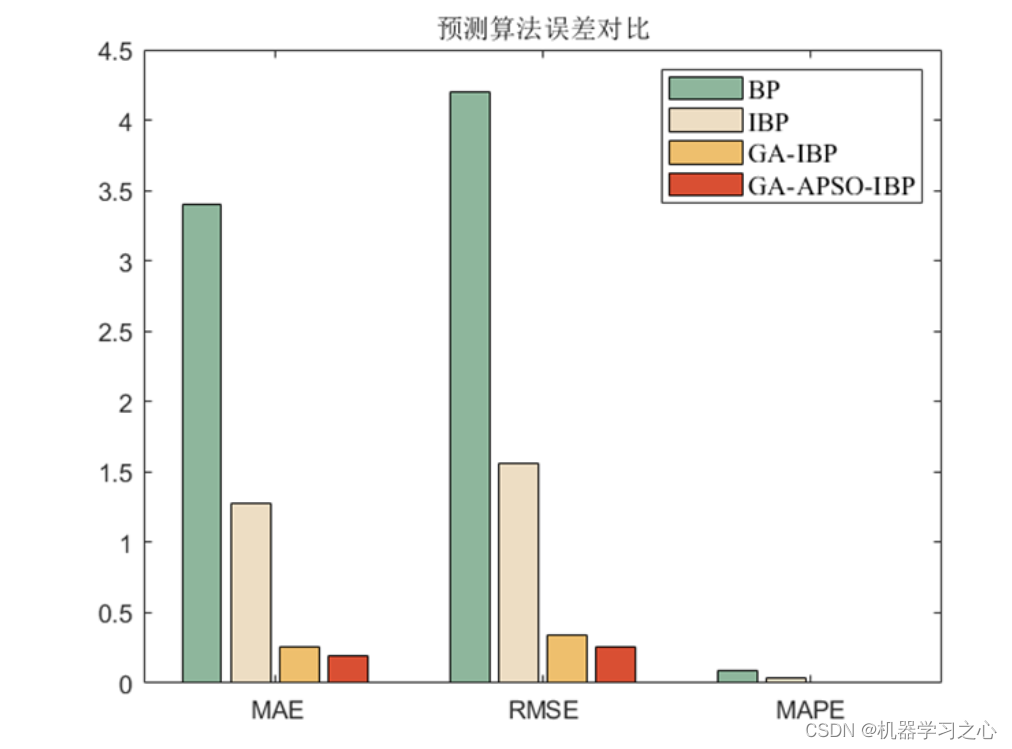
在这里插入图片描述

基本介绍

MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测；
程序包含：单隐含层BP神经网络、双层隐含层IBP神经网络、遗传算法优化IBP神经网络、改进遗传-粒子群算法优化IBP神经网络，结果显示改进的遗传-粒子群算法优化结果更佳。运行环境2018及以上。

模型描述

BP（Back-propagation，反向传播）神经网络是最传统的神经网络。也就是使用了Back-propagation算法的神经网络。请注意他不是时下流行的那一套深度学习。要训练深度学习level的网络你是不可以使用这种算法的。原因我们后面解释。而其实机器学习的bottleneck就是成功的突破了非常深的神经网络无法用BP算法来训练的问题。

程序设计

完整源码和数据获取方式：私信回复MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测（多指标，多图）。

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据
res = xlsread('data.xlsx');

%%  划分训练集和测试集
temp = randperm(103);

P_train = res(temp(1: 80), 1: 7)';
T_train = res(temp(1: 80), 8)';
M = size(P_train, 2);

P_test = res(temp(81: end), 1: 7)';
T_test = res(temp(81: end), 8)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);


%%  提取权值和阈值
w1 = pop(1 : inputnum * hiddennum);
B1 = pop(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = pop(inputnum * hiddennum + hiddennum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum);
B2 = pop(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);
 
%%  网络赋值
net.Iw{1, 1} = reshape(w1, hiddennum, inputnum );
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1}     = reshape(B1, hiddennum, 1);
net.b{2}     = B2';

%%  网络训练
net = train(net, p_train, t_train);

%%  仿真测试
t_sim1 = sim(net, p_train);
————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/129869457

%%  仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test);

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);



%%  相关指标计算
% 决定系数 R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

% 平均绝对误差 MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

% 平均相对误差 MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])