目录
参考文章:
代码主要内容:
主程序:
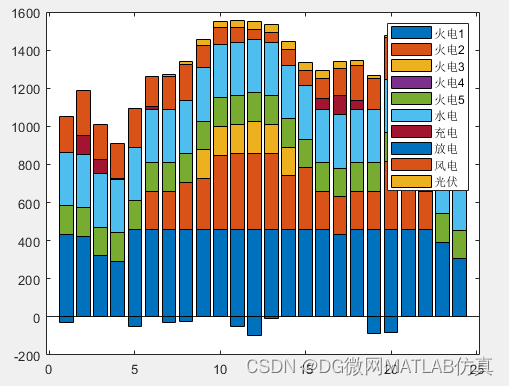
结果图:
参考文章:
考虑源荷两侧不确定性的含风电电力系统低碳调度——崔杨(2020)
代码主要内容:
参照考虑源荷两侧不确定性的含风电的低碳调度,引入模糊机会约束,程序包括储能、风光、火电机组及水电机组,解决了目标函数含有分类特征的约束问题、非线性约束/目标的线性转化问题,且考虑了机组的启停时间约束,目标函数考虑运行成本、弃风弃光和碳成本,有详细的资料,程序完整性好、模块化编程、注释清楚、方便学习!
主程序:
clc;clear all;
alfa=0.9;
pw=[188 237 188 181 204 156 174 186 118 89 77 54 52 80 82 107 144 185 163 221 215 240 223 190];
pv=[0 0 0 0 0 2.2000 5.5000 17.0000 28.6000 32.0000 39.0000 42.6000 42.0000 41.6000 40.5000 41.2000 36.5000 28.0000 16.0000 6.6000 1.1000 0 0 0];
pload=[945 845 745 780 998 1095 1147 1199 1300 1397 1449 1498 1397 1297 1197 1048 1000 1100 1202 1375 1298 1101 900 800];
Pgmin=[230 200 150 120 70]';%火电机组功率下限
Pgmax=[460 400 350 300 150]';%火电机组功率上限
Phmin=0;%水电下限
Phmax=280;%水电上限
rud=[240 210 150 120 70]';%火电爬坡
On_min=[8 7 6 4 3]';%开机时间
Off_min=[8 7 6 4 3]';%关机时间
a=1e-5.*[1.02 1.21 2.17 3.42 6.63]';%火电机组表格数据,下同
b=[0.277 0.288 0.29 0.292 0.306]';
c=[9.2 8.8 7.2 5.2 3.5]';
Sit=[25.6 22.3 16.2 12.3 4.6]';
e=[0.877 0.877 0.877 0.877 0.979]';
lam=[0.94 0.94 0.94 0.94 1.03]';
%储能参数
capmax=400;
EESmax=100;
EESmin=0;
socmax=0.9;
socmin=0.2;
theta=0.01;%自放电率
yita=0.95;
%-------------
w=50;d=100;tao=0.25;%碳交易价格、区间长度、增长幅度
Horizon=24;%时间参数
ngen=5;%火电机组数量
%% 决策变量
PG = sdpvar(ngen, Horizon);%火电
PH = sdpvar(1, Horizon);%水电
x_P_ch = sdpvar(1, Horizon);%充电
x_P_dis = sdpvar(1, Horizon);%放电
x_P_w = sdpvar(1, Horizon);%风电
x_P_v = sdpvar(1, Horizon);%水电
x_u_ch = binvar(1, Horizon);%充电状态
x_u_dis = binvar(1, Horizon);%放电状态
OnOff = binvar(ngen,Horizon);%火电机组状态
lin = sdpvar(1, Horizon);%目标3中间变量
%P的平方线性化参数
gn=5;
x_pf=sdpvar(ngen, Horizon);
gw1=sdpvar(gn+1,Horizon);
gw2=sdpvar(gn+1,Horizon);
gw3=sdpvar(gn+1,Horizon);
gw4=sdpvar(gn+1,Horizon);
gw5=sdpvar(gn+1,Horizon);
gw6=sdpvar(gn+1,Horizon);
gz1=binvar(gn, Horizon);gz2=binvar(gn, Horizon);gz3=binvar(gn, Horizon);gz4=binvar(gn, Horizon);gz5=binvar(gn, Horizon);
%模型构建
%% 约束条件生成
cons = [];
%火电机组
cons_gen = getConsGen1(PG,Pgmax,Pgmin,rud, Horizon,OnOff,On_min,Off_min);
cons = [cons, cons_gen];
%水电机组
cons = [cons, repmat(Phmin,1,Horizon)<=PH<=repmat(Phmax,1,Horizon)];
%储能约束
cons_ees = getConsEES(x_P_ch, x_P_dis, x_u_ch, x_u_dis, EESmax, EESmin, capmax, Horizon,theta);
cons = [cons, cons_ees];
%新能源出力约束
cons = [cons,0 <= x_P_w <=pw, 0 <= x_P_v <=pv];% ,0<= x_P_w+x_P_v+PH <=pload - sum(Pgmin)];
%功率平衡约束
ww=[0.6 1 1.4];
wv=[0.5 1 1.5];
wl=[0.9 1 1.1];
Pwb=((1-alfa)*ww(1)/2+ww(2)/2+ww(3)*alfa/2).*pw;
Pvb=((1-alfa)*wv(1)/2+wv(2)/2+wv(3)*alfa/2).*pv;
Plb=((1-alfa)*wl(1)/2+wl(2)/2+wl(3)*alfa/2).*pload;
%onoff*pg线性化出处理
yg = sdpvar(ngen,Horizon);
cons = [cons, yg <= PG, yg >= PG-repmat(Pgmax,1,Horizon).*(1-OnOff), repmat(Pgmin,1,Horizon).*OnOff <= yg <= repmat(Pgmax,1,Horizon).*OnOff];
%cons = [cons, (wl(2).*pload-ww(2).*x_P_w-wv(2).*x_P_v)+x_P_ch+x_P_dis-PH-sum(OnOff.*PG,1) == 0];
cons = [cons, (2-2*alfa).*(wl(2).*pload-ww(2).*x_P_w-wv(2).*x_P_v)+(2*alfa-1).*(wl(3).*pload-ww(1).*x_P_w-wv(1).*x_P_v)+x_P_ch+x_P_dis-PH-sum(yg) == 0];
%旋转备用约束
cons = [cons, (2-2*alfa).*(wl(2).*pload-ww(2).*x_P_w-wv(2).*x_P_v)+(2*alfa-1).*(wl(3).*pload-ww(1).*x_P_w-wv(1).*x_P_v)+x_P_ch+x_P_dis-PH-sum(OnOff.*repmat(Pgmax,1,Horizon))<=0];
%目标
%分段线性化
gn=5;
gl1=(Pgmax-Pgmin)./gn;
gl2=zeros(5,gn+1);
for i=1:5
gl2(i,:)=Pgmin(i):gl1(i):Pgmax(i);
end
cons = [cons, x_pf(1,:)==gl2(1,:).^2*gw1];
cons = [cons, x_pf(2,:)==gl2(2,:).^2*gw2];
cons = [cons, x_pf(3,:)==gl2(3,:).^2*gw3];
cons = [cons, x_pf(4,:)==gl2(4,:).^2*gw4];
cons = [cons, x_pf(5,:)==gl2(5,:).^2*gw5];
cons = [cons, gw1(1,:)<=gz1(1,:)];
for i=2:gn
cons = [cons, gw1(i,:)<=gz1(i-1,:)+gz1(i,:)];
end
cons = [cons, gw1(gn+1,:)<=gz1(gn,:)];
cons = [cons, sum(gz1)==ones(1,Horizon)];
cons = [cons, gw2(1,:)<=gz2(1,:)];
for i=2:gn
cons = [cons, gw2(i,:)<=gz2(i-1,:)+gz2(i,:)];
end
cons = [cons, gw2(gn+1,:)<=gz2(gn,:)];
cons = [cons, sum(gz2)==ones(1,Horizon)];
cons = [cons, gw3(1,:)<=gz3(1,:)];
for i=2:gn
cons = [cons, gw3(i,:)<=gz3(i-1,:)+gz3(i,:)];
end
cons = [cons, gw3(gn+1,:)<=gz3(gn,:)];
cons = [cons, sum(gz3)==ones(1,Horizon)];
cons = [cons, gw4(1,:)<=gz4(1,:)];
for i=2:gn
cons = [cons, gw4(i,:)<=gz4(i-1,:)+gz4(i,:)];
end
cons = [cons, gw4(gn+1,:)<=gz4(gn,:)];
cons = [cons, sum(gz4)==ones(1,Horizon)];
cons = [cons, gw5(1,:)<=gz5(1,:)];
for i=2:gn
cons = [cons, gw5(i,:)<=gz5(i-1,:)+gz5(i,:)];
end
cons = [cons, gw5(gn+1,:)<=gz5(gn,:)];
cons = [cons, sum(gz5)==ones(1,Horizon)];
cons = [cons, PG(1,:)==gl2(1,:)*gw1];
cons = [cons, PG(2,:)==gl2(2,:)*gw2];
cons = [cons, PG(3,:)==gl2(3,:)*gw3];
cons = [cons, PG(4,:)==gl2(4,:)*gw4];
cons = [cons, PG(5,:)==gl2(5,:)*gw5];
%乘积线性化
yy=binvar(ngen,Horizon);
cons = [cons, yy <= OnOff, yy <= (1-OnOff)];
C1=sum(sum(repmat(a,1,Horizon).*x_pf+repmat(b,1,Horizon).*PG+repmat(c,1,Horizon)+repmat(Sit,1,Horizon).*yy));
C2=sum(500.*(Pwb-x_P_w)+500.*(Pvb-x_P_v));
dd = binvar(3,Horizon);
for i=1:Horizon
%assign(lin(i),0);
ml(i)=sum(e.*PG(:,i));
mp(i)=sum(lam.*PG(:,i));
%lin(i)=w*(mp(i)-ml(i));
cons = [cons, sum(dd) == 1,
implies(dd(1,i), [ mp(i)<=ml(i)+d, lin(i) == w*(mp(i)-ml(i))]);
implies(dd(2,i), [ml(i)+d<=mp(i)<=ml(i)+2*d, lin(i) == (1+tao)*w*(mp(i)-ml(i))-tao*w*d]);
implies(dd(3,i), [mp(i)>=ml(i)+2*d, lin(i) == (1+2*tao)*w*(mp(i)-ml(i))-3*tao*w*d])];
end
C3=sum(lin);
f=C1+C2+C3;
%f=sum(x_P_w);
options = sdpsettings('verbose',2,'solver', 'cplex');
% options = sdpsettings('verbose',2);
sol = optimize(cons, f,options);
if sol.problem ~= 0
error("求解失败");
end
PG = value(PG);
PH = value(PH);
x_P_ch = value(x_P_ch);
x_P_dis = value(x_P_dis);
x_P_w = value(x_P_w);
x_P_v = value(x_P_v);
OnOff = value(OnOff);
tt=[PG(1,:);PG(2,:);PG(3,:);PG(4,:);PG(5,:);PH;x_P_ch;x_P_dis;x_P_w;x_P_v];
bar(tt','stack')
legend('火电1','火电2','火电3','火电4','火电5','水电','充电','放电','风电','光伏');
结果图: