【力扣】59. 螺旋矩阵 II

给你一个正整数 $n$ ，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的 $n\times n$ 正方形矩阵 $matrix$ 。

示例 1：

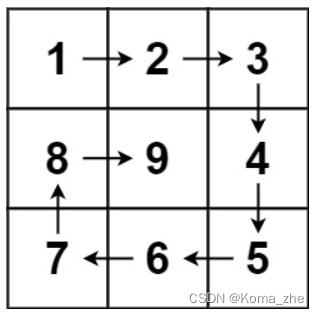
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：
输入：n = 1
输出：[[1]]

提示：
1 <= n <= 20

题解

注意每一循环一圈的时候，注意循环不变量原则

• 上行从左到右 (左闭右开)
• 右列从上到下 (左闭右开)
• 下行从右到左 (左闭右开)
• 左列从下到上 (左闭右开)

public class Main {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        // 定义每循环一个圈的起始位置
        int startx = 0, starty = 0;
        // 每个圈循环几次，例如 n为奇数 3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int loop = n / 2;
        // 矩阵中间的位置，例如：n为 3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int mid = n / 2;
        // 用来计数赋值
        int count = 1;
        // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int offset = 1;
        int i, j;

        while ((loop--) > 0) {
            i = startx;
            j = starty;

            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < n - offset; j++) {
                res[i][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 1;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if ((n % 2) == 1) {
            res[mid][mid] = count;  //res[startx][starty] = count;
        }
        return res;
    }
}