
clc
clear
close all
% 参数设置
TBP = 80; % 时间带宽积
T = 10e-6; % 脉冲持续时间
N_ZD = 60; % 零频点位于中点右侧的距离,P58
% 参数计算
B = TBP/T; % 信号带宽
K = B/T; % 线性调频频率
alpha_os = 5; % 过采样率
F = alpha_os*B; % 采样频率
N = 2*ceil(F*T/2); % 采样点数
dt = T/N; % 采样时间间隔
t_c = N_ZD*dt; % 脉冲时间偏移
% 变量设置
t = -T/2:dt:T/2-dt; % 时间变量
% 信号表达
st1 = exp(1j*pi*K*(t-t_c).^2); % 有时间偏移的chirp信号
st2 = zeros(1,N); % 等长的空信号
st = [zeros(1,40),st1,st2,st1,st2,st1,zeros(1,40)];
N_st = length(st); % 信号长度
Sf = fftshift(fft(st)); % 信号频域表达式
f = -F/2:F/N_st:F/2-F/N_st; % 频率变量
n = 0:N_st-1; % 采样点
% 窗函数
window_1 = kaiser(N,2.5)'; % 时域窗函数
Window_1 = fftshift(window); % 频域窗函数
% 匹配滤波——方式1
ht_1 = conj(fliplr(st1)); % 将时间反褶后的复制脉冲取复共轭
%ht_window_1 = window_1.*ht_1; % 加窗的时域匹配滤波器表达式
Hf_1 = fftshift(fft(ht_1,N_st)); % 补零离散傅里叶变换
Sf_out_1 = Sf.*Hf_1; % 频域输出
st_out_1 = ifft(ifftshift(Sf_out_1)); % 时域输出
% 匹配滤波——方式2
ht_2 = st1; % 复制脉冲
Hf_2 = conj(fftshift(fft(ht_2,N_st))); % 补零后离散傅里叶变换后复共轭
Sf_out_2 = Sf.*Hf_2; % 频域输出
st_out_2 = ifft(ifftshift(Sf_out_2)); % 时域输出
plot(abs(st_out_2))
% 匹配滤波——方式3
window_3 = kaiser(N_st,2.5)'; % 信号长度的窗函数
Window_3 = fftshift(window_3); % 频域窗函数
Hf_3 = Window_3.*exp(1j*pi*f.^2/K); % 匹配滤波器频域表达式
Sf_out_3 = Sf.*Hf_3;
st_out_3 = ifft(ifftshift(Sf_out_3));
% 绘图
subplot(411),plot(n,real(st)),axis([0 N_st,-1.2 1.2])
subplot(412),plot(n,abs(st_out_1)),xlim([0,N_st])
subplot(413),plot(n,abs(st_out_2)),xlim([0,N_st])
subplot(414),plot(n,abs(st_out_3)),xlim([0,N_st]) 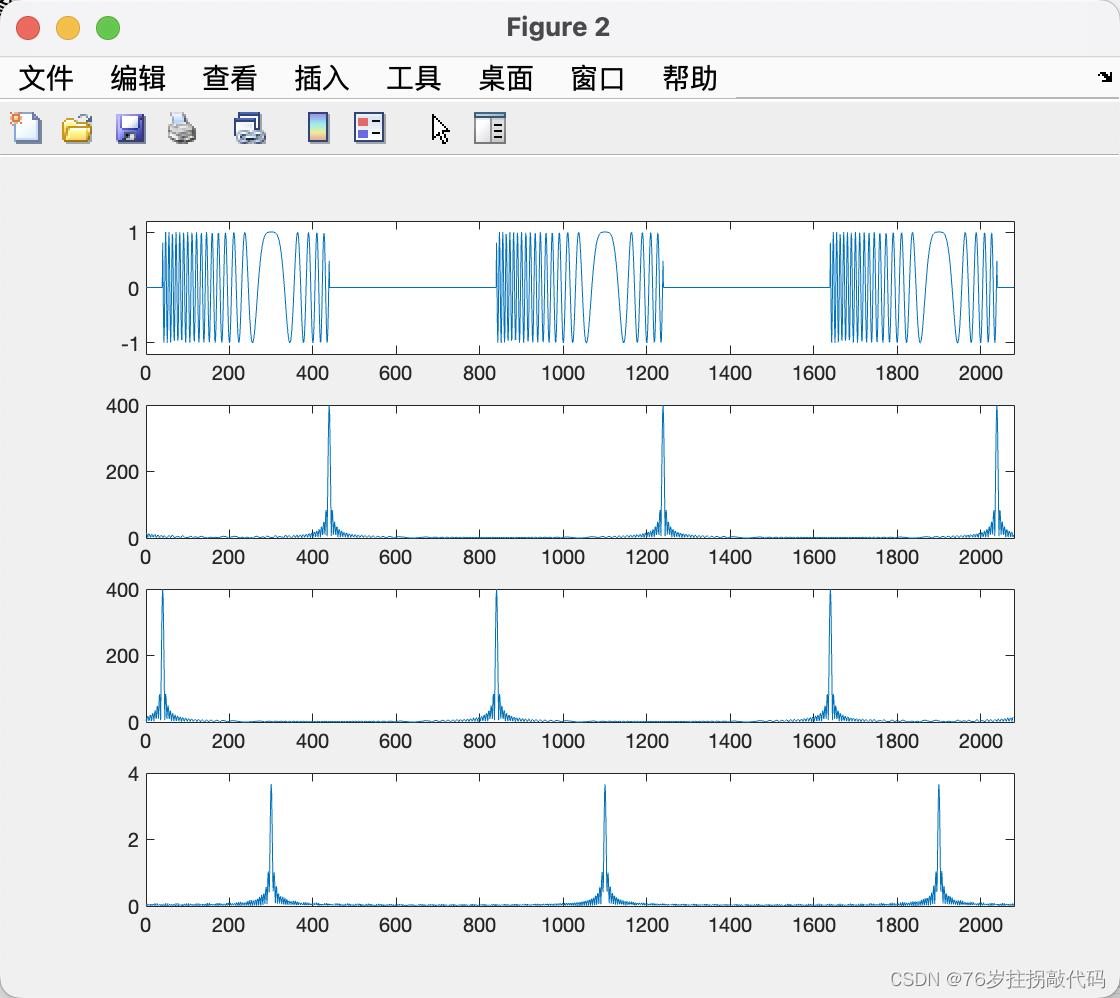
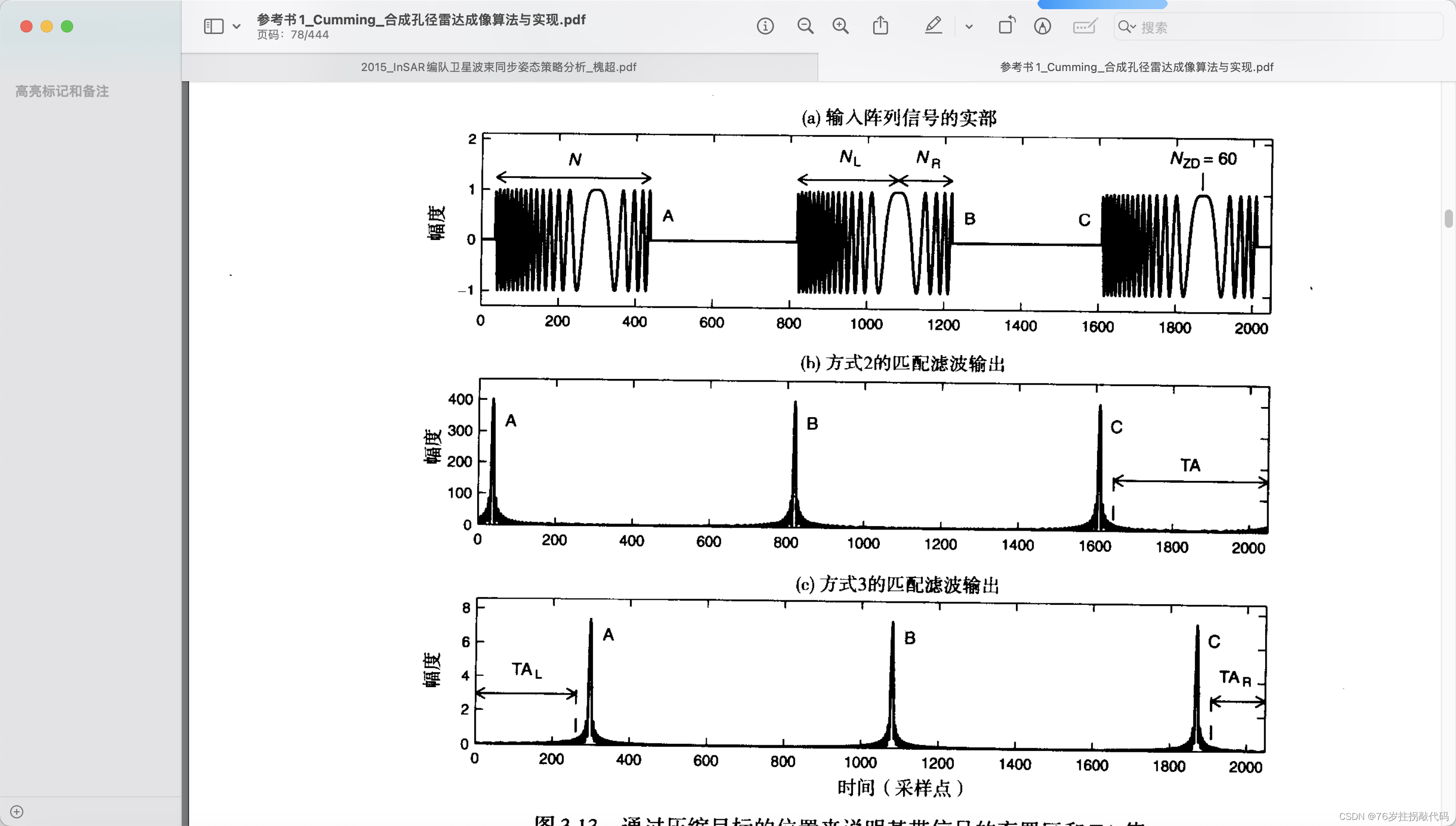
可以看到方式一脉冲压缩至输入序列的后沿,方式二脉冲压缩至输入序列前沿,方式三脉冲压缩至零频位置