摘要:通过设置时分复用(TDMA)波形结合FMCW毫米波雷达仿真获取目标的距离、速度和方位角3D点云信息。在本案例中,首先通过发射天线交替发射FMCW波形并通过接收天线依次接收回波信号从而得到雷达原始数据,其次对获取的原始数据依次经行距离、速度、角度估计从而输出目标的3D点云。阅读本文档,你将对TDMA-MIMO雷达的基本原理、毫米波雷达距离估计、速度估计以及角度估计的基本原理有所了解,另外CA-CFAR恒虚警以及MUSIC-DOA估计在本案例中也有所涉及。
1 TDMA-MIMO原理
时分复用(TDMA)的应用在多发射多接收天线(MIMO)的毫米波雷达中是一种常用的波形,它的实现方式也比较简单,即通过不同的发射天线交替发射chirp信号,在接收端依次接收来自目标反射的回波信号。例如:使用Ntx个发射天线和Nrx个接收天线的MIMO雷达,可以合成Ntx*Nrx个虚拟接收天线。如下图所示:
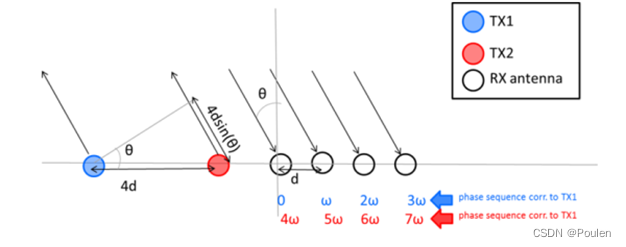

图中假设FMCW雷达采用2个发射天线和4个接收天线的工作模式,接收天线间的间距d=λ/2,其中λ表示波长。两个发射天线间距为4d,因此发射天线依次发射chirp信号,这时可以将2发4收的工作模式等效为1发8收的工作模式。
假设静止目标位与接收天线水平方向的夹角为θ,这时相邻天线这间的相位变化可以表示为:
![]()
若目标不是静止,在采用TDMA波形时,由于发射天线2相较于发射天线1有一个chirp周期的时间延迟,这时为了能够正确的估计目标的方位角,需要对这个延迟相位进行补偿,通常也把这个延迟相位叫做由于速度引起的多普勒模糊。


对于发射天线数Ntx=2,接收天线数Nrx=4的情况,假设在8根虚拟天线(Ntx*Nrx=8)上对应目标的2D-FFT结果序列为X(m,n),其中m表示这个2D-FFT结果对应的发射天线编号(0<m≤Ntx-1),n表示这个2D-FFT结果对应的接收天线编号(0<n≤Nrx-1),那么多普勒相偏补偿可通过下式进行完成:
![]()
2 信号建模
假设雷达发射调频连续波信号,此时发射信号的复信号表示为(实际上雷达都是发射实信号,后续通过正交采样完成复信号的转变):
![]()
式中A表示信号振幅,fc表示信号的载频,μ=Bw/Tc表示调频斜率,Bw为带宽,Tc为chirp持续时间,t表示快时间。雷达的回波信号为发射信号的一个时延版本,表示为:
![]()
式中τ表示时延,由目标也雷达的距离决定。雷达接收的回波信号与发射信号进行混频、过低通滤波器得到中频信号:
![]()
根据式(7)可知,对快时间t进行FFT变换,可以提取到信号的中心频率:
![]()
对于静止距离雷达为R的目标而言,此时τ=2/Rc,c表示光速。结合式(8)可估计目标的距离:
![]()
考虑到MATLAB采样率有限的问题,在建立仿真模型时直接从中频信号入手。前面提到,回波时延包含了目标的距离速度信息,假设初始距离为R0处有一目标以速度Vr运动,此时目标目标的距离随时间变化的关系为:
![]()
式中n和m分别表示快慢时间采样编号,fs表示快时间采样率。考虑到快时间(一个chirp采样时间)内速度对距离变化的影响不大,于是式(10)可以简化为:
![]()
于是时间延迟可以用下式表示:
![]()
因此,在MATLAB中,我们可以建立信号模型为:
![]()
将式(12)代入其中,就可以获得一张2维包含目标距离速度信息的回波矩阵。为了实现目标方位角度的测算,我们需要增加一个天线维度来生成一个数据原始立方。因此我们只需要在不同通道间加入相位信息,即可完成三维数据立方的建模。由前所述,为了在中频信号中引入方位信息,只需要在式(13)的基础上加入式(1)即可获得包含目标距离、速度和方位角度的原始信号模型:
![]()
此外,为了体现TDMA方案中由速度引起的多普勒时延,在仿真时需要加入多普勒相偏,于是上式可以从新表述为:
![]()
式中txId和rxId表示发射天线编号和接收天线编号,其中0<txId≤2,0<rxId≤4,numrx表示接收天线数量。至此,关于TDMA模型信号的MATLAB建模已经完成,此外为了更接近真实雷达的收发模式,我们还可以设置接收多个帧模式。因此设置3个目标,距离、速度和方位角分别为(10m,-2.2m/s,30°)、(5m,4.4m/s,-15°)、(22,3.5,13°)的MATLAB信号建模的代码如下所示:
snr = 10; %信噪比
rawdata = zeros(numsamples,numchirp,numrx * numtx ,numframe); %创建四维数组用以填充雷达原始数据
fastsampdata = zeros(numsamples,1); %临时存放的快时间采样数据空间
for frameid = 1 : numframe
for txid = 1 : numtx
for rxid = 1 : numrx
for chirpid = 1 : numchirp
for targetid = 1 : numtarget
for sampleid = 1 : numsamples
R = target(targetid,1) + ((chirpid-1)*T)*target(targetid,2) + (frameid-1)*numchirp*T*target(targetid,2); %计算目标随速度变化的距离,以忽略快时间对距离的影响
delay = 2 * R / parameter.c;
fixphase = exp(1j*2*pi*(f0*delay-0.5*slope*delay^2)); %中频信号的固定相位,末尾的相位为剩余视频相位,为了更真实还原毫米波雷达数据,本程中没有将其省略
fastsampdata(sampleid) = abs(randn)^2 * exp(1j*2*pi*slope*delay*t(sampleid)) * fixphase; %这里采用随机起伏
end
Detadoppler = 2*pi*(2 * target(targetid,2) / lambda)*T/2; %值得注意的是天线交替工作,因此由于发射天线2相对于发射天线1多了T/2的延迟
azimuthphase = exp(1j*(2*pi/lambda)*sind(target(targetid,3)) * ( (rxid -1) * Detarx + (txid - 1) * Detatx) ) * exp(1j*(txid-1)*Detadoppler); %目标方位角信息
rawdata(:,chirpid,(txid-1)*numrx + rxid,frameid) = rawdata(:,chirpid,(txid-1)*numrx + rxid,frameid) + fastsampdata.* azimuthphase;
end
end
%加入高斯噪声
MixIQ = rawdata(:,:,(txid-1)*numrx + rxid,frameid);
xigema = std(MixIQ)/db2mag(snr);
MixIQ = MixIQ + ((randn(size(MixIQ)) + 1i*randn(size(MixIQ)))).*xigema;
rawdata(:,:,(txid-1)*numrx + rxid,frameid) = MixIQ;
end
end
end在上述建模中建立一个四维数组用来存储原始数据,维度依次代表快时间采样、chirp数、天线数以及帧数。绘制时域波形代码和时域波形如下所示:
%%展示时域信号波形
timedomian = squeeze(rawdata(:,10,5,1));
figure;
subplot(2,1,1);
plot(real(timedomian),'Color',[0 0 0],'LineWidth',1.2);
title('原始信号时域波形(实部)');
ylabel('信号幅度');
xlabel('时域采样点');
xlim([0 512]);
subplot(2,1,2);
plot(imag(timedomian),'Color',[0 0 0],'LineWidth',1.2);
title('原始信号时域波形(实部)');
ylabel('信号幅度');
xlabel('时域采样点');
xlim([0 512]);
clear timedomian;

3 距离速度估计(RD图)
根据上述建立的模型,可以获取一个四维的原始数据。分别对快时间和慢时间进行FFT并对不同通道以及不同帧进行循环。具体实现代码如下所示:
numsample = parameter.numsmaple;
numchirp = parameter.numchirp;
numframe = parameter.numframe;
numtx = parameter.Txnum;
numrx = parameter.Rxnum;
rangedoppler = zeros(numsample,numchirp,numtx*numrx,numframe); %创建预定空间
%距离fft
for frameId = 1:numframe
for channalId = 1:numtx*numrx
for chirpId = 1 : numchirp
temp =squeeze(rawdata(:,chirpId,channalId,frameId)).*hamming(numsample); %加窗
rangedoppler(:,chirpId,channalId,frameId) = fft(temp);
end
end
end
%速度fft
for frameId = 1:numframe
for channalId = 1:numtx*numrx
for sampleId = 1 : numsample
temp =squeeze(rangedoppler(sampleId,:,channalId,frameId)).*hamming(numchirp).'; %加窗
rangedoppler(sampleId,:,channalId,frameId) = fftshift(fft(temp));
end
end
end此外,由于单个通道的脉冲能量有限,为了提高系统的鲁棒性,采用非相干脉冲积累技术沿着通道维度经行非相干叠加,代码实现过程如下:
mulaccumulata = zeros(numsample,numchirp,numframe);
for frameId = 1: numframe
for channalId = 1 : numtx*numrx
mulaccumulata(:,:,frameId) = mulaccumulata(:,:,frameId) +
abs(rangedoppler(:,:,channalId,frameId));
end
end对叠加后的2DFFT结果进行可视化结果如下:


图4中出现了3个峰值,它们分别代表了每个目标出现的位置。可以看出估计值与实际值非常接近,读取峰值所在的索引坐标即可得到目标的距离和速度信息。
4 自动检测技术
在得到2DFFT结果之后,我们不可能人为的去读取峰值对应的索引值来进行后续处理,所以我们需要采用恒虚警(CFAR)处理技术进行目标筛选。常用的CFAR检测器分为均值类、有序统计类,有效的选择CFAR检测器可以提高系统的鲁棒性。为了减少文章篇幅,这里不在累赘CFAR基本原理,在这里我们选择了CACFAR检测器进行检测,由于经过CACFAR检测的单个目标并不单单包含一个点,而是它附近的点都会被记录下来。因此经过CACFAR后,我们需要筛选出它们之间的最大值作为最终的目标,并将最大值所在的索引值进行记录。
对上述2DFFT执行CACFAR后输出如下:

从图5中可以非常清晰的分辨出3个目标,通过索引筛选,输出距离和速度对应的索引如下所示:

值得注意的是,在图6中第三维度代表不同的相邻帧。可以看到在经过CACFAR处理技术以及最大值选取后可以较准确的自动输出目标所在距离和速度索引。
5 方位角估计
方位角度估计也叫DOA估计,常用的方法有3DFFT、Capon、Music算法。对于MUSIC算法,在到达波源属于非相干波源时,有很好的估计效果,当来波是相干波源时,性能急剧恶化,考虑到上述问题,在本Demo中,我采用空间平滑技术改进MUSIC算法。此外还分辨研究了做多普勒补偿和未作多普勒补偿的区别。
未作多普勒补偿前空间平滑MUSIC算法代码实现过程以及结果可视化如下:
%% 任意提取距离-方位切片数据进行DOA估计
RangeAziSlicData(:,:) = squeeze( rawdata(:,10,:,frameID) );
%% 考虑到相关源,这里采用空间前向平滑MUSIC算法
SubArrayData = RangeAziSlicData(:,1:SubNum).';
Rf = (1/numsample) * SubArrayData *conj(SubArrayData.');
for i = 2:L
SubArrayData = RangeAziSlicData(:,i:SubNum+ i -1).';
Rf = Rf + (1/numsample) * SubArrayData *conj(SubArrayData.');
end
Rf = 1/L * Rf ; %前向协方差矩阵
[V,D] = eig(Rf); %特征值分解
EVA = real(diag(D)');
[~,I] = sort(EVA);
V=V(:,I);
Un = V(:,1:end-numtarget);
P_Music = zeros(1,length(scale));
idx = 1;
for i=scale
a = exp(1j*2*pi/lambda*DetaAntannat(:)*sind(i));
P_Music(idx) = 1/( conj(a.')*Un*conj(Un.')*a );
idx = idx + 1;
end
targetdoa(:,frameID) = P_Music; %未补偿前DOA估计图谱

观察图7发现,未作多普勒补偿前虽然可以分辨出3个目标,但是其估计的方位角度与实际角度误差较大,导致估算不准确。因此,在采用TDMA方案估计角度时,必须先对多普勒模糊进行补偿,该实现的代码步骤以及输出结果如下所示:
for targetid = 1 : numtarget
rangetempindex = tagetestindex(1,targetid,frameID);
dopplertempindex = tagetestindex(2,targetid,frameID);
estv = dopplerindex(dopplertempindex); %获取目标估计速度
Detadoppler = 2*pi*(2 * estv / lambda)*T; %计算多普勒补偿相位
RangeAziSlicData(:,:) = squeeze( rangedoppler(rangetempindex,:,:,frameID) );
for rxid = 1 : numrx
RangeAziSlicData(:,rxid + numrx) = RangeAziSlicData(:,rxid +
numrx).*exp(-1j*Detadoppler);
end
SubArrayData = RangeAziSlicData(:,1:SubNum).';
Rf = (1/numchirp) * SubArrayData *conj(SubArrayData.');
for i = 2:L
SubArrayData = RangeAziSlicData(:,i:SubNum+ i -1).';
Rf = Rf + (1/numchirp) * SubArrayData *conj(SubArrayData.');
end
Rf = 1/L * Rf ; %前向协方差矩阵
[V,D] = eig(Rf); %特征值分解
EVA = real(diag(D)');
[~,I] = sort(EVA);
V=V(:,I);
Un = V(:,1:end-1);
P_Music = zeros(1,length(scale));
idx = 1;
for i=scale
a = exp(1j*2*pi/lambda*DetaAntannat(:)*sind(i));
P_Music(idx) = 1/( conj(a.')*Un*conj(Un.')*a );
idx = idx + 1;
end
esttargetdoa(:,frameID) = esttargetdoa(:,frameID) + P_Music.'; %多普勒相偏补偿输出
end
从图8中可以看到,进行多普勒补偿后估计的方位角与设定的仿真基本一致。但是这里又出现了一个问题,我们应该如何将这些角度与相对应的目标进行匹配。在这里我们通过计算距离-方位角图来进行匹配,该实现过程如下所示:
%% 获取距离-方位角热图
for sampleid = 1 : numsample
ChilrpAziSlicData(:,:) = squeeze( rangedoppler(sampleid,:,:,frameID) );
%% 多普勒补偿
dopplercompentiontemp = find(tagetestindex(1,:,frameID)==sampleid);
if(~isempty (dopplercompentiontemp))
estv = dopplerindex(tagetestindex(2,dopplercompentiontemp,frameID));%获取目标估计速度
Detadoppler = 2*pi*(2 * estv / lambda)*T; %计算多普勒补偿相位
for rxid = 1 : numrx
ChilrpAziSlicData(:,rxid + numrx) = ChilrpAziSlicData(:,rxid + numrx).*exp(-1j*Detadoppler);
end
end
SubArrayData = ChilrpAziSlicData(:,1:SubNum).';
Rf = (1/numchirp) * SubArrayData *conj(SubArrayData.');
for i = 2:L
SubArrayData = ChilrpAziSlicData(:,i:SubNum+ i -1).';
Rf = Rf + (1/numsample) * SubArrayData *conj(SubArrayData.');
end
Rf = 1/L * Rf ; %前向协方差矩阵
[V,D] = eig(Rf); %特征值分解
EVA = real(diag(D)');
[~,I] = sort(EVA);
V=V(:,I);
Un = V(:,1:end-1); %默认一个距离单元存在一个目标
P_Music = zeros(1,length(scale));
idx = 1;
for i=scale
a = exp(1j*2*pi/lambda*DetaAntannat(:)*sind(i));
P_Music(idx) = 1/( conj(a.')*Un*conj(Un.')*a );
idx = idx + 1;
end
RangeAzi(sampleid,:,frameID) = P_Music; %生成伪谱距离角度
end距离-方位角图可视化如下:

通过图九我们得到方位角与距离的关联,因此根据这一关系很容易的将它们匹配起来。
6 3D点云生成
通过上述的处理之后,接下来就是生成可视化的点云图,方便用户查看目标或者后续的数据处理,例如目标航迹跟踪、聚类等等。实现的代码如下:
%% 绘制3D点云散点图(在该散点图中仅展示第一帧的图像信息)
figure;
X = parameter.rangeindex(pointcloud(1,:,1));
Y = parameter.dopplerindex(pointcloud(2,:,1));
Z = parameter.scale(pointcloud(3,:,1));
S = 50;
C = [0 1 0; 1 0 0; 0.5 0.5 0.5]; %注意:这是三个点目标是的RGB原组,若要改变目标数量,该原组需要改变
get = scatter3(X,Y,Z,S,C);
xlim([0 parameter.rangeindex(end)]);
xlabel('距离(m)');
ylim([parameter.dopplerindex(1) parameter.dopplerindex(end)]);
ylabel('速度(m/s)');
zlim([parameter.scale(1) parameter.scale(end)]);
zlabel('角度(°)');
title('3D点云图');
view(30,35);
%% 控制台输出估计目标的三维信息(仅展示第一帧捕获的信息)
disp('估计目标距离、速度、方位角如下列表所示:');
for targetid = 1 : size(pointcloud,2)
disp(['目标 ' num2str(targetid) ':']);
range = parameter.rangeindex(pointcloud(1,targetid,1));
Estv = parameter.dopplerindex(pointcloud(2,targetid,1));
doa = parameter.scale(pointcloud(3,targetid,1));
disp(['( ' num2str(range) ',' num2str(Estv) ',' num2str(doa) ' )']);
end可视化结果如下:

控制台输出目标信息如下:

在图8的点云中每个目标只有一个点在实际中往往是不可取不太可能的,通常情况下每个目标或多或少都会识别出超过1个以上的点云,由于博主为了让读者更好的理解,在CFAR自动检测时就已经将多余的点云信息滤除掉,只保留了最大值对应的点云。从图8可以看到,估计的距离-速度-角度与实际值相差甚微。
7 总结
本文仅供参考,如有不足之处望各位看官老爷即使指出,另外写文不易,望多支持支持。









![SQL 错误 [22007]: ERROR: invalid input syntax for type date: ““](https://img-blog.csdnimg.cn/d13f5e3b10724faf986fa97c8952d583.png#pic_center)