在这篇论文核心:
- 实现了dso的点线优化框架
- 实现了线特征的参数最小化
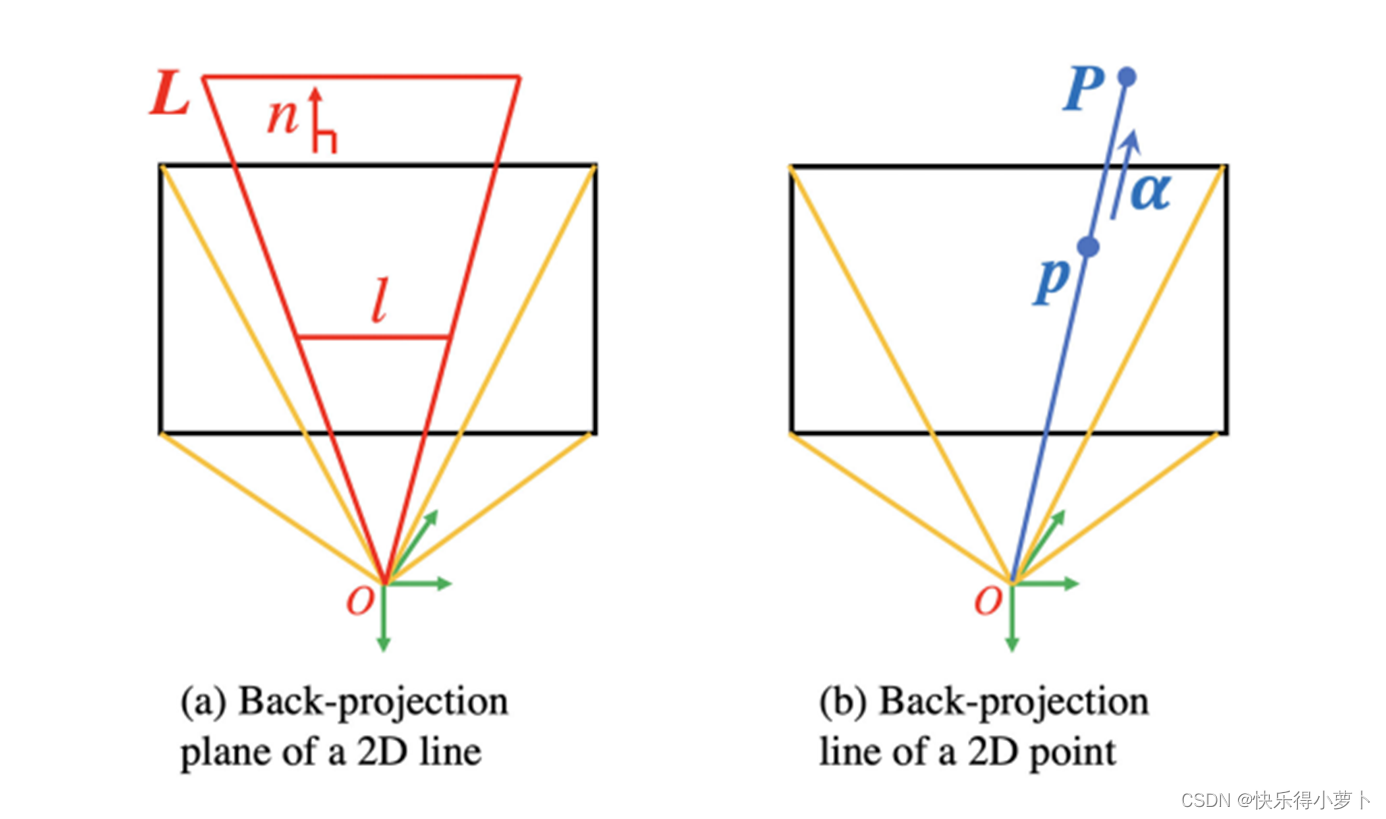
点的投影与线的投影
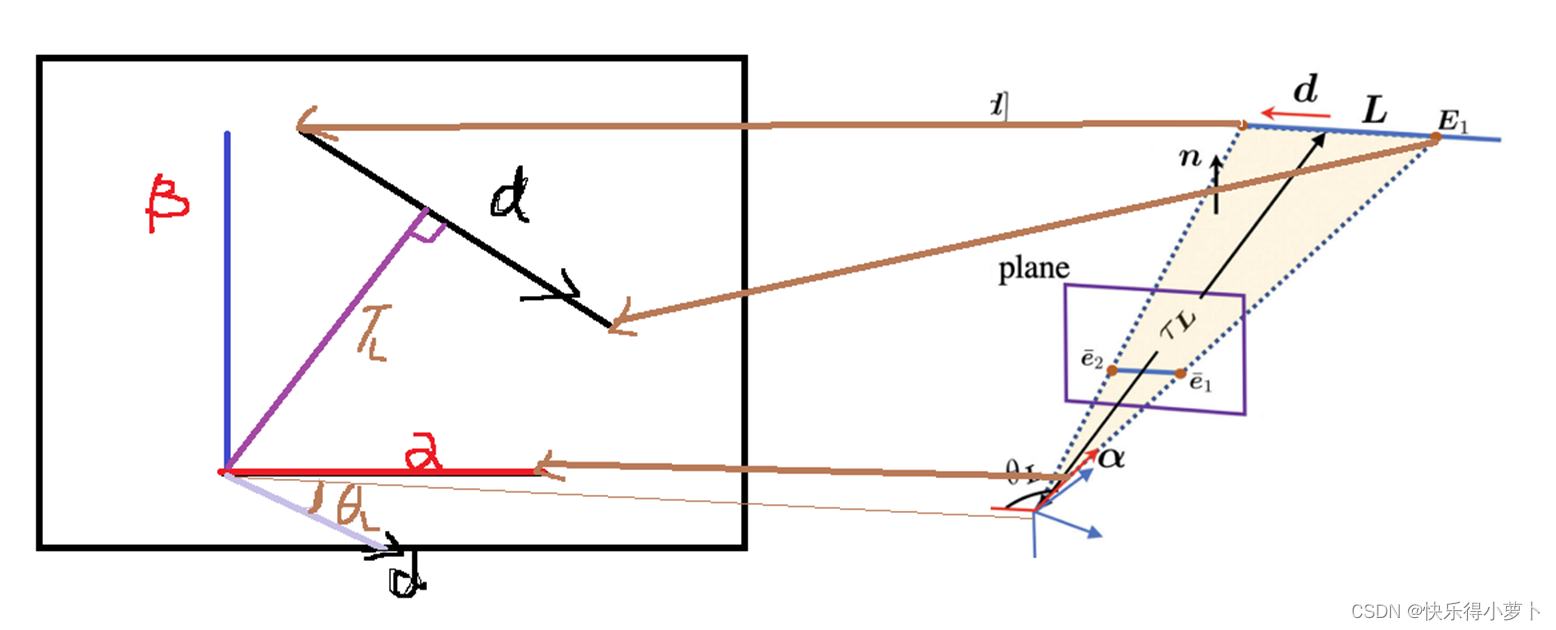
点在相机中是一个射线的投影,线其实是一个平面的投影。在vins等系统中采用逆深度对点特征进行表达,三维点只需要一维度的表达就可以了,大大减小了优化参数,同时个人认为少的参数在数据量小的时候是很好的,比如只有两帧优化深度用逆深度好。同样图像在平面中检测到线特征后其实已经有一部分已经是包含约束的了,在左图中l直线是L平面中的很多直线的投影,也就是真实的3d直线是在L这个二维平面中的,那么很自然一个在二维平面的线仅仅 具有2个优化参数,也就是说可以对两个参数进行优化得到3d线。
2维参数表达
普吕克坐标系参数如左图所示,其参数为m、d一共是6个数字,其中m和d也是存在约束关系的。因此有的SLAM系统会把普吕克坐标系下的线参数转换成SO3SO2的形式,这样就化成了4个参数的优化问题,把带约束的优化转换成无约束的优化。上面铺垫了2个参数约束的好处,因此主要说明2个参数优化出线特征,其思想如右图所示。
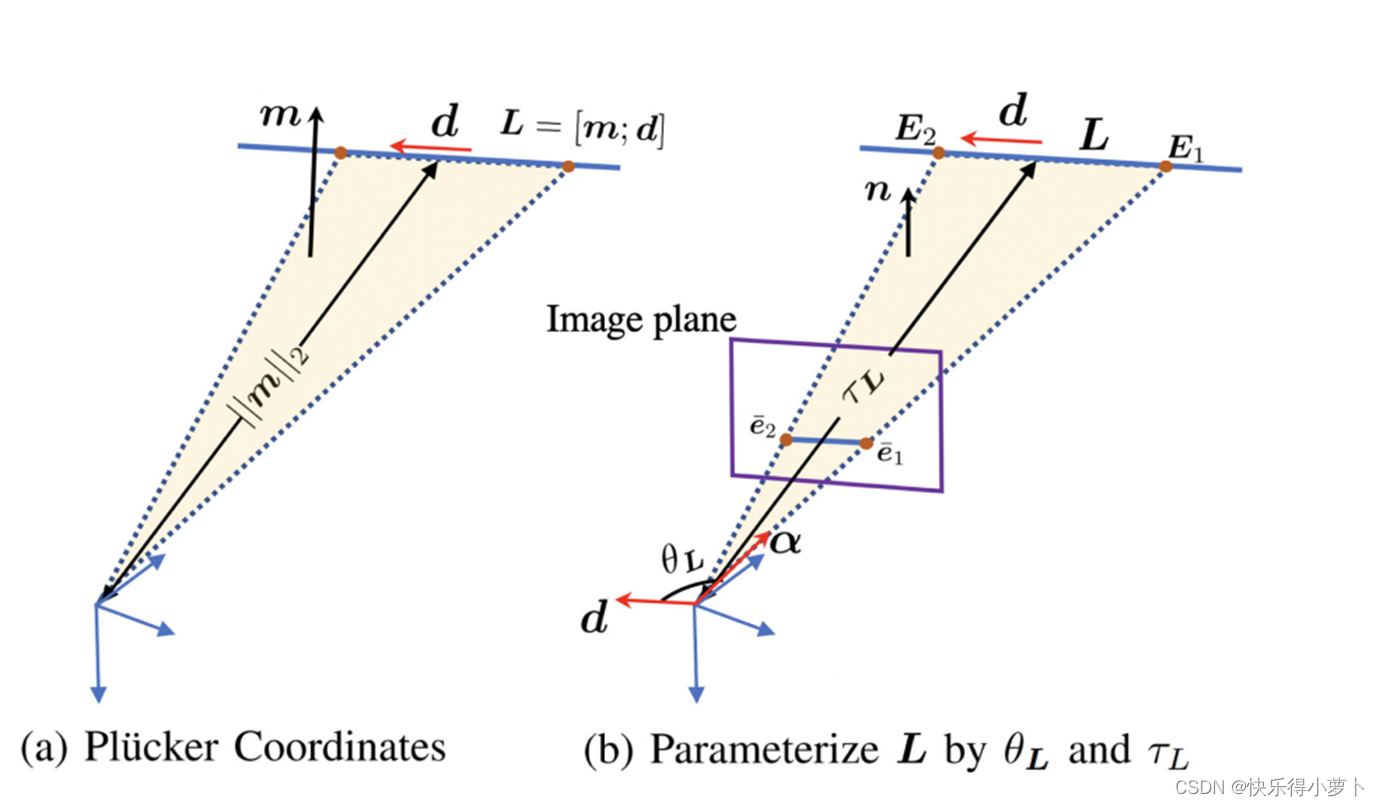
右图其实是很清晰的,d是3d线的方向,e_1 e_2是线在图像平面的坐标点、n是平面的坐标点。核心理解是构建平面,也就是在oE1E2二维平面里进行优化,构建的坐标轴是 allpa 以及 allpan 也就是在平面中与allpa垂直的一条单位向量,在这个二维坐标系中构建线其实就是角度(1维度)和距离(1维度),方向向量在坐标系下的表示自然是sin cos的形式。下面这个图,左边是右边对应平面的展开图,棕色的线代表对应关系(不过d画反了,凑合看吧)。
原论文中的公式: