目录
1 行列式和矩阵的比较
2 简单总结矩阵与行列式的不同
3 加减乘除的不同
3.1 加法不同
3.2 减法不同
3.3 标量乘法/数乘
3.3.1 标准的数乘对比
3.3.2 其他数乘对比
3.4 乘法
4 初等线性变换的不同
4.1 对矩阵进行线性变换
4.2 对行列式进行线性变换呢?
1 行列式和矩阵的比较
- 如果矩阵行数列数相等,那么这个矩阵是方阵,只有方阵才有行列式
- 行列式必须是行列数相等。
- 行列式是方阵的一种特殊运算,加减乘除规则都和矩阵不同
2 简单总结矩阵与行列式的不同
- 区别1
- 矩阵是一个n*m的数表 矩阵是多个向量 ; 矩阵的行数和列数可以不同;
- 行列式是一个n阶的方阵;
- 区别2
- 矩阵不能从整体上被看成一个数, 矩阵是多个向量 ;
- 行列式最终可以算出来变成一个数;
- 区别3
- 加法不同
- 减法不同
- 数乘不同
- 乘法完全不同,不可比
- 区别4
- 线性变化的交换,行列式不同
- 线性变化的倍数,行列式不同
- 线性变化的倍加,行列式不变,是相同的
3 加减乘除的不同
3.1 加法不同
- 矩阵加法,两个矩阵都是n*m,A+B = 对应元素相加
- 行列式加法,两个矩阵都是n*m,A+B = 对应元素相加
3.2 减法不同
- 减法的差别,参考加法
3.3 标量乘法/数乘
3.3.1 标准的数乘对比
- 矩阵的标量乘法 λ*A=λ*每个元素,*A*B=A*λ*B
- 行列式的标量乘法,λ*|A|=λ*某1行/列
3.3.2 其他数乘对比
- 矩阵的标量乘法 (λ*A)=λ*(A)和标准的数乘无差别
- 行列式的标量乘法,|λ*A|=λ^n*|A| ,其中n是满秩矩阵A的秩/维度
- 原因是,每行的λ 都可以提出来,因此是n 个λ 相乘=λ^n
3.4 乘法
- 矩阵乘法
- 矩阵乘法:点乘
- 矩阵乘法:叉乘
- 行列数乘法: |Ann*Bnn| =|Ann|*|Bnn|
- 行列数乘法: |2Ann*Bnn| =|2Ann|*|Bnn| =2^n*|Ann|*|Bnn|
4 初等线性变换的不同
线性变换包含,行的线性变换和列的线性变换
行的线性变换
- 行之间,交换
- 某行乘以倍数
- 某行乘倍数+到其他行
列的线性变换
- 列之间,交换
- 某列乘以倍数
- 某列乘倍数+到其他列
4.1 对矩阵进行线性变换
- 无论是线性行变换,还是线性列变换,矩阵的不变
-
矩阵进行线性变换后的结果
- 线性变换前后系统的特征值不变;
- 线性变换前后系统的传递函数矩阵不变;
4.2 对行列式进行线性变换呢?
- 交换:如果交换行列式|A| 的任意两行/列,增加一个负号-
- 倍数:如果行列式|A| 某1行或列*λ,|A| 变成 λ*|A|
- 倍加:如果行列式|A| 某1行或列*λ后,再加到另外某1行/列,|A| 不变还是=|A|
- 总结,只有进行倍加的线性变换之后,行列式才不变化
解释原因
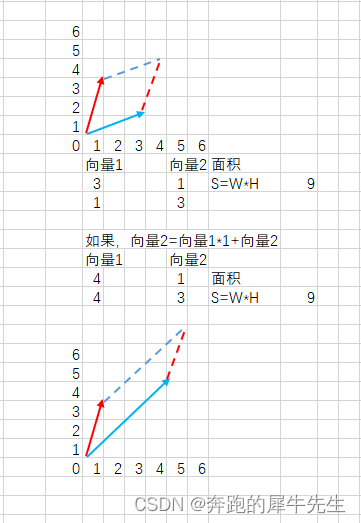
- 因为行列式其实代表有向的面积比,所以交换行列式|A| 的任意两行/列,增加一个负号-
- 因为行列式的标量乘法 λ*|A|= 把行列式的某1行/列* λ,所以行列式|A| 某1行或列*λ,|A| 变成 λ*|A|
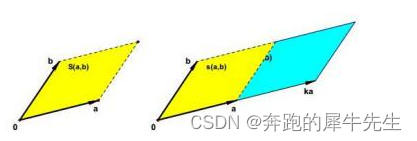
- 因为行列式其实代表有向的面积比,所以行列式|A| 某1行或列*λ后,再加到另外某1行/列,|A| 不变还是=|A|




![[JavaWeb]【十三】web后端开发-原理篇](https://img-blog.csdnimg.cn/344a1e69a0264e5d9413a3466436acda.png)