Codeforces Round 887 Div.3 A~D

文章目录

- A. Blackboard List
- B. Minimize Permutation Subarrays
- C. No Prime Differences
- D. Bracket Walk

A. Blackboard List

Problem - A - Codeforces

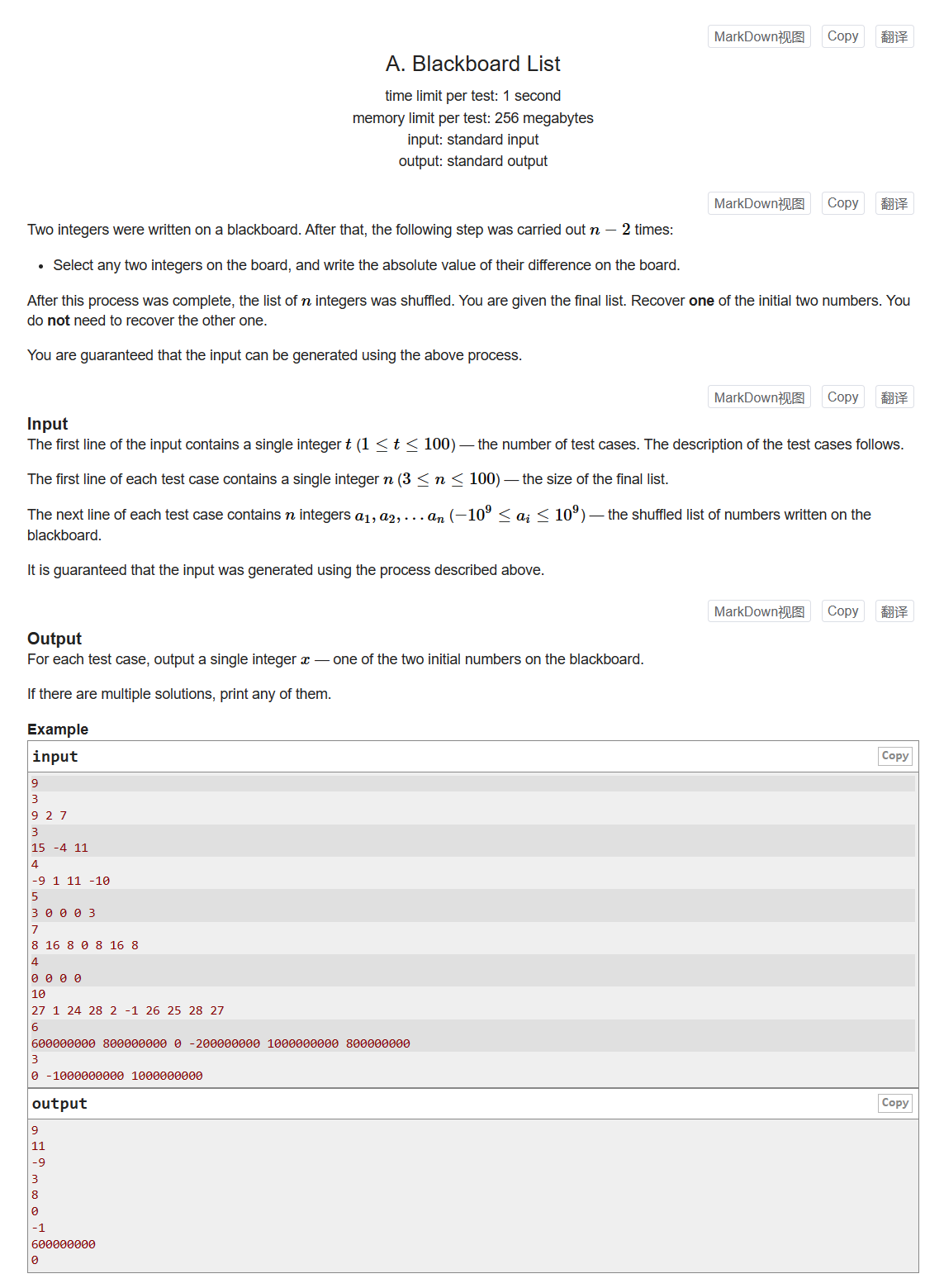
一个只有两个数的数组，选择数组中的任意两个数，计算它们差值的绝对值并加入数组
给定一个长度为n的数组，该数组经过了n-2次以上操作，问原数组中的数？（输出两个中的任意一个）

由于加入数组的数都是正数，所以数组中的负数一定是原数
若数组中的数都是正数，由于每次计算的都是两者之间差值的绝对值，该值一定小于两数中较大的数。所以数组中最大的数一定是原数

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;
int T, n, a[N];

int main()
{
    cin >> T;
    while ( T -- )
    {
        cin >> n;
        for (int i = 0; i < n; ++ i ) cin >> a[i];
        int mn = *min_element(a, a + n);
        int mx = *max_element(a, a + n);
        if (mn < 0) cout << mn << endl;
        else cout << mx << endl;
    }
    return 0;
}

B. Minimize Permutation Subarrays

Problem - B - Codeforces

对于长度为n的数组，若数组中的数分别是1~n中的所有数，那么该数组为n的全排列
给定长度为n的全排列，交换数组中的两个数，使得数组的子数组中，全排列数量最小

根据全排列的性质，1. 数组中的数不能重复，由于原数组本身就是全排列，所以其子数组中不会出现重复的数，故无法往这个方向构造。2. 长度为n的数组中不可能出现大于等于n+1的数，根据这个性质，我们可以构造一种情况，使得子数组出现n或者大于子数组长度的数
继续考虑，长度大于2的全排列中，一定会出现1与2。由于子数组必须是连续的这个性质，原数组1到2之间的所有数必须被包含

比如：1 3 2 5 4，前三个数构成的子数组1 3 2是一个全排列，其长度大于2，那么一定会包含原数组中1到2之间的数。而1到2之间的数为3，是一个小于等于数组长度的数，若1到2之间的数为一个大于数组长度的数，比如1 4 2 5 3或者1 5 2 3 4，前三个数构成的子数组不再是全排列

所以，无论如何选取子数组，子数组中一定有两个子数组是全排列，它们的长度为1和n。剩下的子数组，我们需要构造一种情况，使得原数组的1到2之间存在大于子数组长度的数。要使所有子数组的全排列数量最小，将n放入1到2之间，此时原数组的所有子数组中只存在两个全排列

因此，这道题的做法是：找出1，2和n的位置，若n不在1和2之间，将n与1（或2）交换
将 $a [i]$ 作为p数组的下标，用p数组存储 $a [i]$ 在a数组中的下标，即 $p [a [i]] = i$
最后将1，2，n三者的下标进行排序，输出n的下标与中间的下标

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 2e5 + 10;
int T, a[N], p[N], n;

int main()
{
    cin >> T;
    while ( T -- )
    {
        cin >> n;
        int i1, i2, in;
        for (int i = 1; i <= n; ++ i ) 
        {
            cin >> a[i];
            p[a[i]] = i;
        }
        
        int b[] = { p[1], p[2], p[n] };
        sort(b, b + 3);
        cout << b[1] << ' ' << p[n] << endl;
    }
    return 0;
}

参考了灵神的思路与代码，对比自己的代码后，不得不说，灵神的代码是真的简洁

C. No Prime Differences

Problem - C - Codeforces

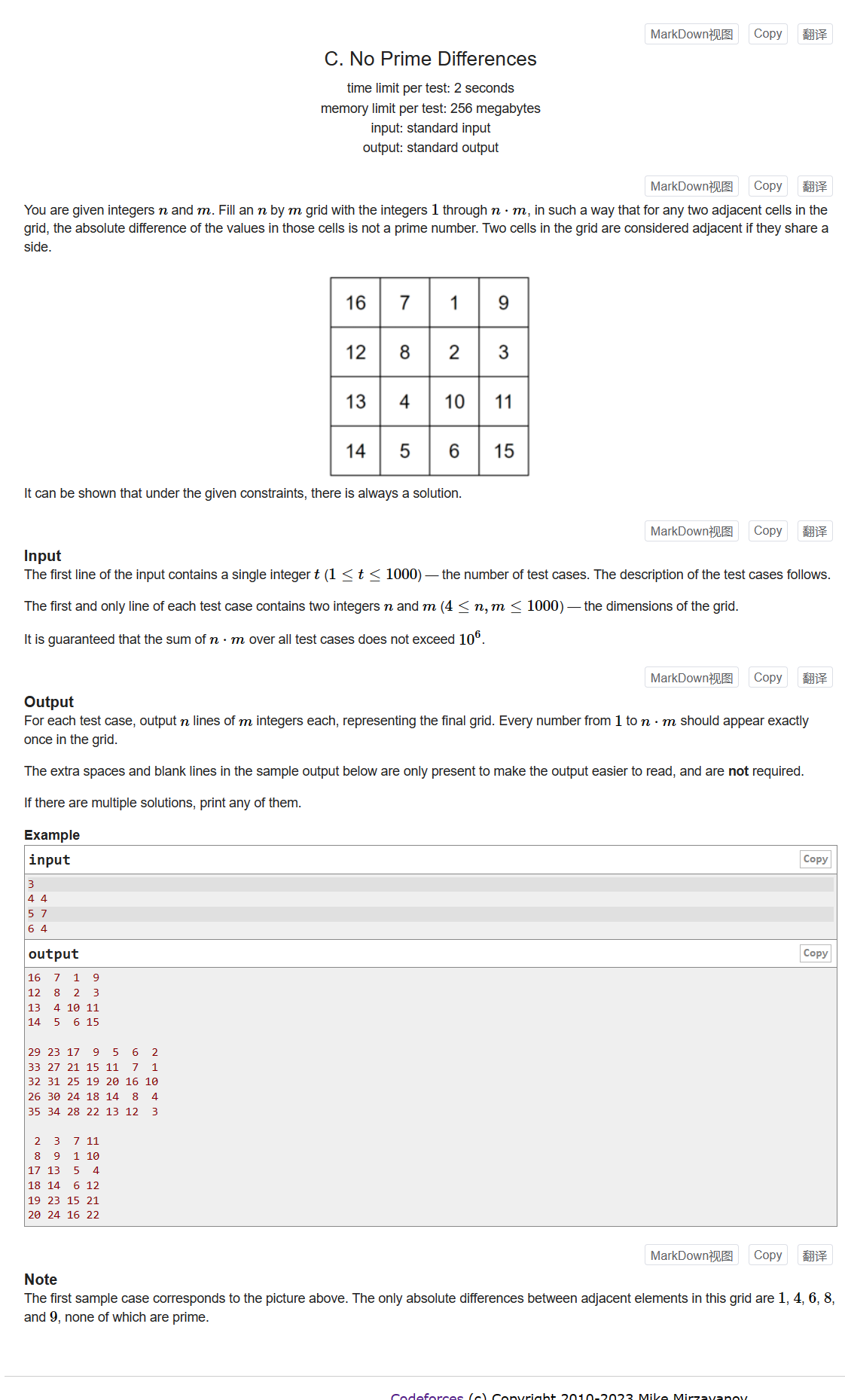
给定矩阵的n和m，矩阵中的数为1~ $n * m$ ，构造一个矩阵，使得（上下左右）相邻的数，绝对值为非质数
矩阵的构造一般有几种：1. 横着构造 2. 竖着构造 3. 斜着构造 4. 染色构造（每次构造不相邻的格子）
这题可以横着构造，若n为4，m为4，先构造第一行1 2 3 4，这样一行中的每个数相差1，满足题意
再构造剩余行：
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
每一列中，相邻元素相差4，满足题意。若交换每一行的位置，矩阵依然满足题意，因为每一列相邻元素的差值为m的倍数，m为非质数，其倍数一定是非质数。若m为质数，其两倍以上的数才是非质数
若n为4，m为5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
每一行中的相邻元素相差1，满足题意，每一列的相邻元素相差5，不满足题意。考虑行的交换
11 12 13 14 15
1 2 3 4 5
16 17 18 19 20
6 7 8 9 10
此时满足题意，若m和n都为5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
交换：
1 2 3 4 5
11 12 13 14 15
21 22 23 24 25
6 7 8 9 10
16 17 18 19 20
可以发现，当m为质数时，要使每一列的相邻元素相差非质数，这个差值必须是m的两倍或者两倍以上
也就是将：奇数行变成相邻行，偶数行变成相邻行，使得矩阵的上一半为原来的奇数行，下一半为原来的偶数行
此时矩阵的两部分都满足题意，但是上半部分和下半部分的相邻行，如果本来就是相邻行呢？如：
1 2 3 4 5
11 12 13 14 15
6 7 8 9 10
16 17 18 19 20
11所在行与6所在行本来就是相邻行，此时矩阵中只有这两行不满足题意。将奇数行的第一行1与偶数行的最后一行16作为相邻行，那么一定满足题意
6 7 8 9 10
16 17 18 19 20
1 2 3 4 5
11 12 13 14 15
即，交换上下两个部分，偶数行在上，奇数行在下

综上，这题的构造方式是：

从左往右，从上往下，将1~n*m填入格子，此时行中的相邻元素满足题意，考虑列的构造
将偶数行作为矩阵的上半部分，奇数行作为矩阵的下半部分

#include <iostream>
using namespace std;

const int N = 1010;
int a[N][N];
int T, n, m;

int main()
{
    cin >> T;
    while ( T -- )
    {
        cin >> n >> m;
        for (int i = 1, x = 1; i <= n; ++ i )
            for (int j = 1; j <= m; ++ j )
                a[i][j] = x ++ ;
        
        for (int i = 2; i <= n; i += 2)
        {
            for (int j = 1; j <= m; ++ j )
                cout << a[i][j] << ' ';
            cout << endl;
        }
        for (int i = 1; i <= n; i += 2)
        {
            for (int j = 1; j <= m; ++ j )
                cout << a[i][j] << ' ';
            cout << endl;
        }
    }
    return 0;
}

D. Bracket Walk

Problem - D - Codeforces

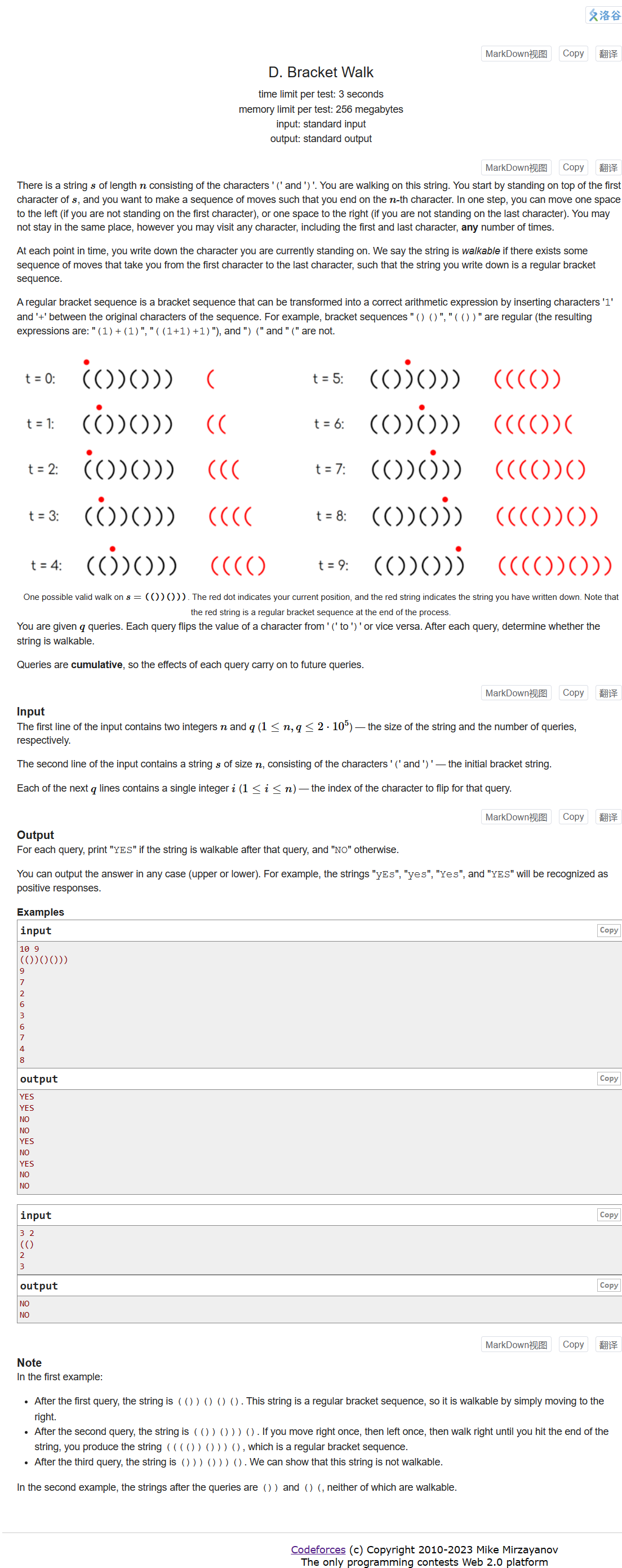
给定一个之包含1和-1的序列，从左到右走完这个序列，在不越界的情况下，每一步可以向左或向右走。将走过位置的数值累加，即 $s u m + = a [i]$ ，满足sum始终大于等于0，并且最后为0

问：将某个位置的数改为相反数后，是否满足题意？
判断YES或NO的题，先考虑NO的情况
若数组长度为奇数，那么sum最后的值一定不为0，输出NO

由于这题能往回走，考虑出现连续的1或者-1时，往回走1次对sum的影响
若出现k个连续的1，往回走1次，sum += (k - 2) * 2 + 2
若出现k个连续的-1，往回走1次，sum += (k - 2) * -2 + -2
所以只要k大于等于2，不论往回走几次，对sum的影响为一个偶数的变化，且最少变化2或-2

只要出现了连续的1，那么sum就能达到正无穷，只要连续的1之后存在连续的-1，那么sum就能回到0。所以连续1和连续-1之间的情况不需要考虑，因为无论情况怎样，最后都一定是0。所以只要保证连续1之前与连续-1之后，序列由( )组成。若出现( ))或者(( )，则视为不合法

那如何用代码实现呢？实现方式很巧妙，之前自己写了三份不同的，一大堆ifelse条件判断，依然是漏了一些情况。心态崩了，只好借鉴灵神的思路
假设用字符串保存括号序列，从0下标开始。规定偶数下标必须保存(，奇数下标必须保存)，即序列()()()()...。若真实序列的偶数下标保存)，那么记录该下标，同理，真实序列的奇数下标保存(，也记录该下标
所以，被记录的下标中，偶数下标为)，奇数下标为(。若最小值为奇数下标，并且最大值为偶数下标，说明真实序列中先出现((最后出现))，此时序列合法
若最小值与最大值都为偶数下标，说明真实序列中，第一次出现的连续括号与最后一次出现的连续括号都是))，显然不合法
若最小值与最大值都为奇数下标，说明真实序列中，第一次出现的连续括号与最后一次出现的连续括号都是))，也同样不合法

由于被记录的下标中，要取出最大与最小值，并且每次的询问操作还是叠加的，这里用set保存被记录的下标，begin()和人begin()返回的就是最小与最大值。每次判断要反转的括号是否在set中，若不在，则说明该下标上的括号原本是正确的，反转后将该下标加入set，若存在，将该下标从set中删除

#include <iostream>
#include <set>
using namespace std;

const int N = 2e5 + 10;
char str[N];
int n, q;
set<int> s;

int main()
{
    cin >> n >> q >> str;
    char a[3] = "()";
    for (int i = 0; i < n; ++ i )
        if (str[i] != a[i & 1])
            s.insert(i);

    while ( q -- )
    {
        int x;
        cin >> x;
        if (s.count(-- x)) s.erase(x);
        else s.insert(x);
        
        if (n & 1) cout << "NO" << endl;
        // 最小的是右括号（偶数），最大的是左括号（奇数）
        else if (s.size() && ((*s.begin() % 2 == 0) || (*s.rbegin() % 2))) cout << "NO" << endl;
        else cout << "YES" << endl;
    }
    return 0;
}