数据降维 | MATLAB实现T-SNE降维特征可视化

降维效果

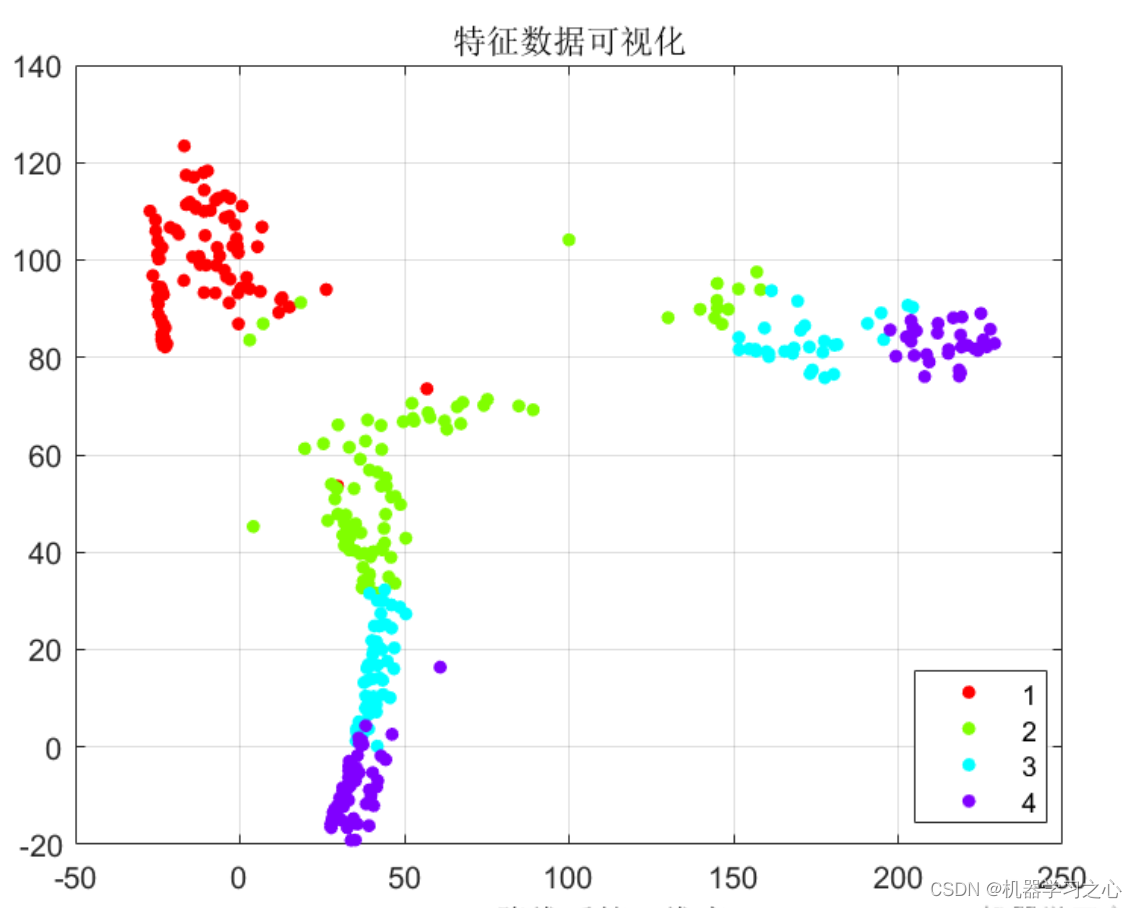
基本描述

T-SNE降维特征可视化，MATLAB程序。
T-分布随机邻域嵌入，主要用途是对高维数据进行降维并进行可视化，以便更好地理解和发现数据之间的结构、模式和聚类关系。它被广泛应用于数据可视化、数据挖掘和机器学习等领域。
包含二维图像和三维图像生成两部分；
EXCEL表格直接导入，更换Excel表格的数据即可。

程序设计

• 完整程序和数据获取方式：私信博主回复MATLAB实现T-SNE降维特征可视化。

%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
X1 = sum(p_train, 2);
tSb = tSb - X1 * X1' / num_s - tSw;

tSb = (tSb + tSb') / 2;
tSw = (tSw + tSw') / 2;

if r == num_d
  [eigvec, eigval_matrix] = eig(tSb, tSw);
else
  opts.disp = 0; 
  [eigvec, eigval_matrix] = eigs(tSb, tSw, r, 'la', opts);
end

eigval = diag(eigval_matrix);
[sort_eigval, sort_eigval_index] = sort(eigval);
T0 = eigvec(:, sort_eigval_index(end: -1: 1));
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% 确定嵌入空间中的度量
switch metric
  % 加权特征向量
  case 'weighted'
   T = T0 .* repmat(sqrt(sort_eigval(end: -1: 1))', [num_d, 1]);
  % 正交归一化
  case 'orthonormalized'
   [T, ~] = qr(T0, 0);
  % 原始特征向量
  case 'plain'
   T = T0;
end
————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/130454138

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229