Python解题 - CSDN周赛第15期

本期遇上官方大放水，四道题里有三道都在每日一练里做过，再加上比赛时间不太友好，参与人数不多，问哥竟然混了个第一名，真是惭愧。。。就当是官方在奖励那些平时多多参加每日一练的童鞋们了。

第一题：求并集

由小到大输出两个单向有序链表的并集如链表 A {1 -> 2 -> 5 -> 7} 链表 B {3 -> 5 -> 7 -> 8} 输出: {1 -> 2 -> 3 - > 5 -> 7 -> 8} 。

示例1
输入
4 4

1 2 5 7

3 5 7 8

输出 1 -> 2 -> 3 - > 5 -> 7 -> 8

分析

大水题，真没啥好分析的，就是两个列表合并排序，去重。使用python的列表合并、转集合去重、再转列表排序输出，就pass了。

要吐槽的是最后的输出格式，给的示例是要在每个数字之间添加“ -> ”的符号，结果自测默认的结果里“->”左右却没有空格，所以使用自测对比的童鞋估计会怀疑很久。。。

参考代码1

list_a = list(map(int, input().split()))
list_b = list(map(int, input().split()))
print(" -> ".join(map(str, sorted(set(list_a + list_b)))))

当然，可以看到上面代码虽然简单，但对列表的遍历了好几遍。因为python力图将一些基本功能放进黑盒子（内置函数），使代码整体变得优雅，但牺牲了一些效率（虽然对本题没有影响）。如果想深入思考更进一步，本题可以借鉴归并排序的思路，对两个列表排序后依次加入新的列表：

参考代码2

list_a = list(map(int, input().split()))
list_b = list(map(int, input().split()))
list_a.sort() # 默认给的是排好序的列表，所以其实不用排序，只是注明要对升序列表进行此操作
list_b.sort() # 同上
i = j = 0
res = []
while i<len(list_a) and j<len(list_b):
    if list_a[i] < list_b[j]:
        res.append(list_a[i])
        i += 1
    elif list_a[i] > list_b[j]:
        res.append(list_b[j])
        j += 1
    else:
        res.append(list_a[i])
        i += 1
        j += 1
res.extend(list_a[i:])
res.extend(list_b[j:])
print(" -> ".join(map(str, res)))

第二题：小T找糖豆

已知连续序列A，包含1e18个元素，分别是[1,1e18]。现在去除序列中的n个元素. 得到新的连续序列[X,1e18]，该序列中最小元素是？

示例1 示例2
输入
3

1 2 3

4

3 5 6 8

输出 4 9

分析

超级大水题。一开始问哥还在纳闷题目什么意思，结果是脑筋急转弯，谜底就在谜面上。。。

题目所谓的[1, 1e18]的大数组不可能真的用内存开出来，所以我们只要找到给出的几个数字里最大的数字，这个数字右边相邻（加一）的数字，就是新的分割后的[x, 1e18]数组里最小的数字。因为新的数组里的数字也要连续，所以分割的左边以及中间那些部分就全都舍弃了。（比如示例2里，4个数字可以分成[1, 2]，[4]，[7]，[9, 1e18]，只取[9, 1e18]作为新的序列）

代码就一句话的事。。。

参考代码

n = int(input())
arr = list(map(int, input().split())
print(max(arr) + 1)

第三题：争风吃醋的豚鼠

N个节点两两建边。不存在3个节点相互之间全部相连（3个节点连接成环）。最多能建立多少条边？

示例

示例1 示例2
输入
4

5

输出 4 6

分析

本题就在不久前在每日一练中遇到过，也有点脑筋急转弯的意思。题目描述有点绕，但其实就是问n个节点如果不准连成三角形的话可以连出多少条边。

如下图就可以简单列出当节点个数分别是2到5的时候，可以连出哪些合法边。注意图中黄色点状线表示无法成立的边，因为会使某三个点构成一个三角形：

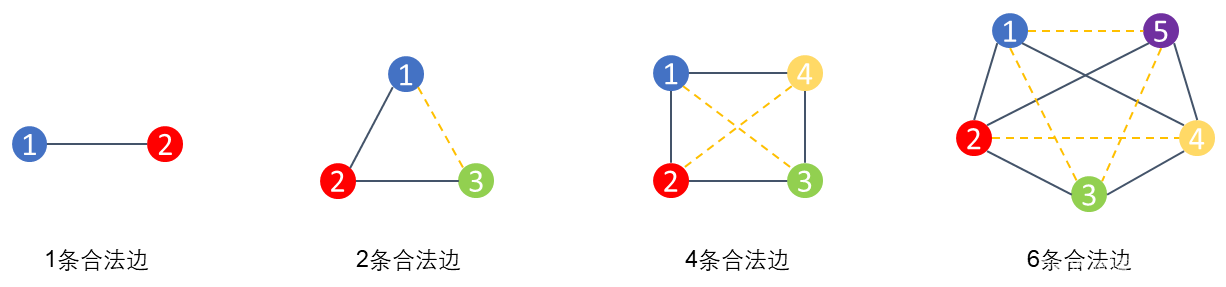
大家都知道，给出n个节点，如果没有任何限制的话，相互连接组成full mesh，可以有 $n(n-1)/2$ 条边，表示每个节点（n）都和除了自己以外的其他所有节点（n-1）构成一条边。按照这个思路，我们可以模拟每个节点和其他节点组边的过程。如果把上图最右边5个节点的图摊平来看：

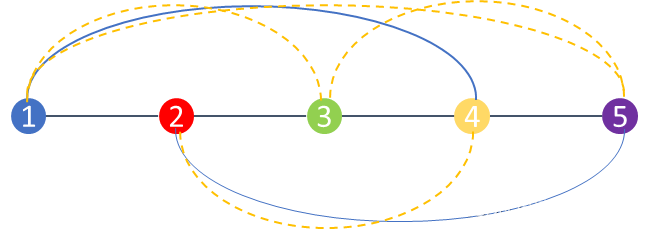
很明显可以发现，为了避免形成三角形，每个节点，向其他节点组边的时候，除了相邻的节点（上图中水平的边），其他节点都需要跳过一个节点才能组边。

节点1：和节点2组边、跳过节点3、和节点4组边、跳过节点5
节点2：和节点3组边、跳过节点4、和节点5组边
节点3：和节点4组边、跳过节点5
节点4：和节点5组边

那么，如果我们增加节点数会看到什么呢？比如有9个节点摊平互连，按照上述规律对每个节点向其右边的节点组边的话，我们就得到了下面这张图。

节点1右边与其能够构成合法边的节点为：2、4、6、8
节点2右边与其能够构成合法边的节点为：3、5、7、9
节点3右边与其能够构成合法边的节点为：4、6、8
节点4右边与其能够构成合法边的节点为：5、7、9
节点5右边与其能够构成合法边的节点为：6、8
节点6右边与其能够构成合法边的节点为：7、9
节点7右边与其能够构成合法边的节点为：8
节点8右边与其能够构成合法边的节点为：9

发现规律了没？从左到右遍历每个节点，每个节点和其右边节点所能构成的边的数量就等于其右边节点数量的一半（向上取整），然后将所有节点能够构成的合法边的数量累加即可。之所以向上取整，是因为当右边节点数量为奇数时，当前节点恰好和最右边的节点可以构成合法边（比如节点2和节点9）。

于是，我们的代码也就呼之欲出了：

参考代码

n = int(input())
result = 0
for i in range(1, n+1):
    result += (n-i)//2 + bool((n-i)%2) # 向上取整
print(result)

向上取整可以使用math模块里的ceiling()函数，但问哥习惯借助python语言里布尔值可以直接参与数学运算的特点，有余数则加一，没有则加零。

当然本题还可以继续深入，找出通用的数学公式，但原理大同小异，不再赘述。

第四题：选择客栈

丽江河边有 n 家很有特色的客栈，客栈按照其位置顺序从 1 到 n 编号。每家客栈都按照某一种色调进行装饰（总共 k 种，用整数 0 ~ k-1 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 p 。他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 p 元的咖啡店小聚。

第一行三个整数 n, k, p，用空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 n 行，每行两个整数，空格隔开，分别表示客栈的装饰色调和咖啡店的最低消费。

示例：

示例
输入
5 2 3

0 5

1 3

0 2

1 4

1 5

输出 3

分析

本题是洛谷原题，但问哥首次遇到这道题还是在CSDN的每日一练里。检查了一下参数都没有变化，就直接套上之前做此题的思路了。（问哥也推荐大家在做题的时候不要一上来就翻题解，先自己思考，结合以前学习到的知识，去试着找到思路，这样印象会更深。）

问哥之前做此题时，首先想到的也是暴力穷举。拿示例举例，5个客栈、2种色调、最高消费3，那这矫情的两人能喝得起咖啡的地方只有客栈2（最高消费3）和客栈3（最高消费2），于是就在这个位置穷举其左右两边（包括自己）有多少对相同色调的客栈。可以看到，符合要求的客栈分别是客栈1与客栈3、客栈2与客栈4、客栈2与客栈5，共三种可能的组合，答案就是3。

当然，数据量小的时候穷举完全可行，但是作为比赛的压轴题，不太可能靠穷举就能过关。于是，这样写代码的话一定会爆。而且由于问哥是在CSDN的每日一练里刷到此题，而每日一练还贴心地提示了本题属于动态规划的范畴，所以一定有更好的解法。

于是，为了找到规律，问哥还是老办法，将客栈的位置画在纸上：

我们来模拟这俩人选客栈的过程，假设他俩从左向右依次遇到客栈。

当遇到第一间客栈时，其咖啡馆的最低消费是5，高于他们的预算3，而且一个客栈也住不下他俩（矫情），但是也许后面可以住到，于是他们在小本本上记下遇到配色0的客栈1间，但是因为没有合适的咖啡馆，所以（暂）不可选，记为0，而题目要求找的可选的客栈自然也是0对（只有1间）。

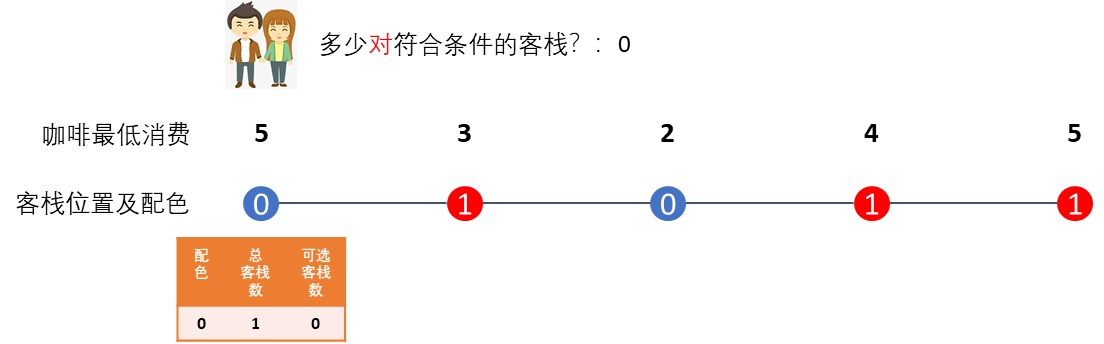
于是，他们继续向右走，遇到第二间客栈时，发现该客栈的咖啡馆最低消费3，刚好符合他们的要求，但是配色不一样，于是记下新发现了配色1的客栈1间，由于咖啡馆符合要求，所以配色1的客栈符合住的条件，而同样地，由于找到这间咖啡馆，使得之前遇到的配色0的客栈也符合住的条件了（重要），所以修改小本本的记录如下图中所示。代表的含义为：如果后面再遇到同样配色的客栈，那么对应配色可选的客栈数量都记在表里了。

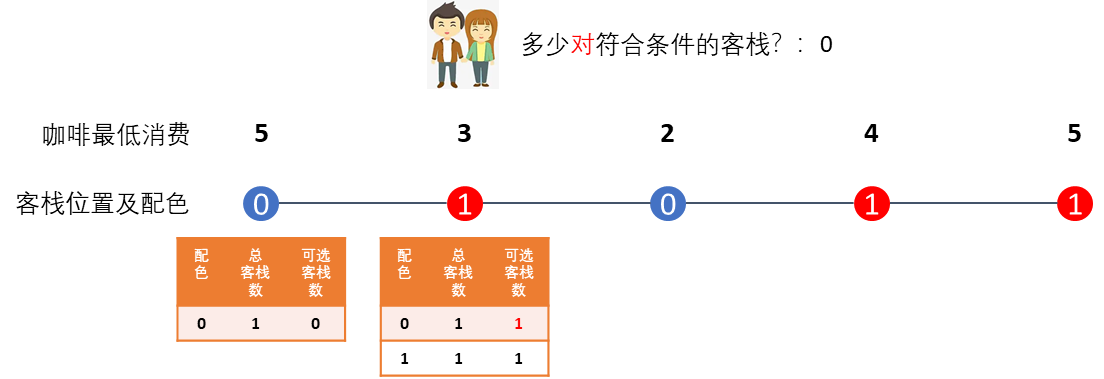
继续往右走，他们遇到第三间客栈，配色是0，于是，找到小本本中记录的同样配色0的可选客栈数为1，所以这一对客栈符合条件，答案更新为1。

然后，因为后面还有客栈，他们想知道总共有多少对，所以需要继续更新表格，于是配色0的客栈数更新为2，而可选客栈数呢？这时他们发现这家客栈的咖啡馆最高消费为2，低于他们的预算3，甚喜，很显然，这间客栈和右边还没遇到的客栈也可以配对，于是两间配色0的客栈都可选（都可以与右边客栈配对），数字更新为2。

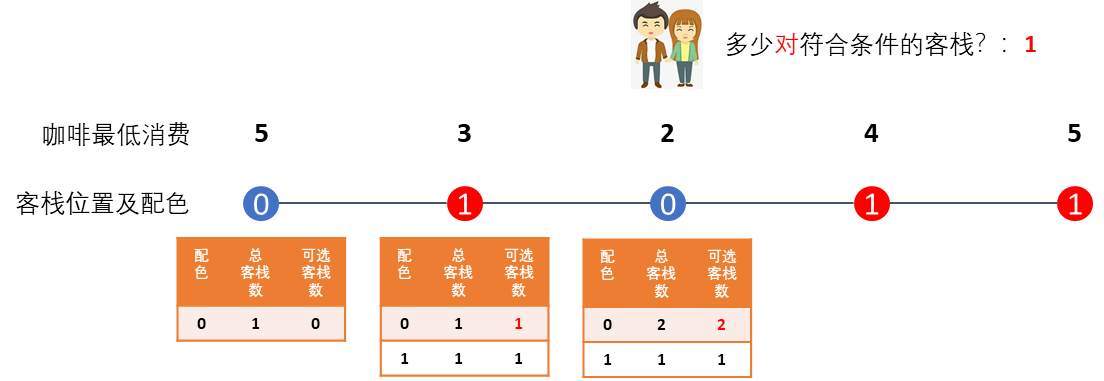
继续往右走，这二人遇到的第四间客栈配色为1，于是翻看小本本，发现表中记录了前面遇到过的配色1的客栈有一间是可选的，正好可以和现在这间配对，于是答案更新为2。

但是，由于该客栈的咖啡馆太贵了，超出他们的预算，使得这家客栈不能成为右边客栈的备选，所以可选的配色1的客栈数量还是没有变化。（意味着可以和右边的相同配色客栈配对的客栈数量没有变化）。

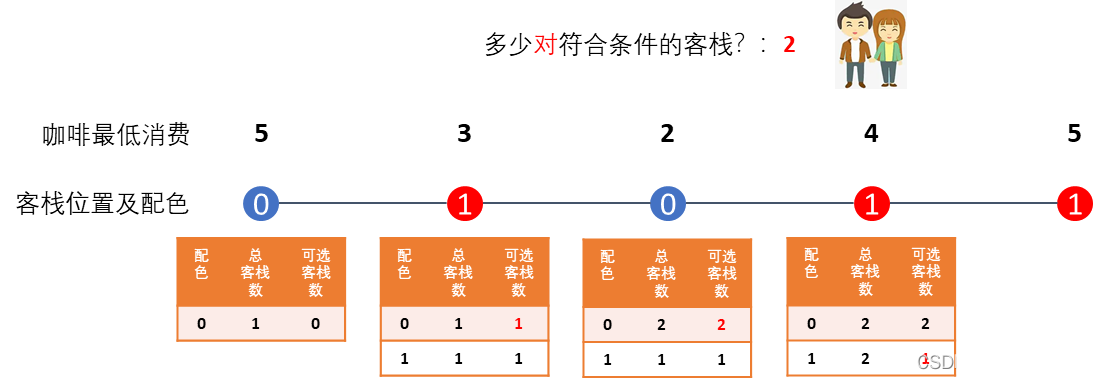
到了最后一间客栈，发现配色还是1，于是翻看小本本，发现配色1的可选客栈数量还是1，于是加上1就得到了最终的答案：3。因为是最后一间客栈，理论上他们不需要再更新小本本了，但是他们的强迫症（代码一致性）犯了，打听了咖啡馆的最低消费，发现并不符合条件，于是将表格更新如下图：

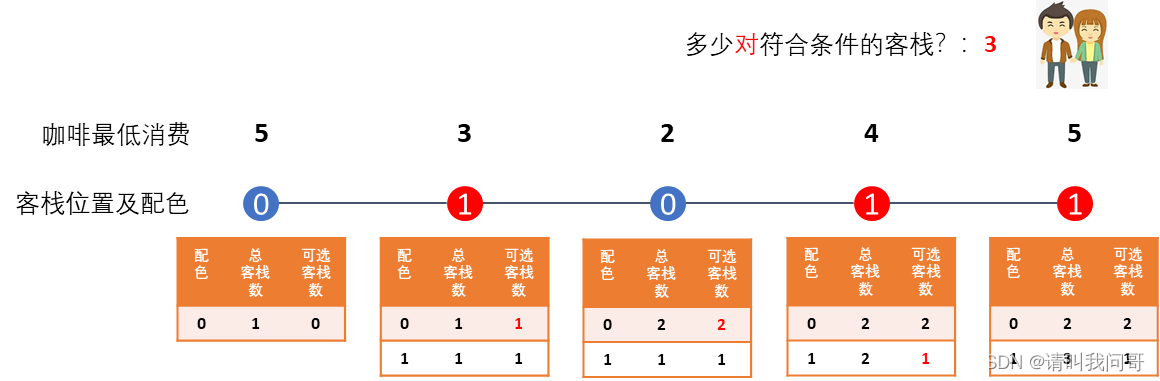
我们总结一下：

首先，我们建一张二维表，横纵坐标分别表示客栈的配色方案与该配色的总客栈数及可选客栈数。然后，我们从左向右遍历客栈列表。
遇到新的客栈，先查表，检查和当前客栈同样配色的客栈里有多少符合配对条件的客栈，加上答案。
再更新已经遇到的该配色方案的客栈总数（加上当前客栈）。
最后检查该客栈里咖啡馆的最低消费，如果高于预算，则不管。
如果该客栈咖啡馆的最低消费不高于预算，符合条件，则更新之前遇到的所有配色方案的客栈为可选。（修改可选客栈数等于总客栈数）
继续下一间客栈，重复上面步骤2到5，直到最后。

至此，本题就已经解出90%了。然而，上面例子里还漏掉了一种情况。那就是如果连着遇到好几个配色相同的客栈，却没有遇到符合条件的咖啡馆，直到遇到符合条件的咖啡馆后，所有之前的咖啡馆全变成可选了。在这种情况下，我们要更新的答案需要加上之前同配色的客栈总数，而不是可选客栈数。

比如，如果我们把第二间客栈咖啡馆的最低消费修改为5，高于预算3，那么这二人遇到第三间咖啡馆的时候，左边两间客栈都不可选，但是，由于第三间客栈的咖啡馆符合要求，于是所有遇到过的客栈都可以配对了，答案应该加上客栈总数1（也就是有1对客栈符合条件），然后，再根据上面描述的步骤更新表格。

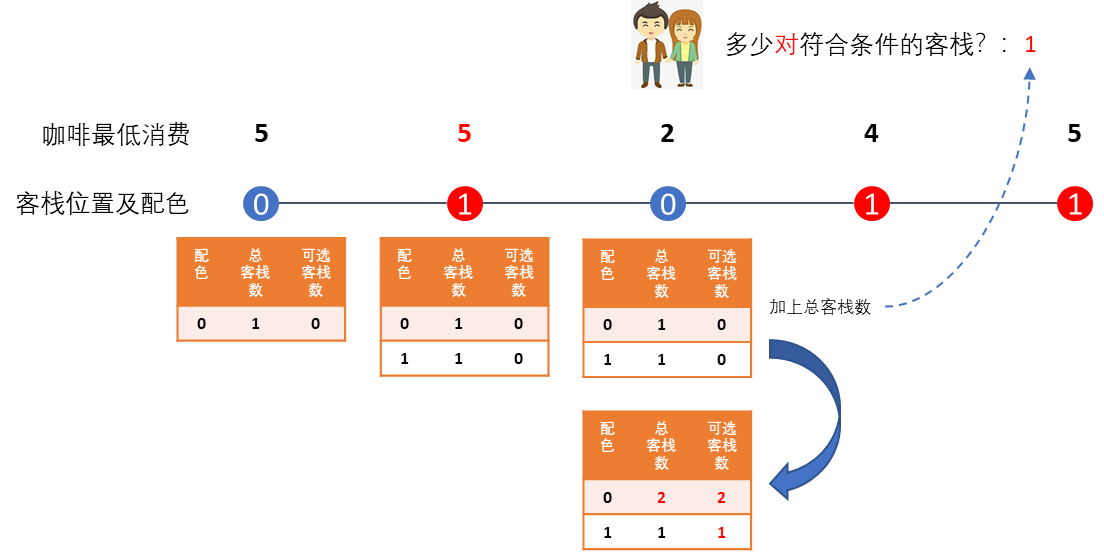
所以，我们在前面描述的步骤里加上这个条件的判断：

首先，我们建一张二维表，横纵坐标分别表示客栈的配色方案与该配色的总客栈数及可选客栈数。然后，我们从左向右遍历客栈列表。
遇到新的客栈，先检查该客栈咖啡馆的最低消费，再查表，如果最低消费高于预算，则把答案加上和当前客栈同样配色的可选客栈数量；如果不高于预算，则加上同样配色的客栈总数。
再更新已经遇到的该配色方案的客栈总数（加上当前客栈）。
最后再检查一遍该客栈里咖啡馆的最低消费，如果高于预算，则不管。
如果该客栈咖啡馆的最低消费不高于预算，符合条件，则更新之前遇到的所有配色方案的客栈为可选。（修改可选客栈数等于总客栈数）
继续下一间客栈，重复上面步骤2到5，直到最后。

根据这个思路写出的代码如下：

参考代码

n, k, p = map(int, input().strip().split())
inn = []
for i in range(n):
    inn.append(list(map(int, input().strip().split())))

res = 0
dp = [[0]*2 for _ in range(k)] # 步骤1
for i in range(n):
    res += dp[inn[i][0]][0] if inn[i][1] <= p else dp[inn[i][0]][1] # 步骤2
    dp[inn[i][0]][0] += 1 # 步骤3
    if inn[i][1] <= p: # 步骤4
        for j in range(k): # 步骤5
            dp[j][1] = dp[j][0]
print(res)