Problem L. Partially Free Meal

题面

官方题解

官方题解解读

w(k,x)计算部分

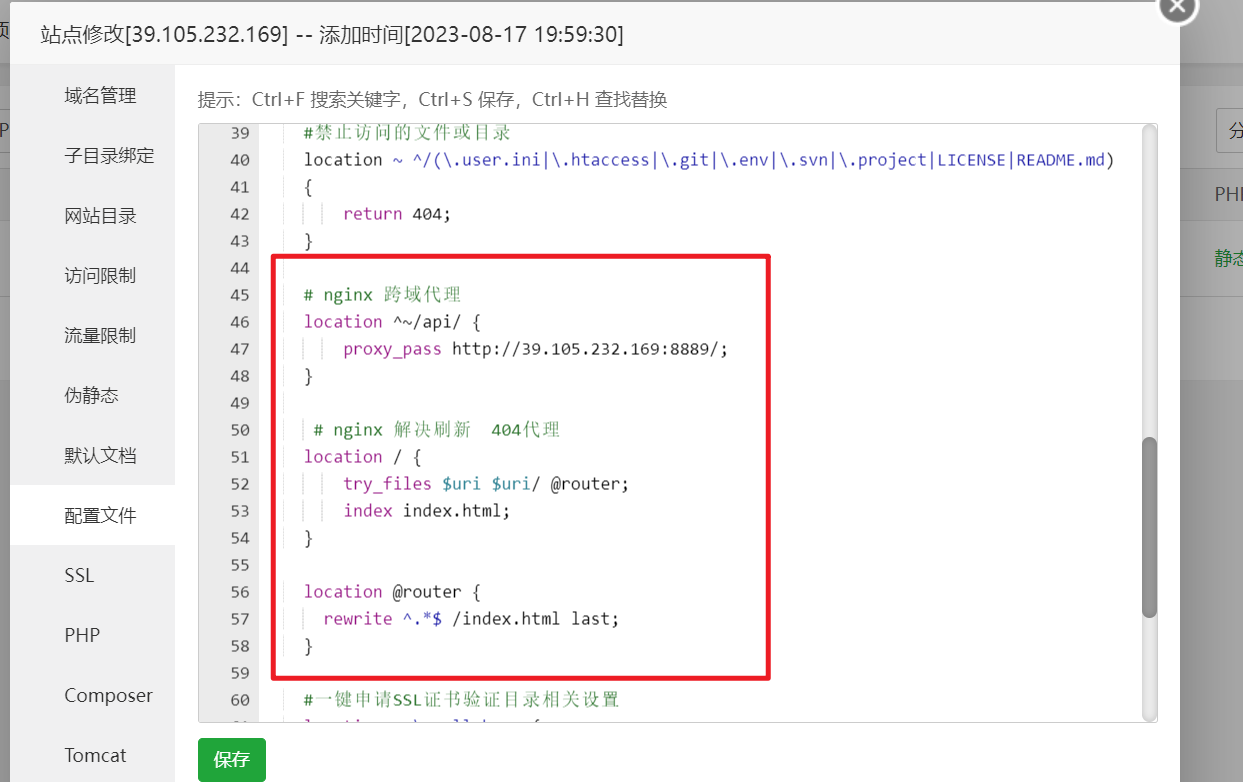
主席树常规做法，在一般主席树中多维护一个这个区间的总和就ok了

根据单调性分治求解部分

$接下来我们来推导一下单调性，也就是题解中的f(1)<=f(2)<=f(3)$
$比如我们f(1)=i,设j<i,那么w(2,i)一定小于等于w(2,j)$
$因为w(2,i)和w(2,j)就相当于在w(1,i),w(1,j)基础上再选一个，然而i>j$
$那么i可选的新的点的范围就涵盖j可选新的点范围了，所以w(2,i)不可能大于w(2,j)$
$比如设f(k1)=i,j<i那么w(k1+1,i)<=w(k1+1,j)$
$证明如下：w(k1+1,i)是ai+bi+i前面最小的k1个ai的值，w(k1+1,j)是aj+bj+j前面最小的k个ai$
$就是在此基础上再多选一个，然而i>j那么i的选择范围涵盖了j$
$并且w(k1,i)<w(k1,j)所以w(k1+1,i)<=w(k1+1,j)$
$有了f(1)<=f(2)<=f(3)的决策单调性结论$
$我们发现我们要求的k范围是1-n暴力做法是针对每个k都跑一遍所有的x$
$n方复杂度肯定不行，这时候我们发现决策单调性，也就是f(2)肯定在f(1)及它后面$
$这时候就可以根据f(n)进行分治，每次把k区间分两半，暴力计算出f(mi{d}_k)$
$然后mi{d}_k左边的区间影响决策的x范围也就是1到f(mi{d}_k)-1$
$mi{d}_k右边的区间影响决策的区间就是f(mi{d}_k)+1到n$
$这样一共分为log(n)层，每层计算区间和为n，复杂度为nlog(n)$

---

拟定std代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;

int root[N], idx, n;
LL ans[N];
struct PST{
	int lson, rson;
	int num; LL sum;
}tr[N<<5];

struct node{
	int a, b;
	bool operator <(node & tem){
		return b < tem.b;
	}
}res[N];

vector<int> diz;

void build(int &x, int l, int r)
{
	x = ++idx;
	if(l == r) return;
	int mid = (l+r) >> 1;
	build(tr[x].lson, l, mid);
	build(tr[x].rson, mid+1, r);
}

int find(int x)
{
	return lower_bound(diz.begin(), diz.end(), x) - diz.begin() + 1;
}

void insert(int &x, int y, int l, int r, int c)
{
	x = ++idx; tr[x] = tr[y]; tr[x].num ++; tr[x].sum += diz[c-1];
	if(l == r) return;
	int mid = (l+r) >> 1;
	if(c <= mid) insert(tr[x].lson, tr[y].lson, 1, mid, c);
	else insert(tr[x].rson, tr[y].rson, mid+1, r, c);
}

LL query(int x, int l, int r, int k)
{
	if(l == r) return 1ll*diz[l-1]*k;
	int mid = (l+r) >> 1;
	int cur = tr[tr[x].lson].num;
	if(cur <= k)
	{
		return tr[tr[x].lson].sum + query(tr[x].rson, mid+1, r, k-cur);
	}
	else return query(tr[x].lson, l, mid, k);
}

void solve(int kl, int kr, int xl, int xr)
{
	if(kl > kr) return ;
	int kmid = (kl+kr) >> 1; LL cur = 1e18; int xmid = 0;
	for(int i = max(xl, kmid); i <= xr; i ++)
	{
		if(1ll*res[i].b + res[i].a + query(root[i-1], 1, diz.size(), kmid-1) < cur)
		{
			cur = 1ll*res[i].b + res[i].a + query(root[i-1], 1, diz.size(), kmid-1); xmid = i;
		}
	}
	ans[kmid] = cur;
	solve(kl, kmid-1, xl, xmid); solve(kmid+1, kr, xmid, xr);
}

int main()
{
	ios::sync_with_stdio(false); cin.tie(0);
	cin >> n;
	for(int i = 1; i <= n; i ++){
		cin >> res[i].a >> res[i].b;
		diz.push_back(res[i].a);
	} 
	sort(res+1, res+1+n);
	sort(diz.begin(), diz.end());
	diz.erase(unique(diz.begin(), diz.end()), diz.end());
	build(root[0], 1, diz.size());
	for(int i = 1; i <= n; i ++)
	{
		insert(root[i], root[i-1], 1, diz.size(), find(res[i].a));
	}
	solve(1, n, 1, n);
	for(int i = 1; i <= n; i ++)
	{
		cout << ans[i] << endl;
	}
	return 0;
}