题目

标题和出处

标题：二叉树的层序遍历 II

出处：107. 二叉树的层序遍历 II

难度

4 级

题目描述

要求

给你二叉树的根结点 $\text{root}$，返回其结点值自底向上的层序遍历（即从左到右，按从叶结点所在层到根结点所在层逐层遍历）。

示例

示例 1：

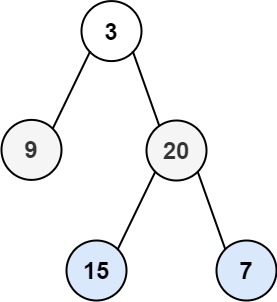
输入：$\text{root = [3,9,20,null,null,15,7]}$
输出：$\text{[[15,7],[9,20],[3]]}$

示例 2：

输入：$\text{root = [1]}$
输出：$\text{[[1]]}$

示例 3：

输入：$\text{root = []}$
输出：$\text{[]}$

数据范围

• 树中结点数目在范围 $\text{[0, 2000]}$ 内
• $\text{-1000}\le \text{Node.val}\le \text{1000}$

解法

思路和算法

这道题和「二叉树的层序遍历」相似，区别在于这道题要求按自底向上的顺序返回层序遍历的结果。

从根结点开始依次遍历每一层的结点，对于每一层维护一个结点值序列。由于这道题要求按自底向上的顺序返回层序遍历的结果，因此遍历完每一层结点之后，将该层结点值序列添加到层序遍历序列的头部。

为了在 $O(1)$ 时间内完成将一层结点值序列添加到层序遍历序列的头部，层序遍历序列应使用链表，在链表头部添加元素的时间是 $O(1)$。

代码

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> levelOrderTraversal = new LinkedList<List<Integer>>();
        if (root == null) {
            return levelOrderTraversal;
        }
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> levelValues = new ArrayList<Integer>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                levelValues.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            levelOrderTraversal.add(0, levelValues);
        }
        return levelOrderTraversal;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。每个结点都被访问一次，层序遍历序列使用链表时，每次将一层结点值序列添加到层序遍历序列的头部的时间是 $O(1)$，因此总时间复杂度是 $O(n)$。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是队列空间，队列内元素个数不超过 $n$。