目录
- 背包问题的简介
- 背包问题的定义
- 背包问题的分类
- 01背包问题
- 典型例题
- 实现思路
- 二维数组代码实现
- 一维数组优化实现
- 扩展:记忆化搜索 + DPS 实现
- 01背包之恰好装满
- 思路
- 代码实现
- 完全背包问题
- 典型例题
- 思路分析
- 二维数组代码实现
- 一维数组优化实现
- 多重背包问题
- 多重背包问题的三种解法
- 朴素解法
- 典型题目
- 思路
- 二维数组代码实现
- 一维数组优化实现
- 二进制解法
- 典型题目
- 思路
- 二维数组代码实现
- 一维数组优化实现
- 分组背包问题
- 典型例题
- 思路分析
- 二维数组代码实现
- 一维数组优化实现
背包问题的简介
背包问题的定义
一个可承载重量为 W W W 的背包和 N N N 件物品,每件物品有一个重量 w w w 和一个价值 v v v。现在让你用这个背包装物品,要求装入的物品总重量不能超过背包可承载重量 W W W,同时使装入物品的总价值最大。
背包问题的分类
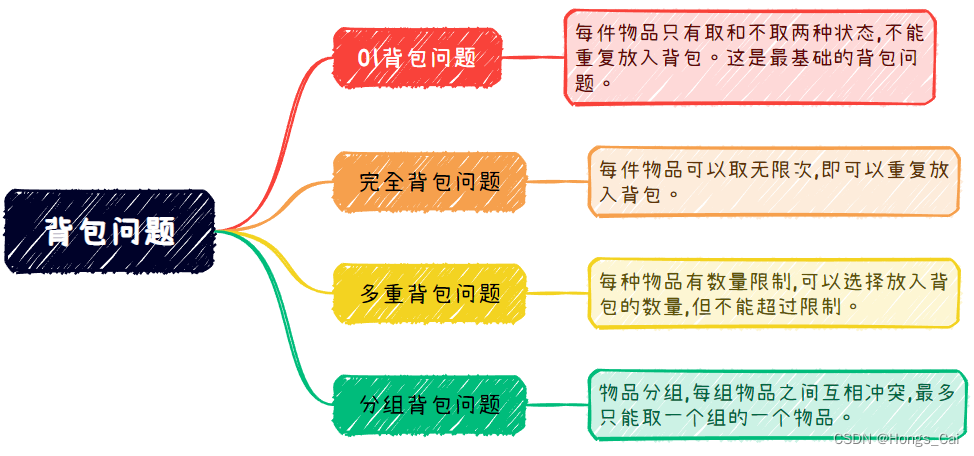
01背包问题
典型例题
题目描述:
有
V
V
V 件物品和一个容量是
V
V
V 的背包。每件物品只能使用一次。
第 i i i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i,w_i vi,wi,用空格隔开,分别表示第 i i i 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0
<
N
,
V
≤
1000
0 < N,V \leq 1000
0<N,V≤1000
0
<
v
i
,
w
i
≤
1000
0 < v_i,w_i \leq 1000
0<vi,wi≤1000
输入样例:
4 5
1 2
2 4
3 4
4 5
输出样例:
8
实现思路
DP问题的思路模板

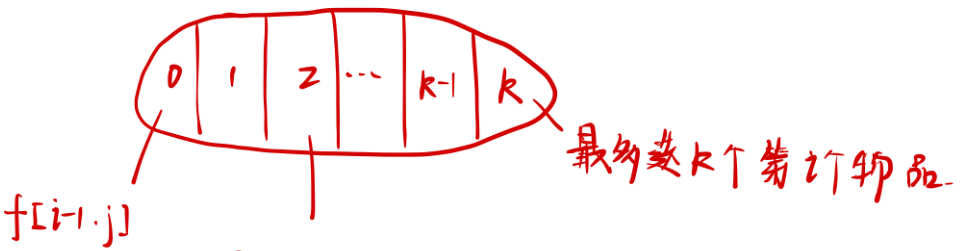
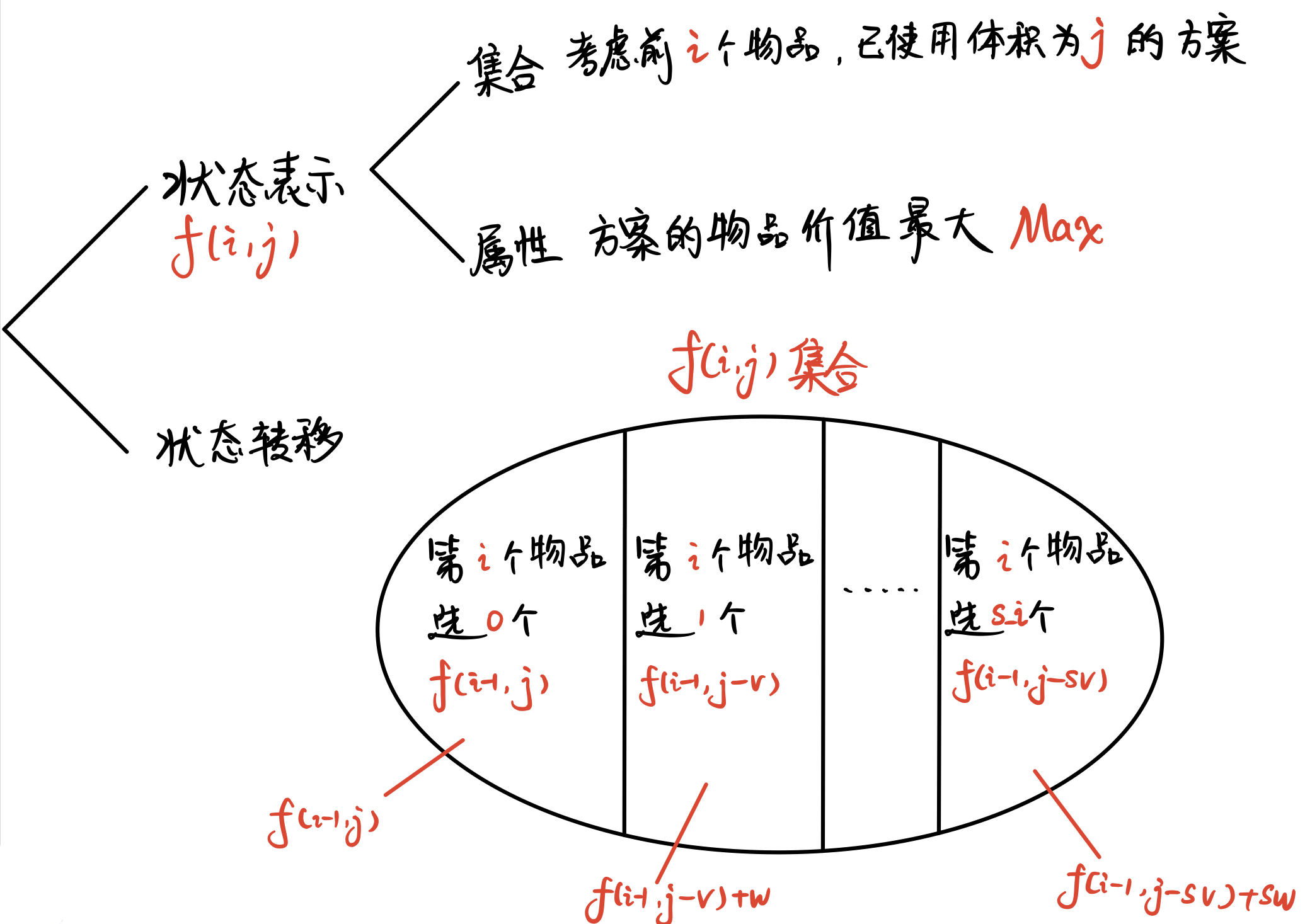
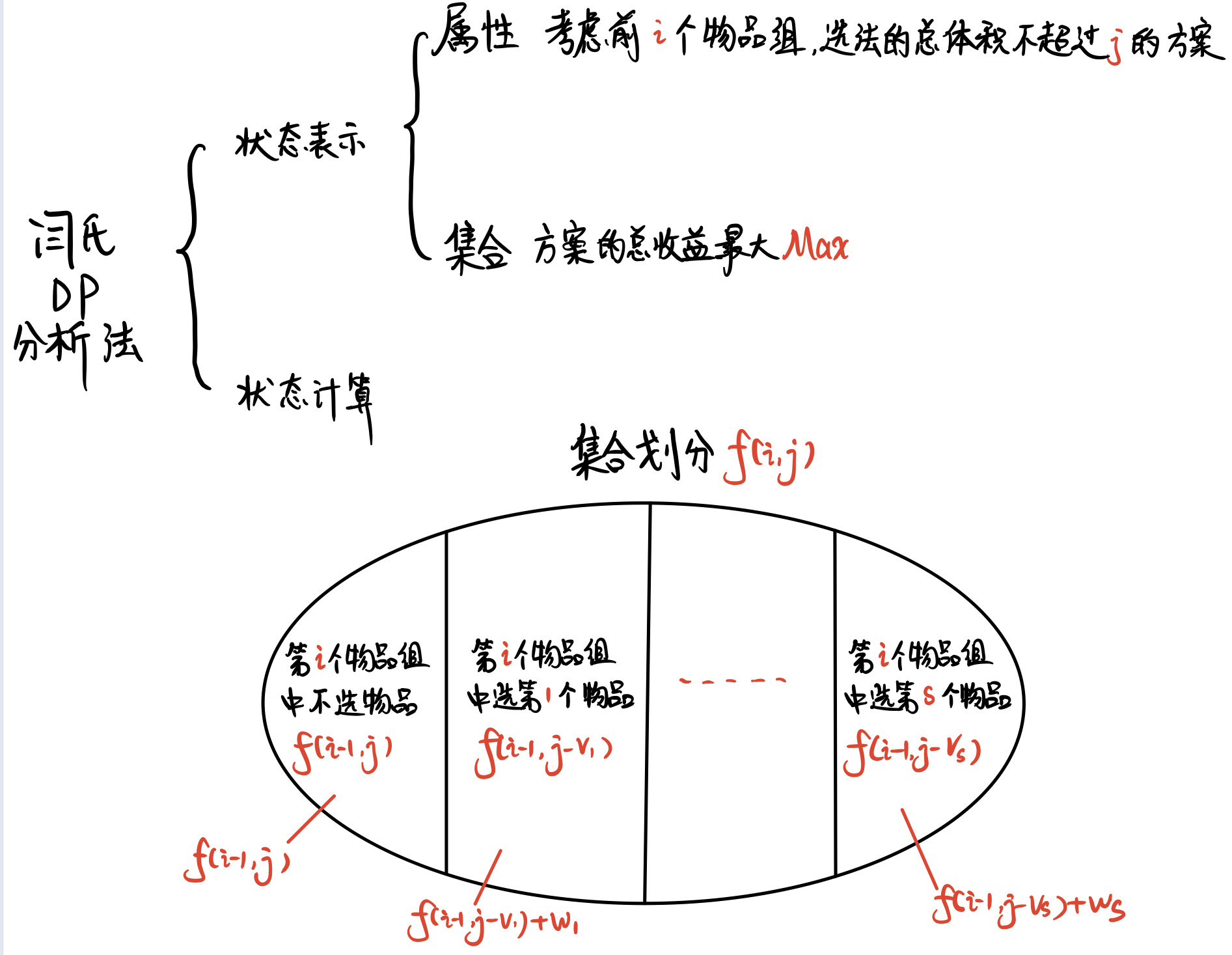
这里使用二维的状态表示 f [ i ] [ j ] f[i][j] f[i][j],用来表示 只从前 i i i 件物品中选, 总体积 ≤ j \leq j ≤j。
这样在状态计算中, 就可以把集合划分为 f [ i − 1 ] [ j ] f[i - 1][j] f[i−1][j](即只从前 i − 1 i - 1 i−1 件物品中选且不选择第 i i i 件物品), f [ i − 1 ] [ j − v [ i ] ] + w [ i ] f[i - 1][j - v[i]] + w[i] f[i−1][j−v[i]]+w[i]( v [ i ] v[i] v[i] 表示第 i i i 件物品的体积, w [ i ] w[i] w[i] 表示第 i i i 件物品的权重)(即只从前 i − 1 i - 1 i−1 件物品中选且选了第 i i i 件物品)。
通过以上思路可以得到状态转移方程:
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
−
1
]
[
j
−
v
[
i
]
]
+
w
[
i
]
)
\large f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i])
f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i])
二维数组代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int v[N], w[N], f[N][N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> v[i] >> w[i];
for (int j = 0; j <= m; ++j)
{
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
一维数组优化实现
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
−
1
]
[
j
−
v
[
i
]
]
+
w
[
i
]
)
\large f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i])
f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i])
由状态转移方程,可得
f
[
i
]
[
j
]
f[i][j]
f[i][j] 都是由
[
i
−
1
]
[i - 1]
[i−1] 更新过来的,故省略一个维度,仅保留
[
j
]
[j]
[j] 的背包容量的维度。
即变为 f [ j ] = m a x ( f [ j ] , f [ j − v [ i ] ] + w [ i ] ) f[j] = max(f[j],f[j - v[i]] + w[i]) f[j]=max(f[j],f[j−v[i]]+w[i]) ,时间复杂度不变,但空间复杂度减少。由于要满足 i f ( j > = v [ i ] ) if (j >= v[i]) if(j>=v[i]) 条件,只需让 j j j 从 w [ i ] w[i] w[i] 开始遍历。
由于二维数组中状态计算都是由上一行的数据更新过来,即都是从左上方更新过来的。
如图:
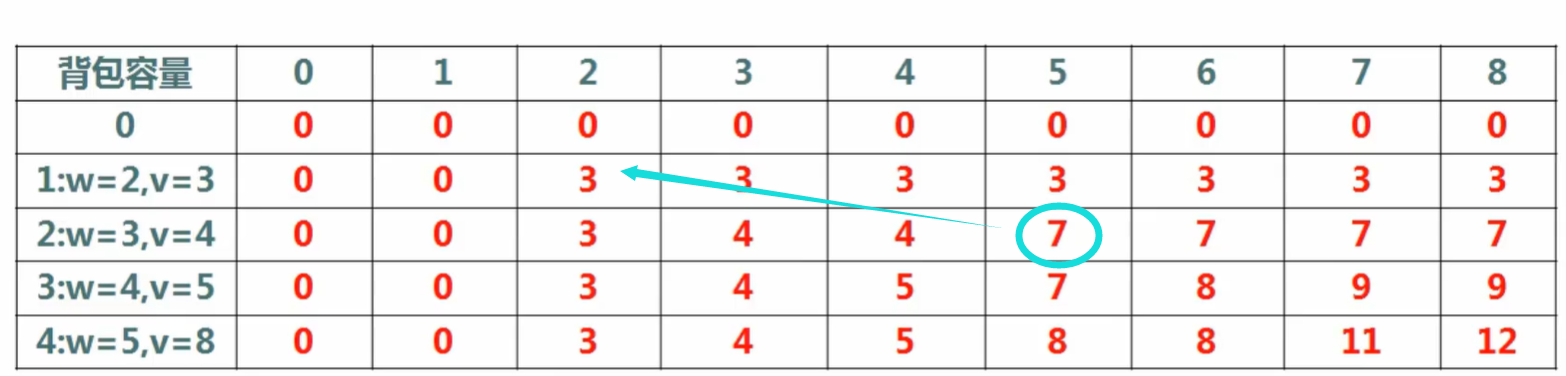
由于优化为了一维数组,可看作二维数组被压缩为了一行,这个时候若是保留二维度数组的从左向右更新模式,就会导致左边数值被提前更新。
如果用二维数组来看的话其更新模式如图:
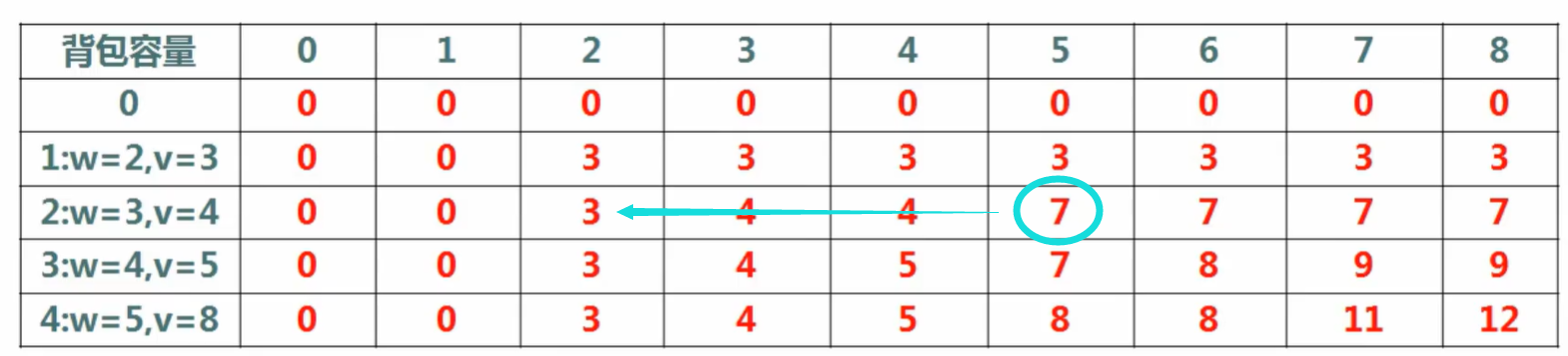
从图可知这样更新会出错误
因此要改变更新模式,改为从右边往左的更新方式,这样每回更新所用到的右边数据就都是没有更新过的数据。
代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int v[N], w[N], f[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> v[i] >> w[i];
for (int j = m; j >= v[i]; --j) // 满足if (j >= v[i])条件,同时改变遍历方向
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
扩展:记忆化搜索 + DPS 实现
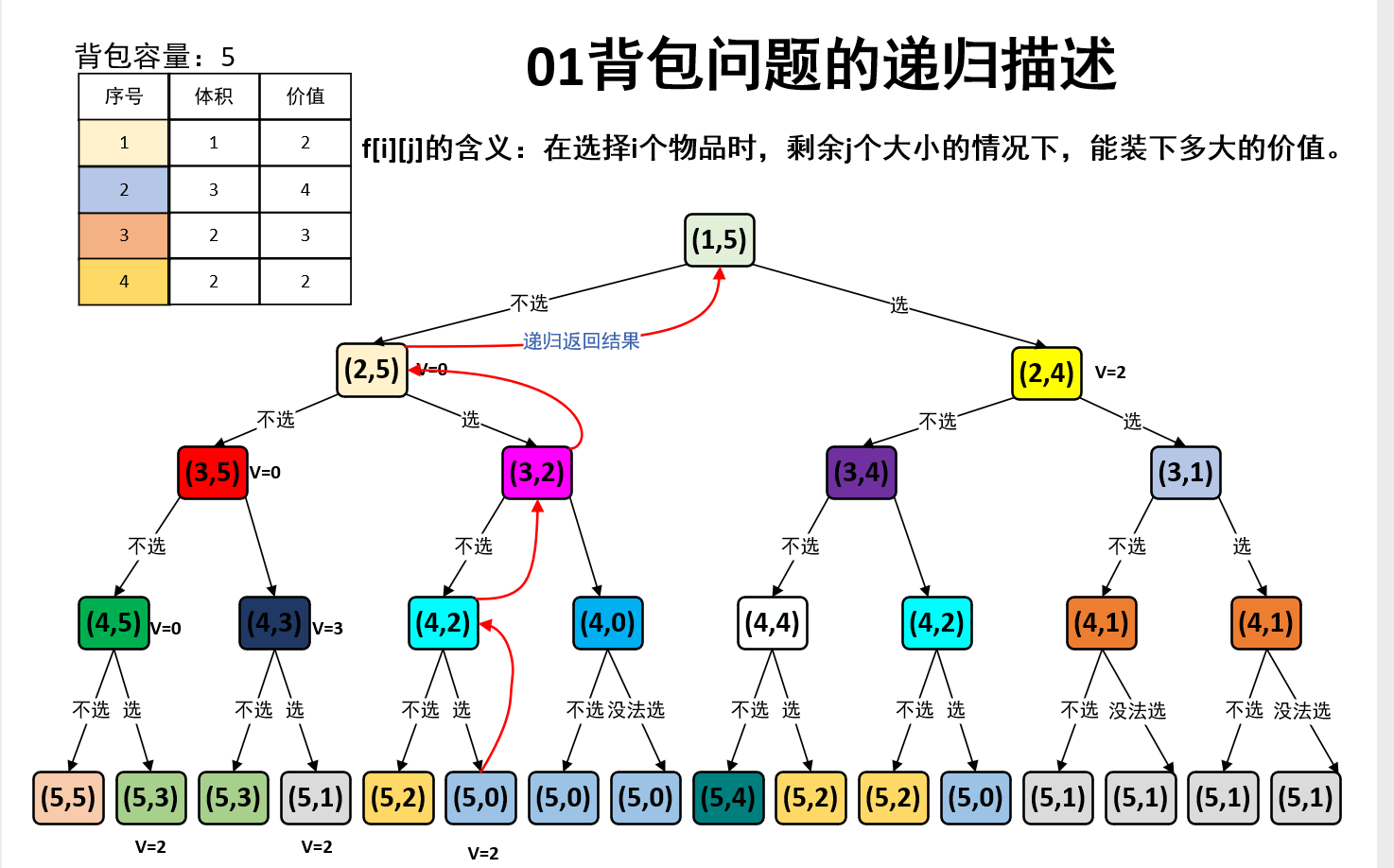
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int n, m, f[N][N], w[N], v[N];
int dfs(int u, int r)
{
if (~f[u][r]) return f[u][r];
if (u == n + 1) return 0;
if (v[u] <= r) return f[u][r] = max(dfs(u + 1, r), dfs(u + 1, r - v[u]) + w[u]);
return f[u][r] = dfs(u + 1, r);
}
int main()
{
cin >> n >> m;
memset(f, -1, sizeof f);
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
cout << dfs(1, m) << endl;
return 0;
}
01背包之恰好装满
有 n n n 个体积和价值分别为 v i , w i v_i,w_i vi,wi 的物品,现从这些物品中挑选出总体积 恰好 为 m m m 的物品,求所有方案中价值总和的最大值。
输入:包含多组测试用例,每一例的开头为两位整数 n 、 m n、m n、m( 1 ≤ n ≤ 10000 , 1 ≤ m ≤ 1000 1 \leq n \leq 10000,1 \leq m \leq 1000 1≤n≤10000,1≤m≤1000),接下来有 n n n 行,每一行有两位整数 v i 、 w i v_i、w_i vi、wi( 1 ≤ v i ≤ 10000 , 1 ≤ w i ≤ 100 1 \leq v_i \leq 10000,1 \leq w_i \leq 100 1≤vi≤10000,1≤wi≤100)。
输出:为一行,即所有方案中价值总和的最大值。若不存在刚好填满的情况,输出 −1。
测试用例:
3 4
1 2
2 5
2 1
3 4
1 2
2 5
5 1
答案:
6
-1
思路
| 前序状态 f[i−1][j] | 前序状态 f[i−1][j−w[i]] | 当前状态 f[i][j] | 转移来源 |
|---|---|---|---|
| 有效状态(满) | 有效状态(满) | 有效状态(满) | m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − w [ i ] ] + v [ i ] ) max(f[i−1][j],f[i−1][j−w[i]]+v[i]) max(f[i−1][j],f[i−1][j−w[i]]+v[i]) |
| 无效状态(不满) | 有效状态(满) | 有效状态(满) | m a x ( f [ i − 1 ] [ j − w [ i ] ] + v [ i ] , − I N F ) max(f[i−1][j−w[i]]+v[i],−INF) max(f[i−1][j−w[i]]+v[i],−INF) |
| 有效状态(满) | 无效状态(不满) | 有效状态(满) | m a x ( f [ i − 1 ] [ j ] , − I N F ) max(f[i−1][j],−INF) max(f[i−1][j],−INF) |
| 无效状态(不满) | 无效状态(不满) | 无效状态(不满) | f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − w ] + v ) f[i][j]=max(f[i−1][j],f[i−1][j−w]+v) f[i][j]=max(f[i−1][j],f[i−1][j−w]+v), − I N F −INF −INF 会被加上 v v v,不再是 − I N F −INF −INF,但肯定是负数。 |
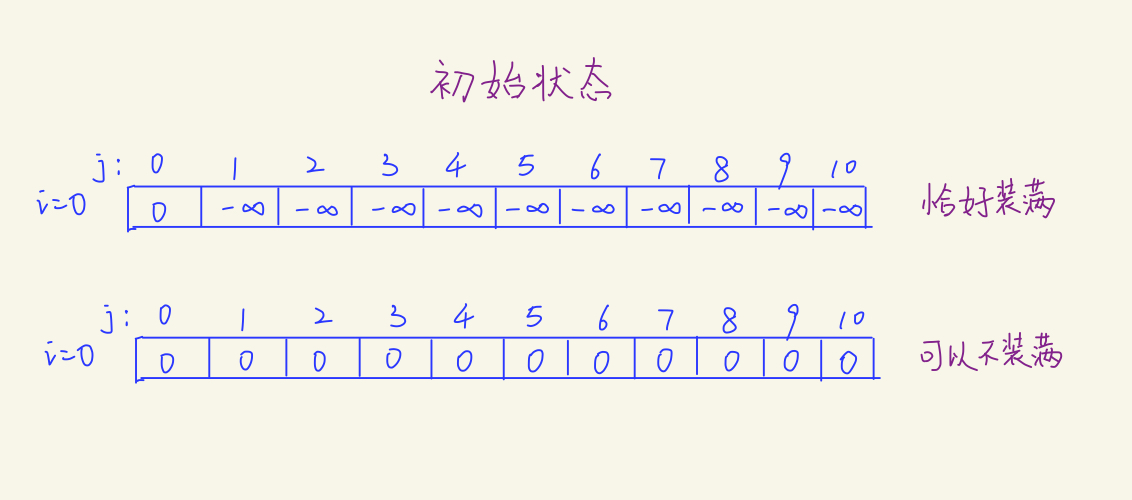
恰好装满:
-
求最大值时,除了 f [ 0 ] f[0] f[0] 为 0 0 0,其他都初始化为无穷小
-0x3f3f3f3f。 -
求最小值时,除了 f [ 0 ] f[0] f[0] 为 0 0 0,其他都初始化为无穷大
0x3f3f3f3f。
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N], v[N], w[N];
int main()
{
int n, m;
while (cin >> n >> m)
{
memset(f, -0x3f, sizeof f);
for (int i = 0; i < N; ++i) f[i][0] = 0;
for (int i = 1; i <= n; ++i)
{
cin >> v[i] >> w[i];
for (int j = m; j >= v[i]; --j)
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
if (f[n][m] < 0) cout << -1 << endl;
else cout << f[n][m] << endl;
}
return 0;
}
完全背包问题
典型例题
题目描述:
有
N
N
N 种物品和一个容量是
V
V
V 的背包,每种物品都有无限件可用。
第 i i i 种物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i,w_i vi,wi,用空格隔开,分别表示第 i i i 种物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N , V ≤ 1000 0<N,V≤1000 0<N,V≤1000
0 < v i , w i ≤ 1000 0<v_i,w_i≤1000 0<vi,wi≤1000
输入样例:
4 5
1 2
2 4
3 4
4 5
输出样例:
10
思路分析
与01背包问题的思路大体相同, 主要在状态的计算方面有所不同,由于完全背包问题下所有可以选用的物品数量是无限的。因此状态转移方程为: f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] + w [ i ] , . . . , f [ i − 1 ] [ j − k ∗ v [ i ] ] + k ∗ w [ i ] ) f[i][j] = max(f[i - 1][j],f[i-1][j - v[i]]+w[i],...,f[i-1][j-k * v[i]]+k*w[i]) f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i],...,f[i−1][j−k∗v[i]]+k∗w[i])
由于 f [ i ] [ j − v [ i ] ] = m a x ( f [ i − 1 ] [ j − v [ i ] ] , f [ i − 1 ] [ j − 2 ∗ v [ i ] ] + w [ i ] , . . . , f [ i − 1 ] [ j − k ∗ v [ i ] ] + k ∗ w [ i ] ) f[i][j-v[i]] = max(f[i - 1][j-v[i]],f[i-1][j - 2*v[i]]+w[i],...,f[i-1][j-k * v[i]]+k*w[i]) f[i][j−v[i]]=max(f[i−1][j−v[i]],f[i−1][j−2∗v[i]]+w[i],...,f[i−1][j−k∗v[i]]+k∗w[i])
为什么最后一项不是 f [ i − 1 ] [ j − ( k + 1 ) ∗ v [ i ] ] + ( k + 1 ) ∗ w [ i ] f[i-1][j-(k+1) * v[i]]+(k+1)*w[i] f[i−1][j−(k+1)∗v[i]]+(k+1)∗w[i] ?
- 这是因为 k k k 的值只与背包最大容量相关
由上面两个公式我们可以推导出:
f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i ] [ j − v [ i ] ] ) f[i][j] = max(f[i - 1][j], f[i][j-v[i]]) f[i][j]=max(f[i−1][j],f[i][j−v[i]])
二维数组代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N], w[N], v[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> v[i] >> w[i];
for (int j = 0; j <= m; ++j)
{
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
一维数组优化实现
由状态转移方程:
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
]
[
j
−
v
[
i
]
]
)
f[i][j] = max(f[i - 1][j], f[i][j-v[i]])
f[i][j]=max(f[i−1][j],f[i][j−v[i]])
类似于01背包问题的一维优化,但是由于 f [ i ] [ j − v [ i ] ] f[i][j-v[i]] f[i][j−v[i]] 是从数组中同行的左边数据更新而来,因此遍历方向只能从左向右,使用左边已被更新后的数据来更新右边的数据。
达到如下图的更新效果:

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 1010;
int f[N], w[N], v[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> v[i] >> w[i];
for (int j = v[i]; j <= m; ++j) f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
多重背包问题
多重背包问题的三种解法
注:
- n 表示物品个数
- V 表示背包的容量
| ① 朴素版本 | ② 二进制优化版本 | ③ 单调队列优化版本 |
|---|---|---|
| n ≤ 100 , V ≤ 100 n≤100,V≤100 n≤100,V≤100 | n ≤ 1000 , V ≤ 2000 n≤1000,V≤2000 n≤1000,V≤2000 | n ≤ 1000 , V ≤ 20000 n≤1000,V≤20000 n≤1000,V≤20000 |
朴素解法
典型题目
题目描述:
有
N
N
N 种物品和一个容量是
V
V
V 的背包。
第 i i i 种物品最多有 s i s_i si 件,每件体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式:
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行三个整数 v i , w i , s i v_i,w_i,s_i vi,wi,si,用空格隔开,分别表示第 i i i 种物品的体积、价值和数量。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0
<
N
,
V
≤
100
0<N,V≤100
0<N,V≤100
0
<
v
i
,
w
i
,
s
i
≤
100
0<v_i,w_i,s_i≤100
0<vi,wi,si≤100
输入样例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
思路
二维数组代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 110;
int f[N][N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j <= m; ++j)
for (int k = 0; k <= s && k * v <= j; ++k) // 遍历第i个物品的所有选取情况
f[i][j] = max(f[i][j], f[i - 1][j - k * v] + w * k);
}
cout << f[n][m] << endl;
return 0;
}
一维数组优化实现
注意:一维化后从右向左遍历。
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 110;
int f[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
int v, w, s;
cin >> v >> w >> s;
for (int j = m; j >= v; --j) // 注意从右向左遍历
{
for (int k = 0; k <= s && k * v <= j; ++k)
f[j] = max(f[j], f[j - k * v] + k * w);
}
}
cout << f[m] << endl;
return 0;
}
二进制解法
典型题目
题目描述:
有
N
N
N 种物品和一个容量是
V
V
V 的背包。
第 i i i 种物品最多有 s i s_i si 件,每件体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式:
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行三个整数 v i , w i , s i v_i,w_i,s_i vi,wi,si,用空格隔开,分别表示第 i i i 种物品的体积、价值和数量。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0
<
N
≤
1000
0<N≤1000
0<N≤1000
0
<
V
≤
2000
0<V≤2000
0<V≤2000
0
<
v
i
,
w
i
,
s
i
≤
2000
0<v_i,w_i,s_i≤2000
0<vi,wi,si≤2000
输入样例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
思路
- 对于每种物品,将其数量进行二进制拆分。例如数量为13的物品,可以拆分为1,2,4,6这四个子集。
- 对每种物品的每个子集,将其看作一个新的物品,权值不变,数量变为子集的数量。
- 对这些新的物品进行01背包的动态规划。
- 在进行动态规划时,需要按照子集的数量从小到大的顺序进行遍历,以保证每个子集只被选择一次。
- 最后得到的解即为原问题的最优解。
二维数组代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 12010, M = 2010; // log_2 2000 = 12,得到二进制分解之后的物品数量约为 12*1000
int f[N][M], v[N], w[N];
int main()
{
int n, m, idx = 0;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
int a, b, s;
cin >> a >> b >> s;
// 进行二进制分解
int k = 1;
while (k <= s)
{
idx++;
v[idx] = a * k;
w[idx] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
idx++;
v[idx] = a * s;
w[idx] = b * s;
}
}
n = idx; // 用二进制分解后的物品数量更新当前物品数量
for (int i = 1; i <= n; ++i) // 经典01背包问题解决
{
for (int j = 0; j <= m; ++j)
{
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
一维数组优化实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 12010, M = 2010;
int f[N], w[N], v[N];
int main()
{
int n, m, idx = 0;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
int a, b, s, k = 1;
cin >> a >> b >> s;
while (k <= s)
{
idx++;
v[idx] = a * k;
w[idx] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
idx++;
v[idx] = a * s;
w[idx] = b * s;
}
}
n = idx;
for (int i = 1; i <= n; ++i)
{
for (int j = m; j >= v[i]; --j)
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
分组背包问题
典型例题
题目描述:
有
N
N
N 组物品和一个容量是
V
V
V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 v i j v_{ij} vij,价值是 w i j w_{ij} wij,其中 i i i 是组号, j j j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行有两个整数
N
,
V
N,V
N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N N N 组数据:
每组数据第一行有一个整数 S i S_i Si,表示第 i i i 个物品组的物品数量;每组数据接下来有 S i S_i Si 行,每行有两个整数 v i j , w i j v_{ij},w_{ij} vij,wij,用空格隔开,分别表示第 i i i 个物品组的第 j j j 个物品的体积和价值;
输出格式:
输出一个整数,表示最大价值。
数据范围:
0
<
N
,
V
≤
100
0<N,V≤100
0<N,V≤100
0 < S i ≤ 100 0<S_i≤100 0<Si≤100
0 < v i j , w i j ≤ 100 0<v_{ij},w_{ij}≤100 0<vij,wij≤100
输入样例:
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例:
8
思路分析
二维数组代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 110;
int f[N][N], v[N][N], w[N][N], s[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> s[i];
for (int j = 0; j < s[i]; ++j) cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; ++i)
{
for (int j = 0; j <= m; ++j)
{
for (int k = 0; k < s[i]; ++k)
{
f[i][j] = f[i - 1][j];
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
cout << f[n][m] << endl;
return 0;
}
一维数组优化实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 110;
int f[N], v[N][N], w[N][N], s[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> s[i];
for (int j = 0; j < s[i]; ++j) cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; ++i)
{
for (int j = m; j >= 0; --j) // 由于组内的物体体积无法直接提出,所以将判断情况后置
for (int k = 0; k < s[i]; ++k)
// 后置的判断情况
if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
cout << f[m] << endl;
return 0;
}

![[论文分享]VOLO: Vision Outlooker for Visual Recognition](https://img-blog.csdnimg.cn/66aca6a3aea648df8876cc9df3b44d8d.png)