文章目录
- 504. 七进制数(进制转换)
- 461. 汉明距离(进制转换 / 异或)
- 136. 只出现一次的数字(位运算)
更多 leetcode 题解可参考:【Programming】
504. 七进制数(进制转换)
给定一个整数,将其转化为7进制,并以字符串形式输出。
-
示例 1:
输入: 100
输出: “202”
示例 2: -
输入: -7
输出: “-10” -
注意: 输入范围是 [-1e7, 1e7] 。
class Solution(object):
def convertToBase7(self, num):
"""
:type num: int
:rtype: str
"""
nums = abs(num)
s = ''
# 这里只对大于0的数算 7 进制
while (nums):
a = nums % 7
nums = nums // 7
s = s+ str(a)
if num > 0:
return s[::-1] # 倒序输出计算结果
elif num < 0:
return '-'+s[::-1] # 负数添加一个负号
else:
return '0' # 0 的话直接返回 0
461. 汉明距离(进制转换 / 异或)
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离。
注意:
0 ≤ x, y < 231.
- 示例:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
思路,计算二进制,然后比不同的位置
class Solution(object):
def hammingDistance(self, x, y):
"""
:type x: int
:type y: int
:rtype: int
"""
# 计算二进制逆序(方便后面的高位补0),结果存在列表中,
def bin_num(x):
list1 = []
while(x):
list1.append(x%2)
x = x//2
return list1
bin_x = bin_num(x)
bin_y = bin_num(y)
len_x = len(bin_x)
len_y = len(bin_y)
# 把两个二进制的长度补成一样的
if len_x < len_y:
bin_x.extend([0]*(len_y-len_x))
else:
bin_y.extend([0]*(len_x-len_y))
# 统计不一样的个数
num = 0
for i in range(len(bin_x)):
if bin_x[i]!=bin_y[i]:
num+=1
return num
还有一种比较快的方法是直接计算异或(相同为1,不同为0)
class Solution(object):
def hammingDistance(self, x, y):
"""
:type x: int
:type y: int
:rtype: int
"""
return bin(x^y).count('1')
补充,异或运算的性质
- a ⊕ a = 0
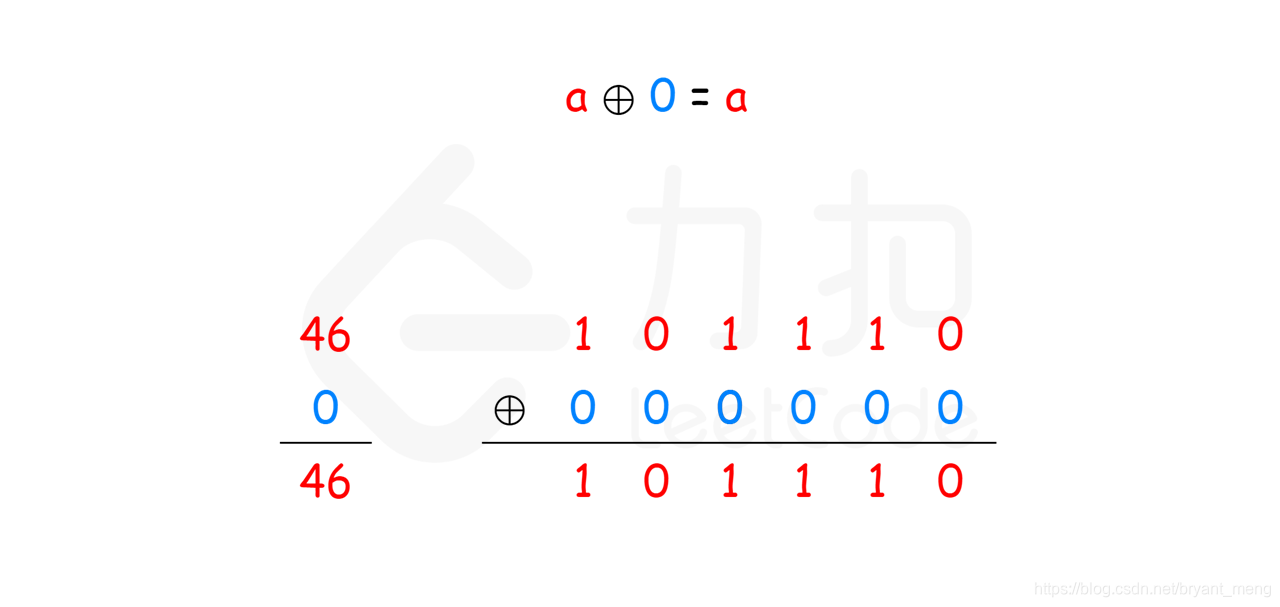
- a ⊕ 0 = a
- a ⊕ b = b ⊕ a,交换律
- a ⊕b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c,结合律
- d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c.
- a ⊕ b ⊕ a = b.
- a ⊕b=b ⊕c => a=b,消去律
相关题目
1720. 解码异或后的数组
136. 只出现一次的数字(位运算)
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
思路:利用异或运算的性质,自己和自己异或结果为 0, 和 0 异或结果为本身

作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/single-number/solution/zhi-chu-xian-yi-ci-de-shu-zi-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
res = 0
for num in nums:
res ^= num
return res