详细内容在这篇论文：Layer Normalization
训练深度神经网络需要大量的计算，减少计算时间的一个有效方法是规范化神经元的活动，例如批量规范化BN（batch normalization）技术，然而，批量规范化对小批量大小（batch size）敏感并且无法直接应用到RNN中（recurrent neural networks），为了解决上述问题，层规范化LN（Layer Normalization）被提出，不仅能直接应用到RNN，还能显著减少训练时间。与批量归一化不同，层规范化直接根据隐藏层内神经元的总输入估计归一化统计数据，因此不会在训练案例之间引入任何新的依赖关系。

背景

A feed-forward neural network is a non-linear mapping from a input pattern $\mathbf{x}$ to an output vector $y$. Consider the $l^{\text{th }}$ hidden layer in a deep feed-forward, neural network, and let $a^l$ be the vector representation of the summed inputs to the neurons in that layer.$a_i^l$是第$l$层第$i$个神经元的线性加权输出。 The summed inputs are computed through a linear projection with the weight matrix $W^l$ and the bottom-up inputs $h^l$ given as follows:
$$a_i^l=w_i^{l^{\top }}{h}^l{h}_i^{l+1}=f\left(a_i^l+b_i^l\right)$$

where $f(\cdot )$ is an element-wise non-linear function（激活函数） and $w_i^l$ is the incoming weights to the $i^{th}$ hidden units and $b_i^l$ is the scalar bias parameter. The parameters in the neural network are learnt using gradient-based optimization algorithms with the gradients being computed by back-propagation.

Batch Normalization

BN是为了减少协变量偏移提出的，它在训练阶段对隐神经元加权输出进行规范化，例如，对于$l^{th}$层的$i^{th}$个加权输出$a_i^l$，BN根据输入数据的分布进行了缩放
$${\bar{a}}_i^l=\frac{g_i^l}{{\sigma }_i^l}\left(a_i^l-{\mu }_i^l\right){\mu }_i^l=\underset{\mathbf{x}\sim P(\mathbf{x})}{\mathbb{E}}\left[a_i^l\right]{\sigma }_i^l=\sqrt{\underset{\mathbf{x}\sim P(\mathbf{x})}{\mathbb{E}}\left[{\left(a_i^l-{\mu }_i^l\right)}^2\right]}$$

where ${\bar{a}}_i^l$ is normalized summed inputs to the $i^{th}$ hidden unit in the $l^{th}$ layer and $g_i$ is a gain parameter scaling the normalized activation before the non-linear activation function.

实际中不会计算真正的$\mu$和$\sigma$，转而去估计一个batch里的$\mu$和$\sigma$，所以BN要求这个batchsize不能太小。然而，在一些在线学习任务以及超大分布模型中往往需要很小的batchsize。

Layer Normalization

$${\mu }^l=\frac{1}{H}\sum _{i=1}^H{a}_i^l{\sigma }^l=\sqrt{\frac{1}{H}\sum _{i=1}^H{\left(a_i^l-{\mu }^l\right)}^2}$$

$H$是一个隐藏层中的隐藏单元数量。在LN中，同一个层共享$\mu$和$\sigma$， but different training cases have different normalization terms. Unlike batch normalization, layer normalization does not impose any constraint on the size of a mini-batch and it can be used in the pure online regime with batch size 1.

In a standard RNN, the summed inputs in the recurrent layer are computed from the current input ${\mathbf{x}}^t$ and previous vector of hidden states ${\mathbf{h}}^{t-1}$ which are computed as ${\mathbf{a}}^t=W_{hh}{h}^{t-1}+W_{xh}{\mathbf{x}}^t$. The layer normalized recurrent layer re-centers and re-scales its activations using the extra normalization terms ：
$${\mathbf{h}}^t=f\left[\frac{\mathbf{g}}{{\sigma }^t}\odot \left({\mathbf{a}}^t-{\mu }^t\right)+\mathbf{b}\right]{\mu }^t=\frac{1}{H}\sum _{i=1}^H{a}_i^t{\sigma }^t=\sqrt{\frac{1}{H}\sum _{i=1}^H{\left(a_i^t-{\mu }^t\right)}^2}$$

where $W_{hh}$ is the recurrent hidden to hidden weights and $W_{xh}$ are the bottom up input to hidden weights. $\odot$ is the element-wise multiplication between two vectors. $\mathbf{b}$ and $\mathbf{g}$ are defined as the bias and gain parameters of the same dimension as ${\mathbf{h}}^t$.

在标准RNN中存在梯度爆炸和消失问题，用了LN之后会更加稳定。
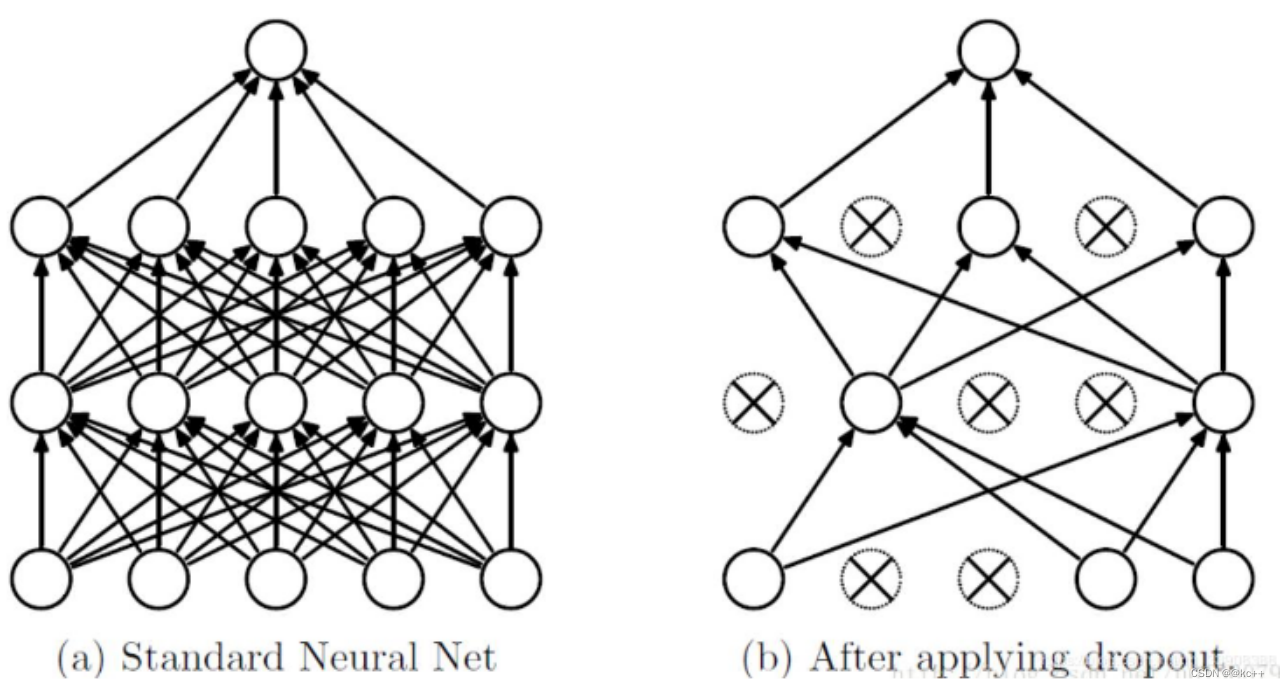
贴两个图便于理解：

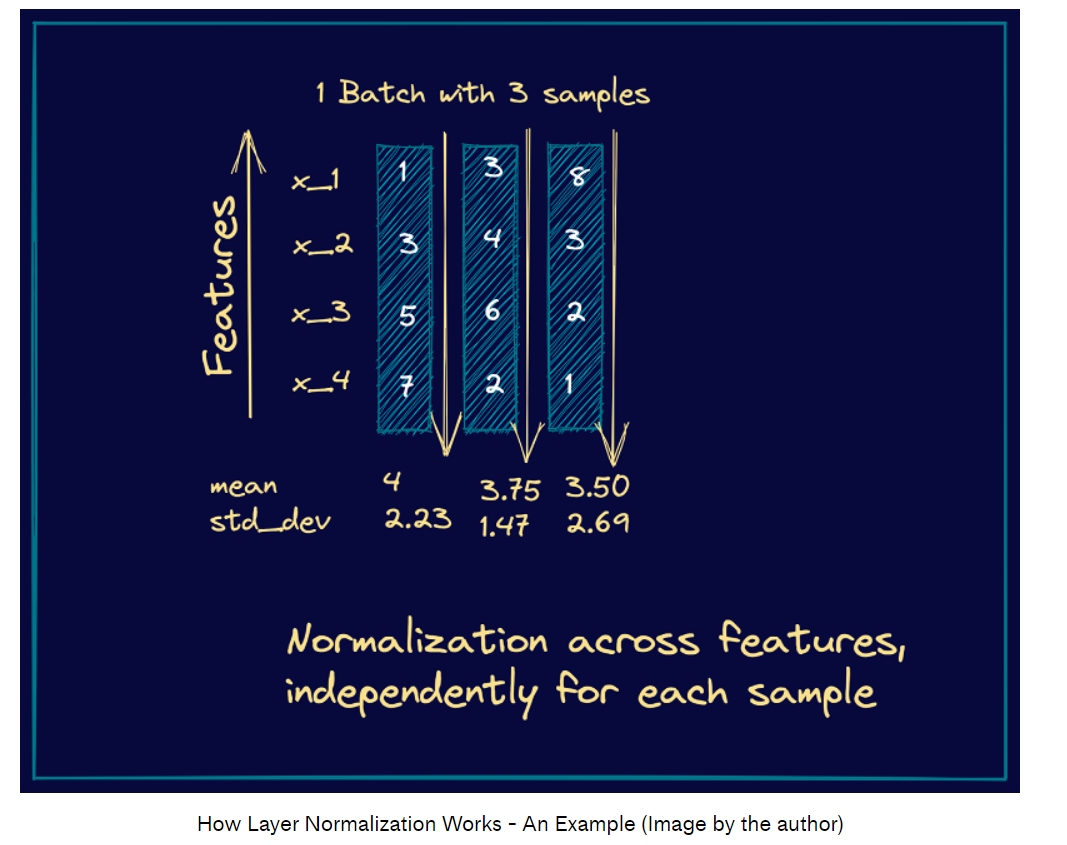
视频讲解可以参考：What is Layer Normalization? | Deep Learning Fundamentals

代码实现

这边贴一个Restormer中的LN层的实现
首先定义两个函数用于reshape。4d到3d不需要参数，因为只需要把已有的两个维度合并；3d到4d需要参数，因为需要把一个维度分成两个维度

def to_3d(x):
    return rearrange(x, 'b c h w -> b (h w) c')

def to_4d(x,h,w):
    return rearrange(x, 'b (h w) c -> b c h w',h=h,w=w)

定义一个没有bias的LN层，weight是可学习的参数，所以用$nn.Parameter$包装

# 没有bias的LayerNorm层
class BiasFree_LayerNorm(nn.Module):
    def __init__(self, normalized_shape):
        super(BiasFree_LayerNorm, self).__init__()
        if isinstance(normalized_shape, numbers.Integral):
            normalized_shape = (normalized_shape,)
        normalized_shape = torch.Size(normalized_shape)

        assert len(normalized_shape) == 1

        self.weight = nn.Parameter(torch.ones(normalized_shape))
        self.normalized_shape = normalized_shape

    def forward(self, x):
    	#x的维度(batch_size, height x width, channels)
    	#sigma的维度(batch_size, height x width, 1)
        sigma = x.var(-1, keepdim=True, unbiased=False)
        return x / torch.sqrt(sigma+1e-5) * self.weight

定义一个有bias的LN层，同样的，weight和bias都是可学习的参数

class WithBias_LayerNorm(nn.Module):
    def __init__(self, normalized_shape):
        super(WithBias_LayerNorm, self).__init__()
        #如果输入的normalized_shape是个整数，则化为元组
        if isinstance(normalized_shape, numbers.Integral):
            normalized_shape = (normalized_shape,)
        normalized_shape = torch.Size(normalized_shape)

        assert len(normalized_shape) == 1

        self.weight = nn.Parameter(torch.ones(normalized_shape))
        #比上面多定义一个bias
        self.bias = nn.Parameter(torch.zeros(normalized_shape))
        self.normalized_shape = normalized_shape

    def forward(self, x):
        mu = x.mean(-1, keepdim=True)
        sigma = x.var(-1, keepdim=True, unbiased=False)
        return (x - mu) / torch.sqrt(sigma+1e-5) * self.weight + self.bias#这边加了bias

把上面的函数包装起来，定义一个统一的层规范化函数

class LayerNorm(nn.Module):
    def __init__(self, dim, LayerNorm_type):
        super(LayerNorm, self).__init__()
        if LayerNorm_type =='BiasFree':
            self.body = BiasFree_LayerNorm(dim)
        else:
            self.body = WithBias_LayerNorm(dim)

    def forward(self, x):
        h, w = x.shape[-2:]
        return to_4d(self.body(to_3d(x)), h, w)