文章目录
- 引言
- 一、回顾
- 二、梳理
- 齐次线性方程组
- 非齐次线性方程组
- 写在最后
引言
两个原因让我想写这篇文章,一是做矩阵题目的时候就发现这三货经常绑在一起,让人想去探寻其中奥秘;另一就是今天学了向量组的秩,让我想起来了之前遗留下来的一个问题:到底存不存在系数矩阵的秩和增广矩阵的秩之差比 1 大的情况?可能这个问题有点抽象,不过看了下面的具体说明应该就能理解了。
一、回顾
问题起因是这样,我在写行列式的文章中关于克莱姆法则应用的说法是这样的:

有读者建议,把方程组无解的情况别写成
r
(
A
)
≠
r
(
A
‾
)
r(A) \ne r(\overline{A})
r(A)=r(A) ,而写成
r
(
A
)
+
1
=
r
(
A
‾
)
r(A) +1 = r(\overline{A})
r(A)+1=r(A) . 我当时还未复习到方程组和向量部分,有这样的疑问:为什么非得是相差 1 ,我如果
A
A
A 有很多行为 0 ,增广矩阵的秩不就可以比系数矩阵大不止 1 吗?
我当时隐约感觉是行秩和列秩模糊的问题。一方面矩阵中,我们比较常用的是初等行变换,忽视了列变换以及列秩,另一方面,列秩在方阵中和行秩是一样的。
起初我也是认为,列秩没什么用的,直到学到了向量这一部分。由于一般我们指的向量是列向量,那么由一个向量组构成的矩阵,自然考虑的是列秩。
因此我们针对一个一般性的 m × n m \times n m×n 矩阵或 n n n 个 m m m 维的向量组进行梳理,请看下文。
二、梳理
对于一般齐次线性方程组:
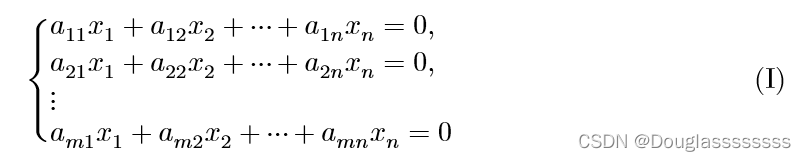
以及一般非齐次线性方程组:
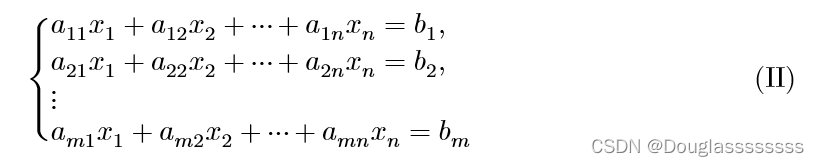
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \alpha_1=(a_{11},a_{21},\dots,a_{m1})^T,\alpha_2=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\alpha_n=(a_{1n},a_{2n},\dots,a_{mn})^T,b=(b_{1},b_{2},\dots,b_{m})^T α1=(a11,a21,…,am1)T,α2=(a12,a22,…,am2)T,…,αn=(a1n,a2n,…,amn)T,b=(b1,b2,…,bm)T ,则方程组(I)(II)可表示为如下向量形式: x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( 1.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0 (1.1) x1α1+x2α2+⋯+xnαn=0(1.1) x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( 2.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (2.1) x1α1+x2α2+⋯+xnαn=b(2.1)
令矩阵
A
=
[
α
1
,
α
2
,
…
,
α
n
]
A=[\alpha_1,\alpha_2,\dots,\alpha_n]
A=[α1,α2,…,αn] ,即

则方程组(I)(II)可表示为如下矩阵形式:
A
(
x
1
,
x
2
,
…
,
x
n
)
T
=
0
(
1.2
)
A(x_1,x_2,\dots,x_n)^T=0(1.2)
A(x1,x2,…,xn)T=0(1.2)
A
(
x
1
,
x
2
,
…
,
x
n
)
T
=
b
(
2.2
)
A(x_1,x_2,\dots,x_n)^T=b(2.2)
A(x1,x2,…,xn)T=b(2.2)
齐次线性方程组
对于齐次线性方程组(I),它有 m m m 个约束方程, n n n 个未知数。首先我们应了解的是,不管方程个数和未知数个数多少,不可能无解,都是存在零解的。我们要讨论,就是讨论有没有非零解。我们分三种情况:
(一) m < n . m < n. m<n.
此时齐次线性方程组约束条件个数小于未知数,必有一个未知数无法受限制,如果那个不受限制的未知数取非零的话,就存在非零解。那么向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 必线性相关,则该向量组的秩 < n <n <n ,根据三秩相等性质, r ( A ) < n . r(A)<n. r(A)<n.
这种情况其实没什么好讨论的,因为肯定存在非零解,所以这也是为什么书上很少提及的情况吧。
(二) m = n . m=n. m=n.
此时就有讨论的必要了,因为方程组可能只有零解,也可能有非零解。
若齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
我们此时可以得出 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0,即因为系数矩阵是方阵且满秩。
若齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
为什么是小于 n n n 呢?因为构成系数矩阵的列向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn的秩小于 n n n ,根据三秩相等性质,该矩阵的秩亦小于 n n n 。
(三) m > n . m > n. m>n.
此时约束方程个数更多,不过不影响什么。系数矩阵的秩仍然是满足 r ( A ) ≤ n , r(A) \leq n, r(A)≤n, 同样有和第 2 种情况一样的的结论。
把这三种情况总结起来,其实还是第二种情况的结论。因此不论是否是方阵,未知数和方程的个数如何,都有如下结论:即
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
非齐次线性方程组
对于非齐次线性方程组(II),它有 m m m 个约束方程, n n n 个未知数,右端常数向量为 b = ( b 1 , b 2 , … , b m ) \pmb{b=(b_1,b_2,\dots,b_m)} b=(b1,b2,…,bm) ,增广矩阵为 A ‾ = [ A ∣ b ] . \overline{A}=[A|b]. A=[A∣b].
我们从其对应的齐次线性方程组(I)出发,若(I)只有零解,根据上述结论,有向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关且 r ( A ) = n . r(A)=n. r(A)=n.
接下来我们讨论此时非齐次的情况,若非齐次线性方程组(II)无解,则向量 b \pmb{b} b 不能被无关的向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 也线性无关,可得 r ( A ‾ ) = n + 1 r(\overline{A})=n+1 r(A)=n+1 . 若非齐方程组(II)有解,则向量 b \pmb{b} b 能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 线性相关,可得 r ( A ‾ ) < n + 1 r(\overline{A})<n+1 r(A)<n+1 . 又因为向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关,故 r ( A ‾ ) = n = r ( A ) . r(\overline{A})=n=r(A). r(A)=n=r(A).
若方程组(II)对应的齐次方程组(I)有非零解,根据前一部分的结论,方程组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关且 r ( A ) < n . r(A)<n. r(A)<n.
我们讨论此时的非齐次方程组(II)的情况,若方程组(II)无解,则向量 b \pmb{b} b 不能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,但由于向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 是线性相关的,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 线性相关,可得 r ( A ‾ ) < n + 1 r(\overline{A})<n+1 r(A)<n+1 且 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
因为向量 b \pmb{b} b 不能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,则向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 的秩比向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 多 1 ,即 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
O.O 这个还是可以直观理解的。向量组是一列一列的,加了一列不能被原来表示的列,肯定秩加了 1 嘛。
若方程组(II)有解,则向量 b \pmb{b} b 能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,故 r ( A ‾ ) = r ( A ) < n . r(\overline{A})=r(A)<n. r(A)=r(A)<n.
如下图所示,讨论了所有情况下的秩的特征

总结一下可以得到如下一般性的结论:
- 非齐次方程组有解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) ≠ r ( A ) , r(\overline{A})\ne r(A), r(A)=r(A), 或 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
有解其实还可以再做讨论,就放在后面方程组那一章再来细说吧。
写在最后
看来还是自己疏忽了三秩相等的性质,才会产生开头那样的疑问。
现在也越来越认同,其实向量才是贯穿线性代数的重要工具。