Ⅰ、直观理解

1、描述

从直观上来看，卡尔曼滤波是把两个存在误差的结果融合在一起，得到一个从数学上可以得到证明的最优估计值。
而这两个存在误差的结果，一个是从理论上推导出来的，称之为先验估计值；一个是用传感器测量出来的，称之为测量值。它们之所以存在误差，是因为前者的理论模型存在现实干扰，后者的测量仪器存在不可避免的精度问题。
图片的具体解释比较复杂，此处可以且看且过。

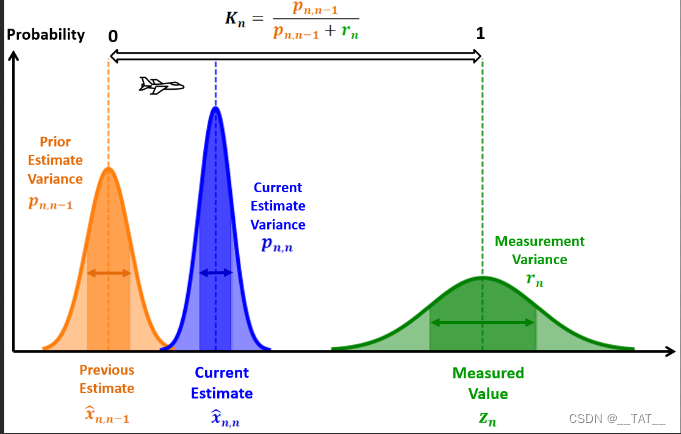
图片解释：以上三个颜色都符合正太分布，其中橙色部分的期望是先验估计值，绿色部分的期望是测量值，蓝色部分的期望便是融合绿色和橙色之后的最优估计值。
Q1：为什么它们都呈现出正太分布呢？
图中橙色部分和绿色部分之所以呈现出正太分布，是因为前者存在过程噪声，后者存在测量噪声的缘故。而这两个噪声被假定为符合正太分布。至于蓝色部分，解释起来就复杂许多，下文再说了。
Q2：噪声从哪里来？
过程噪声正式前文提到的：“理论模型存在现实干扰” 中的现实干扰。测量噪声则是：“测量仪器存在不可避免的精度问题” 中的精度误差。也就是说，以上这个图是在理论之上考虑了现实干扰和仪器误差的图。
Q3：为什么噪声会符合正太分布？
事实上，噪声不可能完美的符合正太分布，只是自然界大多数噪声，甚至许多统计学的例子，都可以被近似为正太分布。比如世界上人的身高、智商、体重等的分布情况，大体上是符合正太分布的。
Q4：过程噪声和测量噪声的方差如何知道？
这是通过工程实际，试出来的，并非理论推导。想PID算法一样，P、I、D这三个量得试出来。这些无法确定的量，被称为超参数。

2、例子

前提：现已知小车当下的位置、速度、加速，并有一卫星实施监测小车的位置。
目标：求小车下一时刻的位置。
分析：从由于存在阻力，人为因素等原因。我们所知道的小车当前位置、速度、加速度存在一定程度的误差。所以利用这些条件求得的小车下一时刻的位置存在偏差。而由于卫星精度的问题，仅仅靠卫星也无法得到小车下一时刻的准确位置。
解决：卡尔曼认为，可以取长补短，综合考虑理论上得出的结果和卫星的测量结果，得出最优解。比如理论上得出的小车下一时刻的位置是10m，卫星得出的是11m。那我们大致可以推断真实的小车位置大概介于10m和11m之间，至于最优解到底因该是多少m，这是卡尔曼滤波要解决的问题，。

Ⅱ、适用范围

1、线性系统

线性系统要求系统同时满足齐次性和可加性。
齐次性：输入扩大N倍，其输出也扩大N倍。

齐次性的数学表达： 如果： y 1 ( t ) = M { f 1 ( t ) } f 2 ( t ) = a f 1 ( t ) 则： y 2 ( t ) = M { f 2 ( t ) } = a y 1 ( t ) \begin{array}{l} 如果：\\{y_1}(t) = M\{ {f_1}(t)\} \\ {f_2}(t) = a{f_1}(t)\\ 则：\\{y_2}(t) = M\{ {f_2}(t)\} = a{y_1}(t) \end{array} 如果：y1​(t)=M{f1​(t)}f2​(t)=af1​(t)则：y2​(t)=M{f2​(t)}=ay1​(t)​

可加性：N个输入，输出等于N个输入独立的输出之和。

可加性的数学表达： 如果 : y 1 ( t ) = M { f 1 ( t ) } y 2 ( t ) = M { f 2 ( t ) } 且 : f 3 ( t ) = f 1 ( t ) + f 2 ( t ) y 3 ( t ) = M { f 3 ( t ) } 则 : y 3 ( t ) = y 1 ( t ) + y 2 ( t ) \begin{array}{l} 如果:\\ {y_1}\left( t \right) = M\{ {f_1}\left( t \right)\} \\ {y_2}\left( t \right) = M\{ {f_2}\left( t \right)\} \\ 且:\\ {f_3}\left( t \right) = {f_1}\left( t \right) + {f_2}\left( t \right)\\ {y_3}\left( t \right) = M\left\{ {{f_3}\left( t \right)} \right\}\\ 则:\\ {y_3}\left( t \right) = {y_1}\left( t \right) + {y_2}\left( t \right) \end{array} 如果:y1​(t)=M{f1​(t)}y2​(t)=M{f2​(t)}且:f3​(t)=f1​(t)+f2​(t)y3​(t)=M{f3​(t)}则:y3​(t)=y1​(t)+y2​(t)​

简而言之：线性系统满足”和的响应等于响应的和“。

2、噪声服从高斯分布

高斯分布又称正态分布，而前文提到自然界中许多噪声都可以近似为正态分布，所以在一般情况下这个条件是满足的。

一维正态分布表达式：$P(a)-N\left(u,{\partial }^2\right)$

二维正态分布表达式：$P(a)-N\left(u_1,u_2,{{\partial }_1}^2,{{\partial }_2}^2,\rho \right)$

二维正态分布的另一种表达式：$P\left(A\right)-N\left(U,P\right)$
其中A，U分别是一个2x1的系数矩阵，而P则是一个协方差矩阵。如图

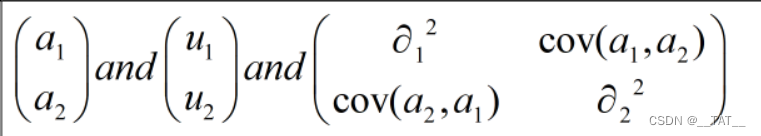
Ⅲ、相关公式

1、原始公式

$i:x_k=A{x}_{k-1}+B{u}_{k-1}+w_{k-1}$
$ii:z_k=H{x}_k-v_k$

即：

i：本次实际值 = 上一次的实际值 + 控制量 + 过程扰动
ii：本次测量值 = 实际值 - 测量误差

如果不加上噪声，那将推导出存在误差的计算值（先验估计值）和测量值。

$i:{{\hat{x}}_k}^{-}=A{\hat{x}}_{k-1}+B{u}_{k-1}$
$ii:{\hat{x}}_{kmea}=H^{-}{z}_k$

即：

i：本次计算值 = 上一此最优估计值+ 控制量
ii：本次测量值 = 转化关系 x 本次传感器测量值

$x_k$是实际的目标状态的值，${{\hat{x}}_k}^{-}$表示先验估计值，${\hat{x}}_{kmea}$表示测量值。A表示状态转移矩阵，${\hat{x}}_{k-1}$表示上一次的最优估计值，B表示控制矩阵，$u_{k-1}$表示控制变量（即输入），$w_k$表示过程噪音，$z_k$表示传感器的测量值，H表示$z_k$和${\hat{x}}_{mea}$之间的关系矩阵，$v_k$表示测量噪音。
注：之所以需要H，是因为传感器测量出来的值不一定就是目标值，比如某项任务中，传感器测量出来的是开尔文，但我们需要的是摄氏度之类的。

2、预测公式

$$（1）{{\hat{x}}_k}^{-}=A{\hat{x}}_{k-1}+B{u}_{k-1}$$

$$（2）{P_k}^{-}=A{P}_{k-1}{A}^T+Q$$

（2）中${P_k}^{-}$表示($x_k-{{\hat{x}}_k}^{-}$)的协方差矩阵，$P_k$表示($x_k-{\hat{x}}_k$)的协方差矩阵，Q表示噪音$w_k$的协方差矩阵。

3、更新公式

$$（3）K_k=\frac{{P_k}^{-}{H}^T}{H{P_k}^{-}{H}^T+R}$$

$$（4）{\hat{x}}_k={{\hat{x}}_k}^{-}+K_k\left(Z_k-H{{\hat{x}}_k}^{-}\right)$$

$$（5）P_k=\left(I-K_{k}H\right){P_k}^{-}$$
其中的$K_k\in \left[0,H^{-}\right]${K_k}是卡尔曼增益系数，$I$为单位矩阵，R表示测量噪声$v_k$的协方差矩阵，${\hat{x}}_k$表示最优估计值。

4、初值赋予

一般只要$P_0$不等与零即可，不妨设$x_0$= 0，$P_0$ = 1

5、总结

（4）公式也正是卡尔曼滤波的核心公式，由$\left\{\begin{array}{l}{\hat{x}}_k={{\hat{x}}_k}^{-}+G\left({\hat{x}}_{kmea}-{{\hat{x}}_k}^{-}\right)\\ K_k=GH,G\in \left(0,1\right)\end{array}\right\}$变化而来。
在（4）中，当$K_k$ = $H^{-}$时，${\hat{x}}_k$ = ${{\hat{x}}_k}^{-}$，表示完全相信计算值（即预估值）。同理，当$K_k$ = 0 时，${\hat{x}}_k$ = $H^{-}{z}_k$ = ${\hat{x}}_{mea}$，表示完全相信测量值。而卡尔曼滤波的核心便是寻找合适的$K_k$使得最优估计值${\hat{x}}_k$，它可以在计算值和测量值之间”取长补短“，使${\hat{x}}_k$最接近于真实值。
至于$K_k$如何求，公式（3）已经给出了。而通过公式（2）、（3）也b不难知道由于A、H、$P_k$ 是已知的，所以$K_k$取值最终是多少取决于与超参数Q和R。在上文Ⅰ章节，已经对Q和R做出过解释了。

另外：本小结唐突的给出了卡尔曼滤波的五个公式，其原因是这五个公式背后的推导过于复杂，而且如果不具备相关的数学知识以及控制理论的知识，理解起来也十分费劲，所以不妨先囫囵吞枣的接受，希望接下来的应用举例能有更加直观的理解。

Ⅳ、应用例子

1、前提条件：
条件一、小车在二维平面上以匀加速直线运动（系统满足线性）。
条件二、有一个卫星可以观测小车的位置，每$\Delta t$观测一次。
2、目的
每隔$\Delta t$时间，求一次小车的位置。
3、状态方程和测量方程的构建

其中p表示位置，v表示速度，a是加速度常数，然后下面的$p_{satellite\_k}$是卫星所测量得的数据。其他数据对照本文Ⅲ给出的公式。
以上这两个等式已经给出了A，B，H，$u_k、z_k、{{\hat{x}}_k}^{-}$等参数，接下来只需找到合适的Q和R，便可以带入本文Ⅲ的公式进行运算，完成卡尔曼滤波。

Ⅴ、代码实现

Ⅵ、公式理解

1、协方差矩阵的理解

1.1 协方差

协方差表示两个变量之间的关联程度，数学符号为cov()。在此不妨设有两个数a和b。当a增大时，b也增大。a减小时，b也减小。那么可以认为a和b正相关，其协方差cov(a,b)>0。反之a增大，b减小，那么a和b负相关，cov(a,b)<0。而若a的变化与b的变化毫无关系，则cov(a,b)=0。

协方差的相关性质：
1、cov(a,b)=E{(a-E(a))(b-E(b))}    //这是协方差的原始公式
2、cov(a,b)=E(ab)-E(a)E(b)
3、cov(a+C,b+D)=cov(a,b)   //其中C和D为常数，下同
4、cov(Ca,Db)=CDcov(a,b)
5、cov(a,b)=cov(b,a)

1.2 协方差矩阵

协方差矩阵用于描述多个变量之间的关程度，以及自身的方差。不妨设有三个变量a，b，c，其协方差矩阵为P。P的对角线分别是a，b，c三个变量的方差。其他则存放则三个变量之间的协方差。根据上文的协方差性质5可知，该矩阵为对称矩阵。

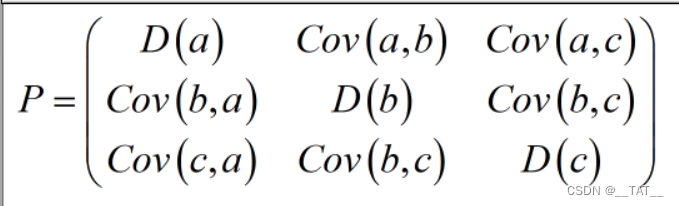
如果a，b，c三个变量没用任何关系，那么P矩阵便可以这样表达。

而再如果a，b，c的期望都为零，那么P矩阵可以进一步这样写。

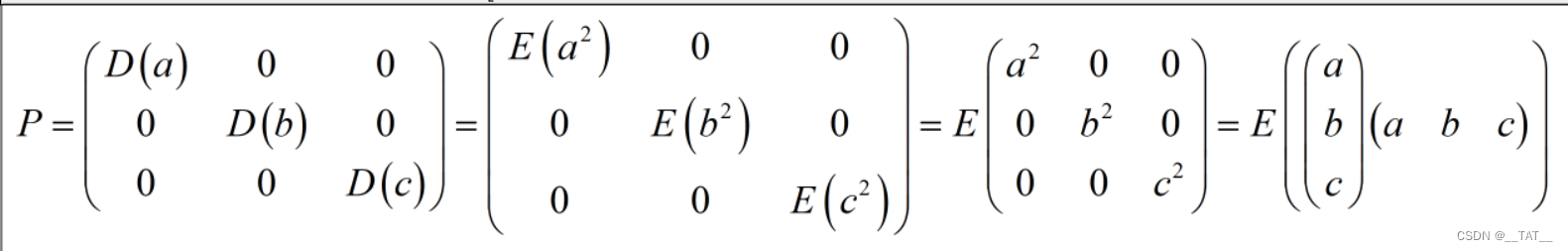
值得注意的是，从宏观的角度来看，协方差矩阵只是在描述一个向量的内部各个变量自身的离散程度和各个变量之间的联系。

1.3、相关数学公式

1、方差公式：$D\left(a\right)=E\left(a^2\right)-E^2\left(a\right)$
2、矩阵性质：
$$k\left(\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& y\end{array}\right)=\left(\begin{array}{ccc}ka& kb& kc\\ kd& ke& kf\\ kg& kh& ky\end{array}\right)$$
备注：之所以写这么一大堆，是因为卡尔曼滤波中的噪声通常是多个的，而这几个噪声一般被视为期望为零且相互独立的正态分布。所以以上的知识在推导卡尔曼滤波的数学公式中至关重要，但仅从应用的角度来说，其实不了解也罢。

2、状态方程的理解

状态方程和输出方程是描述一个系统的两个极为重要的方程，下面以连续型系统为例，讲解一下这两个方程。

$Y\left(s\right)=\frac{1}{s}\left(F\left(s\right)-2Y\left(S\right)\right)\Rightarrow Y\left(s\right)/F\left(s\right)=H\left(s\right)=\frac{1}{s+2}$…
由于现实生活中时间是向前推进的，所以节点1和节点2之间采用的是积分算子$\frac{1}{s}$，因此可以知道节点2的导数正是节点1，故可以设节点1为$x^{\prime }$，节点2为$x$。
如果在节点1建立方程便得到：$x^{\prime }=-2x+f\left(t\right)$，这个方程正式这个系统的状态方程。
而输出方程则是：$y\left(t\right)=x+0f\left(t\right)$
由此可以引出连续系统状态方程和输出方程的通用表达式：

$\begin{array}{l}{x}^{\prime }\left(t\right)=Ax\left(t\right)+Bf\left(t\right)\\ y\left(t\right)=Cx\left(t\right)+Df\left(t\right)\end{array}$
推广到离散系统：
$\begin{array}{l}{x}_{k+1}=A{x}_k+B{f}_k\\ y_k=C{x}_k+D{f}_k\end{array}$