本文是对https://spaces.ac.cn/archives/8847文章的总结

有监督的文本表征主流方案是sentence bert，虽然sentence BERT效果还行，但是存在训练和预测不一致的问题，而一些文章也指出而如果直接优化预测目标cos值，效果往往特别差（如CoSENT（一）：比Sentence-BERT更有效的句向量方案，我也尝试了下，效果貌似不是太差，甚至比sentence bert好一点）

直接优化Cos方案

直接优化cos值通常有如下几种损失函数方案，其中t∈{0,1}表示是否相似，都是让正样本对的相似度尽可能大、负样本对的相似度尽可能小
$$t\cdot (1-\cos (u,v))+(1-t)\cdot (1+\cos (u,v))$$

$$t\cdot (1-\cos (u,v){)}^2+(1-t)\cdot {\cos }^2(u,v)$$

$$t\cdot (1-cos(u,v))+(1-t)\cdot (max(0,cos(u,v)-margin))$$

文章CoSENT（一）：比Sentence-BERT更有效的句向量方案针对直接优化cos效果差，给出如下解释：

文本匹配语料中标注出来的负样本对都是“困难样本”，常见的是语义不相同但字面上有比较多的重合。此时，如果我们用式(1)作为损失函数，那么正样本对的目标是1、负样本对的目标是-1，如果我们用式(2)作为损失函数，那么正样本对的目标是1、负样本对的目标是0。不管哪一种，负样本对的目标都“过低”了，因为对于“困难样本”来说，虽然语义不同，但依然是“相似”，相似度不至于0甚至-1那么低，如果强行让它们往0、-1学，那么通常的后果就是造成过度学习，从而失去了泛化能力，又或者是优化过于困难，导致根本学不动

为了证明上述结论，作者用了如式三所示的损失函数进行验证，margin取0.7，即负样本优化到0.7即不需要继续优化，从而就不那么容易过度学习了。但这仅仅是缓解，效果也很难达到最优，而且如何选取这个margin的值依然是比较困难的问题

Sentence-Bert

sentence-bert采用了训练和预测不一致的方式，它的训练阶段是将u,v,|u−v|（其中|u−v|是指u−v的每个元素都取绝对值后构成的向量）拼接起来做为特征，后面接一个全连接层做2分类（如果是NLI数据集则是3分类），而在预测阶段，还是跟普通的句向量模型一样，先计算句向量然后算cos值作为相似度。如下图所示：

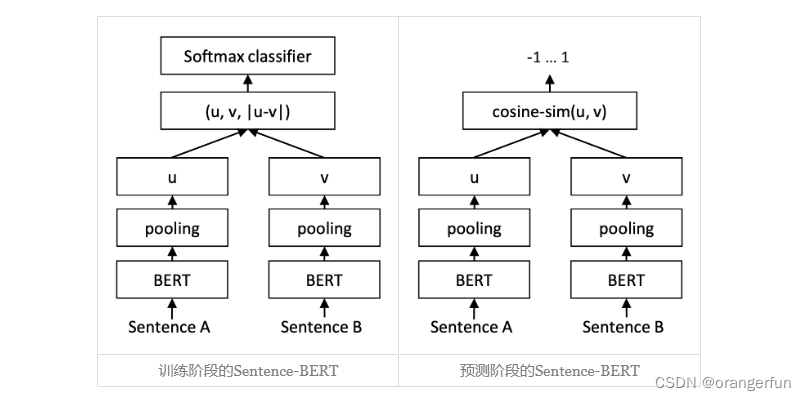
关于sentence-bert的有效性，作者也给出如下思考：

一般情况下，哪怕负样本对是“困难样本”，总体而言正样本对的字面相似度是大于负样本对的，这样一来，哪怕是对于初始模型，正样本对的差距∥u−v∥总体较小，而负样本对的差距∥u−v∥总体较大，我们可以想象正样本对的u−v主要分布在一个半径较小的球面附近，而负样本对的u−v分布在一个半径较大的球面附近，也就是说，初始阶段u−v本身就有聚类倾向，我们接下来只需要根据标签信息强化这种聚类倾向，使得正样本对的u−v依然保持更小，负样本对的u−v保持更大。一个直接的做法就是u−v后面接一个Dense分类器，然而常规的分类器是基于内积的，它没法区分两个分布在不同球面的类别，所以我们加上绝对值变成|u−v|，将球面变为局部的球盖（或者说将球体变成锥形），此时就可以用Dense分类层来分类了。这就是笔者认为的|u−v|的来源。

CoSENT

cosent的提出目标是直接优化cos值，记${\Omega }_{\text{pos }}$为所有的正样本对集合，${\Omega }_{\text{neg }}$为所有的负样本对集合，我们希望对于任意的正样本对$(i,j)\in {\Omega }_{pos}\overline{}$和负样本对$(k,l)\in {\Omega }_{neg}\overline{}$，都有

$$\cos \left(u_i,u_j\right)>\cos \left(u_k,u_l\right)$$

其中$u_i{u}_j{u}_k{u}_l$是各自的句向量，也就是我们只希望正样本对的相似度大于负样本对的相似度，至于大多少，模型自己决定就好。

因此可以使用如下损失, 其中$s_i$是负样本对的相似度，$s_j$是正样本对的相似度

$$loss=\log \left(1+\sum _{i\in {\Omega }_{neg},j\in {\Omega }_{pos}}{e}^{s_i-s_j}\right)$$

上式的由来可参考将“softmax+交叉熵”推广到多标签分类问题，本文在此处略微介绍：
分类任务中交叉熵损失如下：

$$-\log \frac{e^{st}}{{\sum }_{i=1}^n{e}^{s_i}}=-\log \frac{1}{{\sum }_{i=1}^n{e}^{s_i-s_t}}=\log \sum _{i=1}^n{e}^{s_i-s_t}=\log \left(1+\sum _{i=1,i\ne t}^n{e}^{s_i-s_t}\right)$$

而上式又可有如下近似

$$\log \left(1+\sum _{i=1,i\ne t}^n{e}^{s_i-st}\right)\approx \max \left(\begin{array}{c}0\\ s_1-s_t\\ ⋮\\ s_{t-1}-s_t\\ s_{t+1}-s_t\\ ⋮\\ s_n-s_t\end{array}\right)$$

所有的非目标类得分$s_1,\cdots ,s_{t-1},s_{t+1},\cdots ,s_n$跟目标类得分$s_t$两两作差比较，它们的差的最大值都要尽可能小于零，所以实现了“目标类得分都大于每个非目标类的得分”的效果

简单来说，就是如果你希望最终实现$s_i<s_j$，那么就往log里边加入$e^{s_i-s_j}$一项。所以最后可以得到CoSENT损失函数形式如下：

$$cosent\_loss=\log \left(1+\sum _{(i,j)\in {\Omega }_{\text{pos }},(k,l)\in {\Omega }_{\text{neg }}}{e}^{\lambda \left(\cos \left(u_k,u_l\right)-\cos \left(u_i,u_j\right)\right)}\right)$$

其中λ>0是一个超参数，实验中作者取了20。CoSENT损失函数的含义就是：在一个batch中任意一个负样本对的相似度都要小于任意一个正样本对的相似度

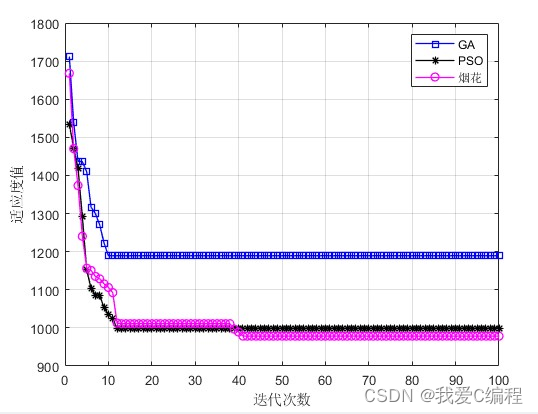
实验结果

下图展示了作者所作的实验，可见CoSENT的优异结果

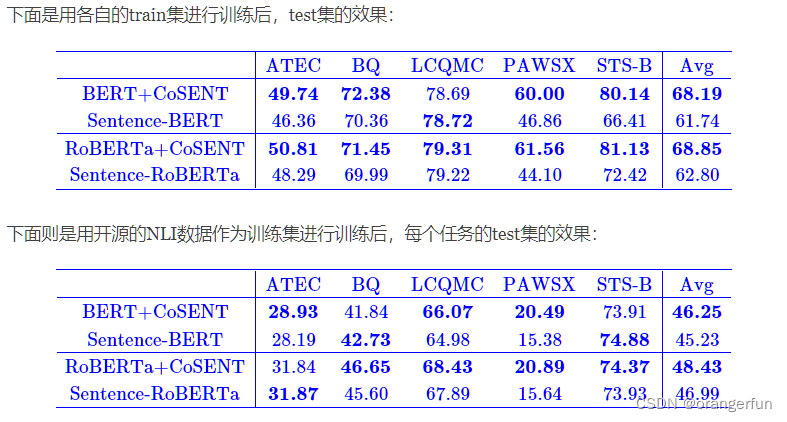
代码实现

from torch import nn
import torch
import torch.nn.functional as F

class CoSENTLoss(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, embed1, embed2, label):
        if type(label) == list:
            label = torch.tensor(label, device=embed1.device)
        # 单位化
        norm_embed1 = F.normalize(embed1, p=2, dim=1, eps=1e-8)
        norm_embed2 = F.normalize(embed2, p=2, dim=1, eps=1e-8)
        # 计算相似度 shape=(batch_size, )
        sim = torch.sum(norm_embed1*norm_embed2, dim=1)*20
        # sim[:, None]改变形状(n, 1), sim[None, :]改变形状(1, n)
        # sim.shape = [bs, bs], 任意相似相减,计算si-sj
        sim = sim[:, None]-sim[None, :]
        # 确定si-sj时si是负样本，sj是正样本;但满足该条件时结果为1
        label = label[:, None]<label[None, :]
        label = label.float()
        # label为0的位置对应的si为正样本, 将该位置为极小的一个数x[-1e12],最终e^(-x)为0忽略不计
        sim = sim-(1-label)*1e12
        # 最前面加一个0元素，通过指数函数后得到对应公式中的1
        sim = torch.cat((torch.zeros(1).to(sim.device), sim.view(-1)), dim=0)
        # 最后求log sum exp
        loss = torch.logsumexp(sim, dim=0)
        return loss


if __name__ == "__main__":
    embed_a = torch.rand(4, 10)
    embed_b = torch.rand(4, 10)
    label = [1, 0, 1, 0]
    cosent_loss = CoSENTLoss()
    loss_value = cosent_loss(embed_a, embed_b, label)
    print(loss_value.item())

参考

CoSENT（一）：比Sentence-BERT更有效的句向量方案
将“softmax+交叉熵”推广到多标签分类问题