目录
摘要部分
张量分解
超平面投影
超平面
投影
超平面投影的应用
数学表示
正则化
引言部分
TKG嵌入方法
举例
相关工作
SKG嵌入方法
评判事实合理性的评分函数模型
平移模型
TransE
TransE例子
张量分解模型
RESCAL
神经网络模型
TKG嵌入方法
外推
插值
具有语义属性的KG嵌入
方法
摘要部分
通过加强关系约束来保留TKG中暗含的语义属性。
借鉴张量分解和超平面投影的思想设计与时间戳关联的关系约束。
采用合适的正则化方案来适应特定的关系约束。
张量分解
张量分解(Tensor Decomposition)是一种数学技术,用于将高维数据结构(称为张量)分解为多个低维组件。张量是一个多维数组,可以看作是矩阵(二维数组)的高维推广。张量分解的目的是找到原始数据的紧凑表示,通常用于数据压缩、降维、特征提取和模式识别等。
常见的张量分解的方法:
-
CP分解(Candecomp/Parafac Decomposition):CP分解将张量分解为一组秩-1张量的和。对于三维张量,CP分解可以表示为三个矩阵的外积和。
-
Tucker分解:Tucker分解将张量分解为一个核心张量和一组矩阵的乘积。与CP分解不同,Tucker分解允许核心张量具有不同的秩。
-
张量奇异值分解(Tensor SVD):这是奇异值分解(SVD)的张量推广,用于将张量分解为一组正交矩阵和一组奇异值。
-
分层Tucker分解(Hierarchical Tucker Decomposition):这种方法采用分层结构来分解张量,允许更灵活和可扩展的表示。
超平面投影
超平面
超平面是一个维度比包围空间低一维的子空间。例如,在三维空间中,超平面是一个平面;在二维空间中,超平面是一条直线。
投影
投影是将一个点或一组点从一个空间映射到另一个空间的过程。在超平面投影的情况下,这意味着将高维空间中的点映射到一个低维子空间上。
超平面投影的应用
超平面投影在许多领域都有应用,包括:
-
降维:通过将数据投影到低维子空间,可以减少数据的复杂性和维度,同时保留重要的特征和结构。
-
分类和回归:在支持向量机(SVM)等机器学习算法中,超平面用作决策边界,将不同类别的数据分开。
-
数据可视化:通过将高维数据投影到二维或三维空间,可以更容易地可视化和理解数据的结构和关系。
数学表示
超平面可以通过线性方程来表示:
其中 是超平面的法向量,
是常数,
是空间中的点。
投影点可以通过以下公式计算:
其中 是投影点,
是原始点,
是超平面上的任意点,
是超平面的法向量。
超平面投影是一种强大的数学工具,用于降维、分类、回归和数据可视化。它通过将高维空间中的点投影到低维子空间来实现这些目的,从而提供了一种有效的方式来分析和解释复杂数据集。
正则化
正则化(Regularization)是机器学习和统计建模中的一个技术,用于防止模型过拟合。过拟合是指模型在训练数据上表现得非常好,但在未见过的测试数据上表现较差的现象。正则化通过向模型的目标函数(通常是损失函数)添加一个惩罚项来实现。
正则化的基本思想是限制模型的复杂度,使其不会过于依赖训练数据中的噪声或异常值。通过引入一些形式的惩罚,正则化鼓励模型选择较小的参数值,从而使模型更简单、更平滑。
常见的正则化方法有:
- L1正则化:也称为Lasso正则化,通过在损失函数中添加参数的绝对值之和作为惩罚项。这通常会导致某些参数精确为零,从而实现特征选择。
- L2正则化:也称为岭回归(Ridge Regression),通过在损失函数中添加参数的平方和作为惩罚项。这有助于防止参数值过大。
- Elastic Net正则化:结合L1和L2正则化,既实现了特征选择,又防止了参数过大。
其中,是正则化强度的超参数,通过交叉验证等方法选择合适的值。
正则化有助于提高模型的泛化能力,使其在未见过的数据上表现得更好。不过,选择合适的正则化方法和强度需要仔细的调整,以便在偏差和方差之间找到合适的平衡点。
引言部分
TKG嵌入方法
被证明在进行时序知识图谱补全时是有用的。
这些方法通常通过将时间戳信息合并到现有的评分函数中来扩展针对静态知识图设计的嵌入方法。
这些方法主要注意于测量整个事实的合理性,而忽略了每个实体在特定时间戳上出现在关系的主体或对象位置上的偏差。
举例
相关工作
根据是否考虑了时间信息,相关模型分为两类:静态知识图谱(SKG)嵌入方法,时序知识图谱(TKG)嵌入方法
SKG嵌入方法
实体和关系被嵌入到连续的低维向量空间中。
评判事实合理性的评分函数模型
-
平移模型
TransE
TransE 是一种基本的平移模型,它将该关系看作是从嵌入的主体实体到嵌入的对象实体的几何平移。
TransE的核心思想是将知识图谱中的三元组(头实体、关系、尾实体)表示为向量空间中的平移操作。具体来说,如果一个三元组(h, r, t)是真实的(即存在于知识图谱中),那么头实体的向量表示与关系的向量表示
之和应该接近尾实体的向量表示
。数学上,这可以表示为:
TransE的目标是学习实体和关系的向量表示,使得真实三元组的这一约束得到满足,同时不真实的三元组(即不在知识图谱中的三元组)不满足该约束。
为了实现这一目标,TransE使用了一个损失函数,通常是基于间隔的合页损失(margin-based hinge loss)。损失函数鼓励真实三元组的得分低于不真实三元组的得分,并且两者之间的差距至少为一个预定的间隔。
TransE例子
import torch
import torch.nn as nn
import torch.optim as optim
# 定义实体和关系
entities = ["北京", "纽约", "巴黎", "中国", "美国", "法国"]
relations = ["位于"]
entity2idx = {entity: idx for idx, entity in enumerate(entities)}
relation2idx = {relation: idx for idx, relation in enumerate(relations)}
# 定义三元组
triples = [
("北京", "位于", "中国"),
("纽约", "位于", "美国"),
("巴黎", "位于", "法国"),
]
# 超参数
embedding_dim = 10
margin = 1.0
learning_rate = 0.01
epochs = 1000
# 初始化实体和关系的嵌入
entity_embeddings = nn.Embedding(len(entities), embedding_dim)
relation_embeddings = nn.Embedding(len(relations), embedding_dim)
# 优化器
optimizer = optim.SGD(list(entity_embeddings.parameters()) + list(relation_embeddings.parameters()), lr=learning_rate)
# 训练
for epoch in range(epochs):
total_loss = 0
for head, relation, tail in triples:
# 获取实体和关系的索引
head_idx = torch.LongTensor([entity2idx[head]])
relation_idx = torch.LongTensor([relation2idx[relation]])
tail_idx = torch.LongTensor([entity2idx[tail]])
# 获取嵌入
head_embedding = entity_embeddings(head_idx)
relation_embedding = relation_embeddings(relation_idx)
tail_embedding = entity_embeddings(tail_idx)
# 计算损失
loss = torch.nn.functional.relu(margin + (head_embedding + relation_embedding - tail_embedding).norm(p=1) - (head_embedding + relation_embedding - tail_embedding).norm(p=1))
total_loss += loss.item()
# 反向传播和优化
loss.backward()
optimizer.step()
optimizer.zero_grad()
if epoch % 100 == 0:
print(f"Epoch {epoch}, Loss: {total_loss}")
# 打印最终的嵌入
print("Entity embeddings:", entity_embeddings.weight.data)
print("Relation embeddings:", relation_embeddings.weight.data)
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 使用PCA将实体嵌入降到2维
pca = PCA(n_components=2)
entity_embeddings_2d = pca.fit_transform(entity_embeddings.weight.data)
# 绘制实体
plt.scatter(entity_embeddings_2d[:, 0], entity_embeddings_2d[:, 1])
# 添加标签
for i, entity in enumerate(entities):
plt.annotate(entity, (entity_embeddings_2d[i, 0], entity_embeddings_2d[i, 1]))
plt.title('Entity Embeddings')
plt.show()
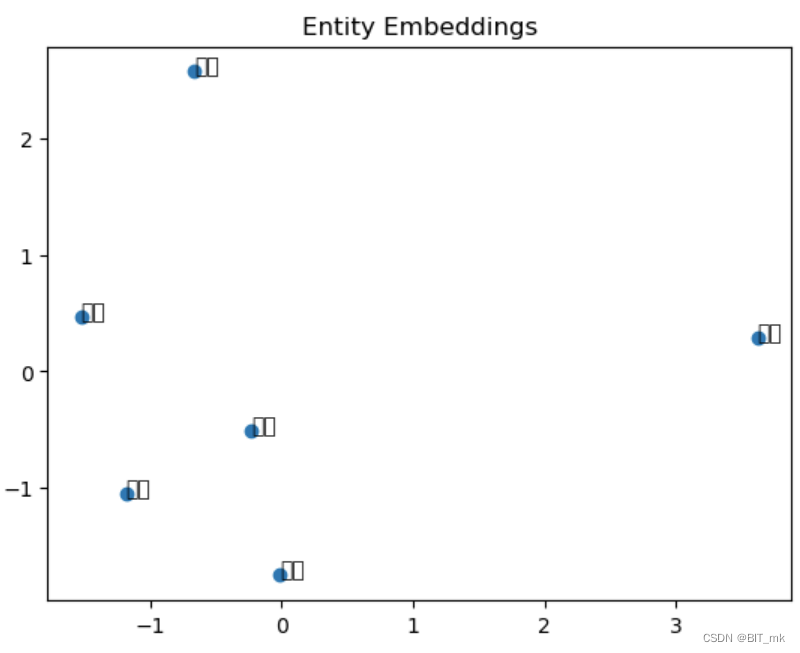
扩展:TransR , TransH and TransD
-
张量分解模型
RESCAL
RESCAL是一种用于知识图谱嵌入的张量分解方法。与许多其他知识图谱嵌入方法不同,RESCAL不是为每个关系学习一个单一的嵌入向量,而是为每个关系学习一个矩阵。这允许模型捕捉更复杂的关系,并可以更好地建模多对多关系。
RESCAL的工作原理
假设我们有一个三维张量,其中每个切片
表示一个关系,每个元素
表示实体
和
之间的关系
的存在或强度。
RESCAL通过以下方式分解这个张量:
- 实体嵌入:所有关系共享相同的实体嵌入矩阵
,其中每一行是一个实体的嵌入向量。
- 关系嵌入:对于每个关系
,RESCAL学习一个矩阵
。
- 重构:通过实体嵌入和关系矩阵,我们可以重构原始张量:
。
扩展:DistMult 、ComplEx
-
神经网络模型
这些方法应用多层非线性特征来计算实体和关系之间的交互作用,从而生成表达性特征嵌入。
TKG嵌入方法
根据要预测的时间戳,我们可以将这些方法分为两个背景:外推和插值
外推
外推模型侧重于预测未来时间戳t(t > tT)的新事实。他们通常通过将TKG视为事件序列来开发时间依赖的评分函数。
插值
目的是通过推断历史时间戳t(t0 <t<tT)中缺失的事实来补全TKG。这些工作通常为每个时间戳计算一个隐藏的表示,并扩展静态分数函数以利用时间信息。
具有语义属性的KG嵌入
在时间知识图嵌入中,关系及其涉及实体之间的语义属性仍未被探索。
方法

基于关系约束的评分函数
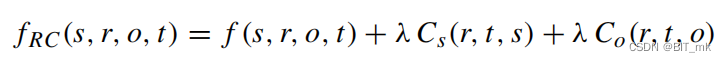
根据张量分解和超平面投影来设计评分函数。
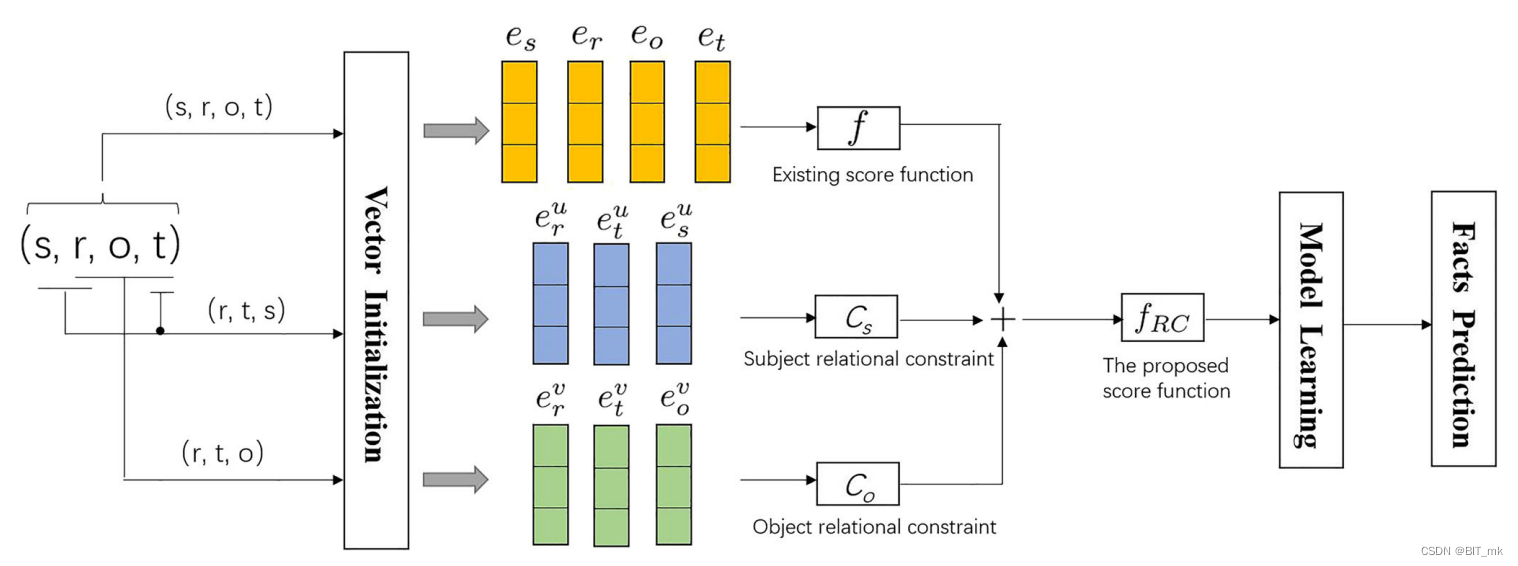
张量分解是一种广泛存在的变换函数,它可以通过将一个张量分解为分量秩1张量的和来计算一个元组的分数。
我们应用张量分解函数来模拟元组(r、t、s)和(r、t、o)的相互作用,并计算关系约束的值。
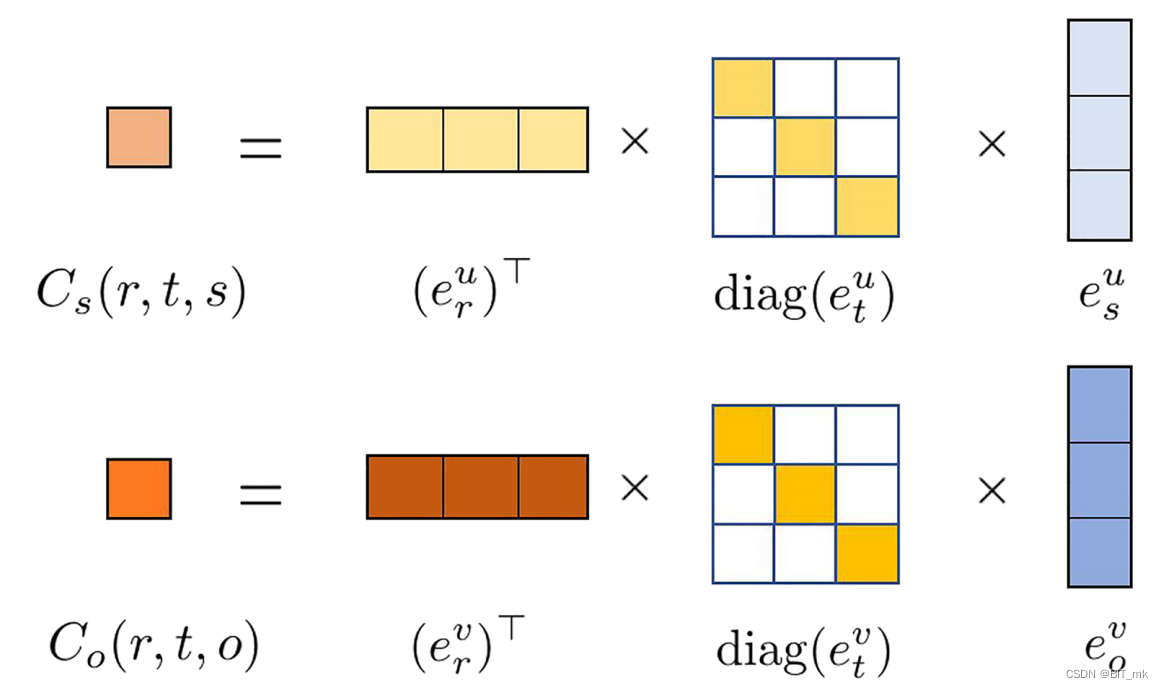
张量分解容易过拟合,所以引入正则化矩阵在对应的关系约束的元素。
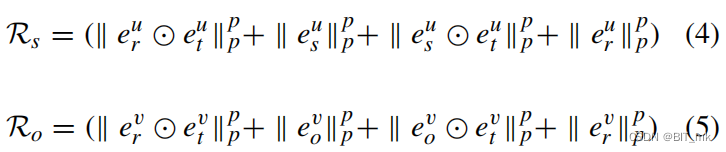
超平面投影:
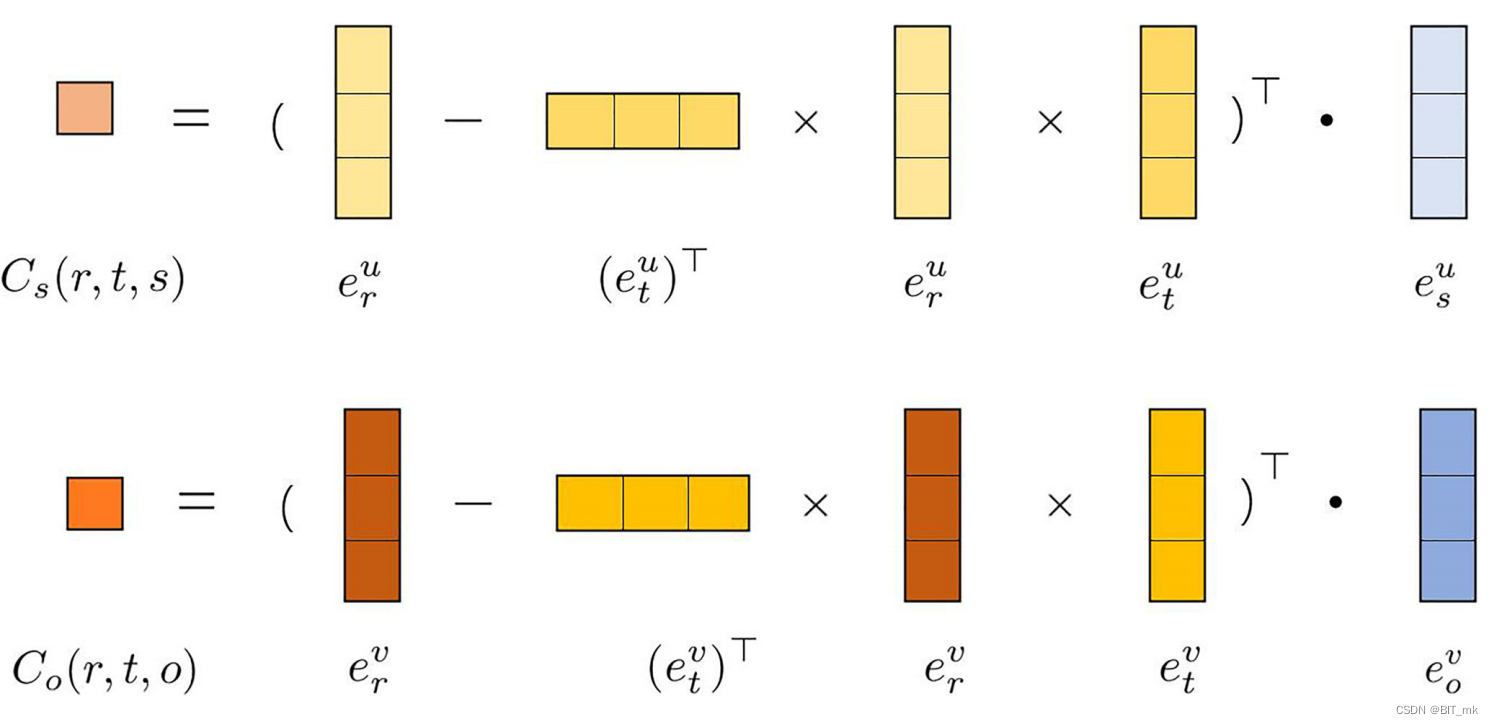

![[Linux]进程概念](https://img-blog.csdnimg.cn/img_convert/7584952d4714e8045fa13140f9e1b234.png)