用于步态识别的动态聚合网络
paper题目:Dynamic Aggregated Network for Gait Recognition
paper是BIT发表在CVPR 2023的工作
paper地址:链接
Abstract
步态识别有利于多种应用,包括视频监控、犯罪现场调查和社会安全等。然而,步态识别在实际场景中常常受到多种外部因素的影响,例如携带条件、穿着大衣、不同的视角等。近年来,各种基于深度学习的步态识别方法取得了可喜的成果,但它们往往使用固定权重的卷积网络来提取显着特征之一,没有很好地考虑关键区域步态特征之间的关系,并且忽略忽略了完整运动模式的聚合。在本文中,我们提出了一个新的观点,即实际步态特征包括多个关键区域的全局运动模式,并且每个全局运动模式由一系列局部运动模式组成。为此,我们提出了动态聚合网络(DANet)来学习更多有区别的步态特征。具体来说,我们在相邻像素的特征之间创建了一种动态注意机制,该机制不仅自适应地关注关键区域,而且还生成更具表现力的局部运动模式。此外,我们开发了一种自注意力机制来选择代表性的局部运动模式并进一步学习鲁棒的全局运动模式。对三个流行的公共步态数据集(即 CASIAB、OUMVLP 和 Gait3D)的广泛实验表明,所提出的方法可以对当前最先进的方法提供实质性改进。
1. Introduction
步态识别旨在远距离检索相同的身份,已广泛应用于社会治安[28]、视频监控[4、15、49]、犯罪侦查[25]等领域。与动作识别[17,53,54]和行人重识别[2,55,60,61]相比,步态识别是最具挑战性的细粒度标签分类问题之一。一方面,轮廓数据是受分割算法[26,62,63]的限制的人的二值图像,偶尔会有孔洞和破碎的边缘。另一方面,在真实场景中,步态识别也会受到各种外部因素的影响,如携带条件、穿着外套、不同的视角等。不同的角度和服装条件会极大地改变同一个人的剪影外观,导致类内差异远远大于类间差异。我们问:如何在各种外部因素的影响下,为每个人自适应地学习更稳健的特征?我们试图从以下几个角度回答这个问题:
(I)局部运动模式。步态,或行走的行为,本质上是身体各部分的协调运动。在步态序列中,我们观察到每个部分都有唯一的代表性运动模式,并且每个运动模式都由一组局部化子运动组成。因此,在各种外界因素的干扰下,准确定位判别部分,获得具有代表性的局部运动模式至关重要。然而,以前的基于步态的方法[7,8,13,14,20,24,33]简单地使用具有非线性激活的卷积网络来模拟动态运动。一旦网络被训练好,参数和非线性函数就只能集中在固定的模式上。为此,我们提出将每个像素的特征编码为具有幅度和相位的向量,如图1所示,这允许学习聚焦相邻像素之间的动态注意映射函数。通过对这种关系进行建模,网络可以进一步关注关键区域的局部运动模式。
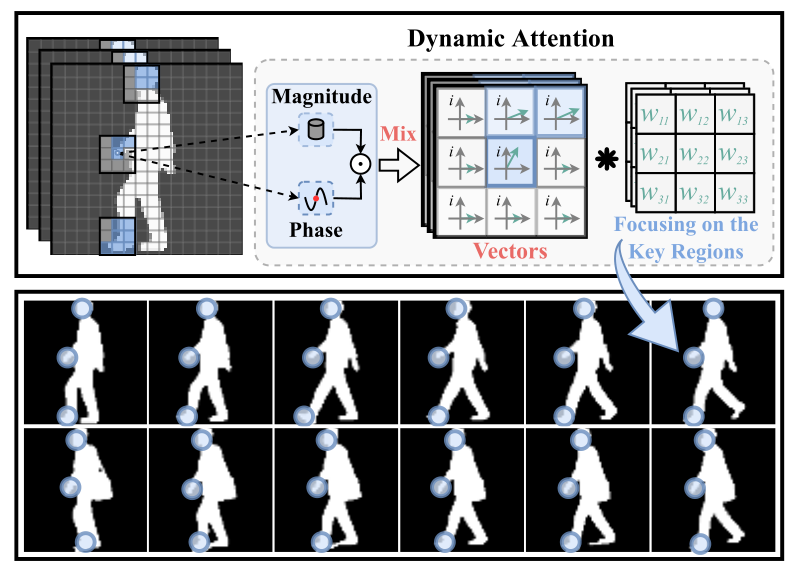
图1.每个像素的特征被映射为同时具有幅值和相位分量的矢量。幅值代表上下文信息,而相位分量用于构建关键区域的动态注意模型。卷积运算用∗表示,图中的蓝色圆圈表示动态注意力学习到的关键区域。
(Ii)全局运动模式。步态是一种周期性的运动。我们假设实际的运动模式是一维信号,如图2所示,其中局部运动模式是信号上的点。因此,有必要使用一系列局部运动模式来进一步拟合实际运动模式,以获得可区分的步态特征。然而,最近的基于步态的方法[8,20,33]只使用基于最大或平均的方法来提取其中一个重要的局部特征。这些方法容易受到干扰,不能适应实际的运动模式。根据信号处理理论中的Nyquist-Shannon采样定理[37,39],当以大于信号频率的两倍的频率对连续信号进行采样时,原始信号的信息保持不变。在这方面,我们提出构建一个全局注意模型,并使用它来动态地选择预设数量的可区分局部运动模式(绿色箭头),同时排除噪声(红色箭头)的影响。通过选择足够的区分局部运动模式,网络可以进一步获得稳健的全局运动模式。
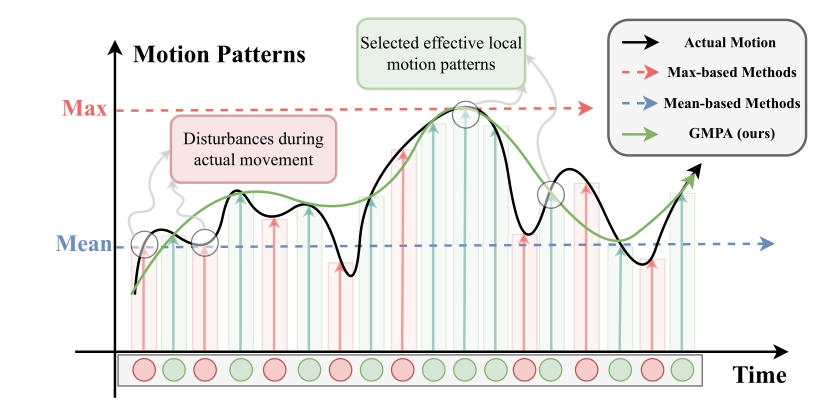
图2.实际运动模式与基于最大值的方法、基于均值的方法和全局运动模式聚合器(GMPA)模块的比较。黑色曲线表示受干扰影响的单个周期动作,而绿色曲线表示由GMPA选择的不同局部运动模式组成的合成周期动作。
在此基础上,提出了一种新颖有效的步态识别动态聚集网络(DANet)。如图3所示。DANet由两个设计良好的组件组成,即局部卷积混合块(LCMB)和全局运动模式聚合器(GMPA)。首先将每个像素的特征编码到包括幅度和相位的复数域中,其中幅度项代表上下文信息,而相位项用于建立每个向量之间的关系。通过聚集邻近焦点区域中的矢量的大小和相位来生成局部运动模式。其次,我们利用GMPA模型中的自注意机制动态地选择足够的可区分的局部运动模式,并进一步学习对实际步态模式的拟合。最后,使用我们提出的模型,我们获得了每个人最具代表性的稳定步态特征,并且性能优于最新的SOTA方法,特别是在最具挑战性的变装条件下。

图 3.提出的 DANet 概述。每个阶段都包含局部卷积混合块(LCMB),它利用动态注意力模型来建立感兴趣的相邻像素之间的关系。 HP表示水平池化,GMPA表示全局运动模式聚合器, l l l表示最后阶段的数量。特别地, G M P A j \mathrm{GMPA}_j GMPAj模块负责聚合第 j j j个部分的局部运动模式并产生最终的全局运动模式 v i ˉ {v}_{\bar{i}} viˉ以供识别。
本文的主要贡献如下:
-
提出了一种新的局部运动模式提取算法,该算法能够动态地对相邻像素的特征之间的关系进行建模,进而准确定位关键区域。
-
设计了一种有效的全局运动模式匹配算法,用于选择具有区分性的局部运动模式,并对其进行聚合以获得稳健的全局表示。据我们所知,在这项任务中探索自我注意模式的潜力是第一次尝试。
-
实验结果表明,该方法在CASIA-B[56]、OUMVLP[41]和Gait3D[59]数据集上的性能优于SOTA方法。此外,在CASIA-B[56]上的许多严格的消融实验进一步验证了DANet中每种成分的有效性。
2. Related Works
在这一部分中,我们简要概述了步态识别、局部动作建模和全局动作建模领域的相关研究。
步态架构。步态识别方法主要分为两个典型类别,即基于模型的方法和基于外观的方法。基于模型的方法 [1, 3, 27, 29–31, 44] 尝试将人体姿势结构 [10] 明确地拟合到图像。然而,预定义点是凭经验设计的,并受到低质量图像估计结果不准确的限制。因此,基于模型的方法在性能上通常不如基于外观的方法。基于外观的方法[7,8,13,18,20,21,24,32,33,43,47,51,52,58]是步态的主流框架,并受益于深度学习的快速发展。它大致可以分为三类,即基于模板的方法、基于集合的方法和基于序列的方法。基于模板的方法[18,36,43,47,52,57]通过压缩一系列步态轮廓(例如步态能量图像(GEI))来提取步态时空特征,这不可避免地破坏了判别性局部运动的表示步态序列中的模式。基于集合的方法[8,20,21,23]假设轮廓的外观包含其位置信息,这无法使用连续帧构建局部运动模式。最近一些先进的基于序列的方法[7,24,32,33,51]使用3D卷积(C3D)神经网络从步态序列中提取步态特征并实现SOTA结果。我们的方法属于基于序列的方法,与其他方法相比,我们提出使用可变长度帧作为输入。
局部动作建模。局部动作建模[14,24,32,33]旨在构建短程时空特征,这些特征已在各种文献中被证明有利于步态识别。 GaitPart [14]提出了一种微运动捕捉模块来建模短程时空特征。 MT3D [32]提出了多个时间尺度的 3D 卷积层来提取小和大时间尺度的运动特征。 GaitGL [33]利用局部时间聚合模块来提取局部时间信息。 3DLocal [24]提出了一个定位模块来自适应采样局部动作特征。与这些策略相反,我们提出将步态序列的每个像素映射到复值域,使用相位项来编码步态特征之间的关系。通过充分利用相位项,我们在特征的每个像素之间构建动态注意力模型,以提取关键区域的局部运动模式。
全局动作建模。旨在捕获远程依赖性的全局动作建模已被证明有利于广泛的识别任务,例如动作识别[6,45,48,54]和行人重识别[9,16,19, 35,40,61]。许多基于注意力的方法 [12,34,46] 在空间维度 [5, 50] 或通道维度 [22] 中建立了全局关系,并取得了显着的结果。然而,当前步态识别中最先进的工作[7,8,32,33]仍然直接使用基于Max或Mean的方法来提取全局时间特征,仅关注最显着的特征。与这些方法不同,我们设计了一个有效的全局自注意力模型来获得每个人的鲁棒表示,该模型可以选择有区别的局部运动模式,并进一步将它们映射到全局运动模式。
3. Methodology
在本节中,我们首先在第 3.1 节中描述我们方法的总体架构,然后介绍所提出的两个新颖的精心设计的模块,即第 3.2 节中的局部卷积混合块(LCMB)和第 3.3 节的全局运动模式聚合器(GMPA)。最后,我们将在 3.4 节中讨论联合损失函数。
3.1. Formulation and Motivation
步态识别旨在在各种外部因素的影响下识别同一个人。令 X ∈ R T × H × W \mathbf{X} \in \mathbb{R}^{T \times H \times W} X∈RT×H×W 表示包含连续 T T T 帧的轮廓数据,其中 T 、 H T、H T、H 和 W W W 表示时间,输入帧的高度和宽度尺寸。在我们的实现中,我们从连续序列中采样可变长度帧 T ∈ [ 20 , 40 ] T \in[20,40] T∈[20,40] 作为输入。步态特征的提取可表示为
f = G ( L ( X ) ) , f=\mathcal{G}(\mathcal{L}(\mathbf{X})), f=G(L(X)),
其中 f ∈ R P × C f \in \mathbb{R}^{P \times C} f∈RP×C是输出特征, P P P是水平切片部分的数量, C C C是特征通道, L \mathcal{L} L表示局部运动模式提取, G \mathcal{G} G表示全局运动模式聚合。
为了学习每个人的独特表征,之前基于 C2D 的方法 [8, 20] 和基于 C3D 的方法 [32, 33] 仅使用卷积层和非线性函数来学习步态特征。然而,经过训练的网络只能识别某些容易受到噪声影响的运动模式。在这项工作中,我们在 DANet 的主干中提出了一种新颖的 LCMB,它使网络能够专注于关键区域并通过动态构建像素之间的关系来提取局部运动模式。此外,受奈奎斯特香农采样定理[37, 39]的启发,我们提出了一个新的观点,即完整的步态模式应包含许多可区分的局部运动模式。为此,我们开发了一种有效的GMPA来选择足够可区分的局部运动模式,同时有效地排除噪声的干扰。然后聚合所选择的局部运动模式以生成鲁棒的全局运动模式。
3.2. Local Conv-Mixing Block
在本节中,我们详细描述了本地卷积混合块(LCMB)模块中的向量表示和向量聚合。
矢量表示。在 LCMB 模块中,输入特征表示为 V = [ v 1 , v 2 , … , v N ] ∈ R N × C i \mathbf{V}=\left[v_1, v_2, \ldots, v_N\right] \in \mathbb{R}^{N \times C_i} V=[v1,v2,…,vN]∈RN×Ci,其中 N N N是步态序列中的像素数, C i C_i Ci是输入特征的维度。如图4所示,我们得到幅度 ∣ v j ∣ \left|v_j\right| ∣vj∣和每个向量的相位 θ j \theta_j θj分别乘以可学习参数 W m ∈ R C i × C l W^m \in \mathbb{R}^{C_i \times C_l} Wm∈RCi×Cl和 W t ∈ R C i × C l W^t \in \mathbb{R}^{C_i \times C_l} Wt∈RCi×Cl,即
∣ v j ∣ = W m v j , j = 1 , 2 , ⋯ , N , θ j = max ( 0 , W t v j ) , j = 1 , 2 , ⋯ , N , \begin{gathered} \left|v_j\right|=W^m v_j, j=1,2, \cdots, N, \\ \theta_j=\max \left(0, W^t v_j\right), j=1,2, \cdots, N, \end{gathered} ∣vj∣=Wmvj,j=1,2,⋯,N,θj=max(0,Wtvj),j=1,2,⋯,N,
其中下标 j j j是第 j j j个像素的特征。每个向量的内容是由幅度项 ∣ v j ∣ \left|v_j\right| ∣vj∣ 建模的实值特征,而每个向量的关系由相位项 θ j \theta_j θj 进行调制,使用具有修正线性的分组卷积层激活 ReLU。复向量 v ~ j ∈ C C l \tilde{v}_j \in \mathbb{C}^{C_l} v~j∈CCl 使用欧拉公式通过幅度和相位项进行调制,即:
v ~ j = ∣ v j ∣ ⊙ cos θ j ⏞ real part + i ∣ v j ∣ ⊙ sin θ j ⏞ imaginary part , j = 1 , 2 , ⋯ , N , \tilde{v}_j=\overbrace{\left|v_j\right| \odot \cos \theta_j}^{\text {real part }}+\overbrace{i\left|v_j\right| \odot \sin \theta_j}^{\text {imaginary part }}, j=1,2, \cdots, N, v~j=∣vj∣⊙cosθj real part +i∣vj∣⊙sinθj imaginary part ,j=1,2,⋯,N,
其中 i i i是满足 i 2 = − 1 i^2=-1 i2=−1的虚数单位, ⊙ \odot ⊙是逐元素乘法。
向量聚合。将每个像素的特征表示为向量后,我们进一步聚合每个向量的局部时空域,如图4所示。特别是,由可学习的卷积核 K ∈ R C i × C l × K t × K s × K s \mathcal{K} \in \mathbb{R}^{C_i \times C_l \times K_t \times K_s \times K_s} K∈RCi×Cl×Kt×Ks×Ks聚合的输出 o ~ j ∈ C C i \tilde{o}_j \in \mathbb{C}^{C_i} o~j∈CCi的复值表示,即
o ~ j = ∑ m ∈ N ( j ) K [ j − m ] v ~ m + v j , j = 1 , 2 , ⋯ , N , \tilde{o}_j=\sum_{m \in \mathcal{N}(j)} \mathcal{K}[j-m] \tilde{v}_m+v_j, j=1,2, \cdots, N, o~j=m∈N(j)∑K[j−m]v~m+vj,j=1,2,⋯,N,
其中 N ( j ) \mathcal{N}(j) N(j)表示 j j j的相邻像素集, v ~ m \tilde{v}_m v~m表示属于 v ~ j \tilde{v}_j v~j的相邻像素的向量。按照[42],为了方便计算,我们通过将 v ~ j \tilde{v}_j v~j的实部和虚部相加来获得实值输出特征 o j ∈ R C i o_j \in \mathbb{R}^{C_i} oj∈RCi,即:
o j = ∑ m ∈ N ( j ) ( K [ j − m ] ∣ v m ∣ ⊙ cos θ m + K [ j − m ] ∣ v m ∣ ⊙ sin θ m ) + v j , j = 1 , 2 , ⋯ , N , \begin{aligned} & o_j=\sum_{m \in \mathcal{N}(j)}\left(\mathcal{K}[j-m]\left|v_m\right| \odot \cos \theta_m+\right. \\ & \left.\mathcal{K}[j-m]\left|v_m\right| \odot \sin \theta_m\right)+v_j, j=1,2, \cdots, N, \end{aligned} oj=m∈N(j)∑(K[j−m]∣vm∣⊙cosθm+K[j−m]∣vm∣⊙sinθm)+vj,j=1,2,⋯,N,
其中 ( cos θ m + sin θ m ) \left(\cos\theta_m+\sin\theta_m\right) (cosθm+sinθm)表示 j j j的相邻像素之间的动态注意力。为了进一步理解动态聚合模型,显示相位值的热图如图 6 所示。
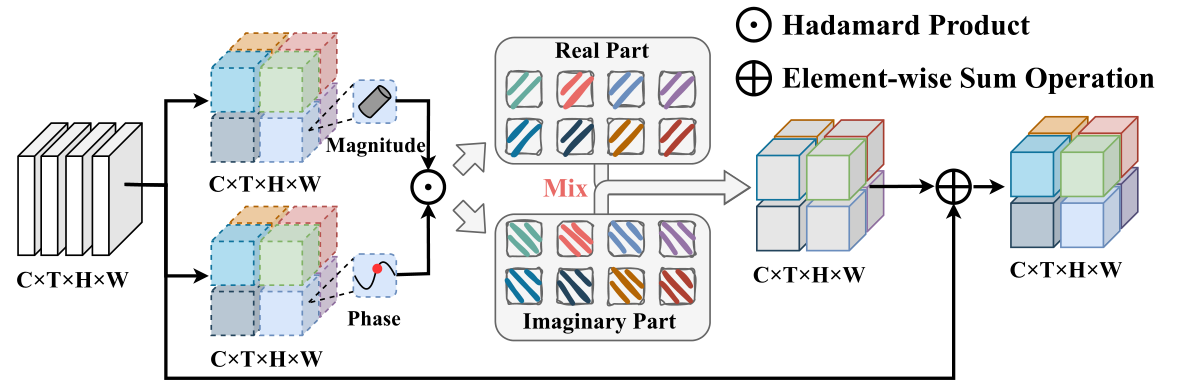
图 4. LCMB 的架构,其中“⊙”表示 Hadamard 乘积,“⊕”表示逐元素求和运算,Mix 表示向量聚合运算。

图 6. 同一人剪影中相位值和相应位置(实心点)的注意力图(虚线框)可视化,其中“J”代表脸部,“H”代表手,“L”代表腿,“F”代表脚。
3.3. Global Motion Patterns Aggregator
在这一部分中,我们提出了一种用于步态识别的全局动作建模框架的新实例,称为全局运动模式聚合器(GMPA),它选择预设数量的区分局部运动模式,然后利用注意机制来聚合查询特定的全局运动模式每个查询位置。 GMPA 对每个部分采用单独的参数,并对相应部分的全局运动模式进行建模。
低阶全局运动模式。步态数据受到许多可变因素的影响,例如分段孔或破损边缘,进一步损害实际的运动模式。为此,我们首先提出将可变的局部运动模式压缩到预设数量的通道描述符中。然后,我们利用softmax在时间维度上构建注意力图,并将压缩的注意力图与重塑的局部运动模式特征相乘以获得全局低阶运动模式。形式上,全局低阶运动模式
G
~
∈
R
P
×
C
×
M
\tilde{\mathbf{G}} \in \mathbb{R}^{P \times C \times M}
G~∈RP×C×M由局部运动模式
L
∈
R
P
×
T
×
C
\mathbf{L} \in \mathbb{R}^{P \times T \times C}
L∈RP×T×C和注意力图
M
∈
R
P
×
T
×
M
\mathbf{M} \in \mathbb{R}^{P \times T \times M}
M∈RP×T×M生成,并且可以表示为
M
=
exp
(
W
1
L
i
)
∑
i
=
1
T
exp
(
W
1
L
i
)
,
G
~
=
M
⊗
L
,
\begin{gathered} \mathbf{M}=\frac{\exp \left(W_1 \mathbf{L}_i\right)}{\sum_{i=1}^T \exp \left(W_1 \mathbf{L}_i\right)}, \\ \tilde{\mathbf{G}}=\mathbf{M} \otimes \mathbf{L}, \end{gathered}
M=∑i=1Texp(W1Li)exp(W1Li),G~=M⊗L,
其中
W
1
∈
R
P
×
C
×
M
W_1 \in \mathbb{R}^{P \times C \times M}
W1∈RP×C×M是Separate
F
C
1
的权重,
i
F C_1的权重,i
FC1的权重,i是帧的索引,
⊗
\otimes
⊗表示矩阵乘法。
高阶全局运动模式。为了利用低阶全局运动模式中聚合的信息,我们进行了进一步的映射,旨在完全捕获高阶全局运动模式。此外,我们还将残差学习引入到 GMPA 中以简化训练。具体来说,我们进一步将预设数量的低阶全局运动模式 G ~ \tilde{\mathbf{G}} G~映射为高阶全局特征 G \mathbf{G} G,即
G = δ ( W 2 G ~ ) ⊕ L , \mathbf{G}=\delta\left(W_2 \tilde{\mathbf{G}}\right) \oplus \mathbf{L}, G=δ(W2G~)⊕L,
其中 W 2 ∈ R P × M × 1 W_2 \in \mathbb{R}^{P \times M \times 1} W2∈RP×M×1是Separate F C 2 的权重, δ F C_2的权重,\delta FC2的权重,δ表示LeakyReLU激活函数, ⊕ \oplus ⊕表示逐元素广播添加。
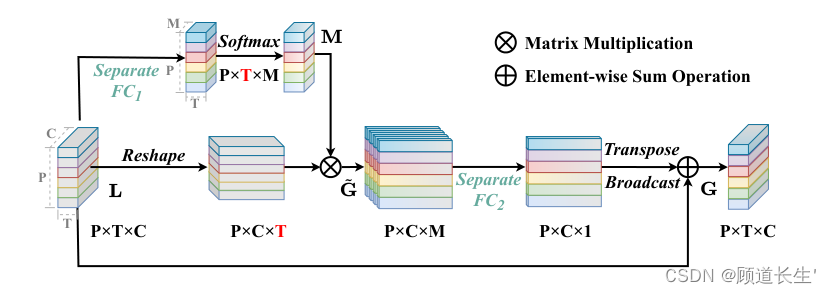
图 5.GMPA 的架构和特征图按维度显示,其中“⊗”是矩阵乘法。